Systematic attribution of heatwaves to the emissions of carbon majors

Definition of events

From the EM-DAT database, we select the events only after 2000, because the reporting is more complete after this date25,50, and since climate change has been shown to exert increasing influence on extremes over this period51.

The locations reported for the events in the EM-DAT database are names of cities, provinces, states or whole countries (for example, France). Geographical boundaries are necessary for the analysis, so the locations of EM-DAT are matched to spatial elements from GADM52 using the following algorithm.

1.

The reported ISO code is used to pre-select the spatial elements of GADM for the country and any attached disputed territories.

2.

The reported location is prepared: replacing spatial characters (accents, numbers and punctuation); removing extra spaces; lowercase letters for all characters; synthesizing specific sentences (for example, ‘Kadamjay district in Batken oblast’ becoming ‘Kadamjay’); correcting for any change in regional aggregation (for example, ‘Haute & Basse Normandie’ becoming ‘Normandie’); translating any region without its variant in GADM (for example, ‘Voreio Aigaio’ becoming ‘North Aegean’).

3.

Each preselected spatial element is compared with each element of the prepared reported location by applying a character matcher53 on its names and variants.

4.

Each retained spatial element is filtered using a prepared list of false positives. For instance, the location for the state of ‘Ohio’ triggers the identification of the county ‘Ohio’ in the states of Kentucky and West Virginia, which have not been reported.

5.

The list of spatial elements is compared with the initial reported location, checking whether it matches correctly. If not, the issue is implemented through the prepared lists of known issues in steps 2 and 4.

Another work, the dataset GDIS, is also used to match EM-DAT locations to geographical boundaries54. Both approaches have been developed independently. GDIS differs in that the locations of all categories of hazards are analysed, but only up to 2018. Here, only the hazards for heatwaves were analysed, but up to 2023. Moreover, GDIS uses GADM v.3.6, whereas our work uses GADM v.4.1.

In the EM-DAT database, the dates of the heatwaves are often reported with the starting and ending days. When both days are provided, we use the average of the daily average temperature over this exact period. Other indicators may be possible26, but the average aggregates the essential features of these heatwaves55. In particular, this choice is motivated by its relevance for the reported impact rather than its meteorological rarity. Heatwaves affect local populations not only through daily maximum temperatures but also through lack of cooling at night, which can be estimated using daily average temperatures. Sustaining high temperatures over time modifies the impact of a heatwave as well, justifying the use of averages over the period of the heatwave rather than its peak. The annual indicator is calculated first on each grid point, then averaged over the defined region to maximize the relevance of the indicator1,56. Furthermore, some events were reported without the starting and/or ending day(s). We observe that heatwaves reporting both days and lasting less than a month last on average for 8 days. Therefore, we use as an indicator for events with missing days the maximum of the 8 days running average over the reported month. In the case that several months were reported with missing starting and/or ending days, we lengthen the duration of the running average by 1 month for each supplementary month reported.

Training of conditional distributions

The statistical model of attribution studies is carefully chosen to model the frequencies and intensities of extreme events1,56. To capture possible trends and non-stationarities, the distribution depends on the parameters driven by explanatory variables. In this study, we opt for the generalized extreme value (GEV) distribution with a linear evolution of its location as outlined in equation (1). For every year y in the sample, the average temperature over the period and region of the event Ty is assumed to follow a GEV distribution of location μ, scale σ and shape ξ, whereas the location varies with the change in global mean surface temperature smoothed over the 3 previous years (GMST).

$$T \sim \mathrm{GEV}(\mu ={\mu }_{0}+{\mu }_{1}\mathrm{GMST},\sigma ={\sigma }_{0},\xi ={\xi }_{0})$$

(1)

Although the statistical model in equation (1) is common for the EEA of heatwaves1,56, we have compared its performance with other potential models. Apart from this GEV model, we have tested three other distributions with linear and non-linear evolutions of the parameters: Gaussian, skew normal and generalized Pareto. Overall, our comparisons assessed through quantile–quantile plots indicate that the GEV performs the best among the four distributions, especially in terms of upper tail behaviours. We calculate the classical Bayesian information criteria (BIC) to compare their performances while reducing the risk of over-fitting57. We observe that for all heatwaves, a stationary GEV has the lowest BIC. We note that the linear model of equation (1) is not always the best distribution according to the BIC, although the gain in BIC from the linear model to the best solution is always marginal. More quantitatively, the improvement in BIC from the stationary GEV to the linear model represents between 88% and 100% of the improvement from the stationary model to the best solution over all heatwaves analysed, with an average of 98%. In other words, sophisticating further the statistical model would, on average, improve the performance by only 2%. This result confirms that this expression is the most appropriate for most heatwaves.

These fits are obtained by minimization of the negative log likelihood (NLL) of the training sample58. The first guess has its robustness improved using initial regression to approximate the coefficients42,59. The shape parameter is bounded between −0.4 and 0.4 (ref. 1). Moreover, the sample is weighted during minimization of the NLL, with weights equal to the inverse of the density of the GMST. This approach helps in providing equal performance over the full interval of GMST.

The choice of whether to include the event or not when estimating the statistical model has been extensively discussed, although no final consensus has been reached1,31,60. The results presented in this paper have been obtained by estimating the event, to prevent removing points from the observational record. To ensure numerical convergence, a minimum probability of 10−9 was set for each point of the full sample. It implies that the attributed events under factual conditions will not have return periods higher than a thousand million years, which we consider long enough.

Estimating return periods for unlikely events with relatively short observational records remains difficult34; thus, we append additional lines of evidence1,56. Conditional distributions are trained for ERA5, used as reference, but also with BEST29 (Extended Data Fig. 1) and simulations from Climate Model Intercomparison Phase 6 (CMIP6)30,61. The following Earth system models (ESMs) from CMIP6 are used: ACCESS-CM2, ACCESS-ESM1-5, AWI-CM-1-1-MR, BCC-CSM2-MR, CESM2, CESM2-WACCM, CMCC-CM2-SR5, CMCC-ESM2, CanESM5, EC-Earth3, EC-Earth3-CC, EC-Earth3-Veg, EC-Earth3-Veg-LR, FGOALS-g3, GFDL-CM4, GFDL-ESM4, INM-CM4-8, INM-CM5-0, IPSL-CM6A-LR, KACE-1-0-G, KIOST-ESM, MIROC6, MPI-ESM1-2-HR, MPI-ESM1-2-LR, MRI-ESM2-0, NESM3, NorESM2-LM, NorESM2-MM and TaiESM1. For every heatwave, only the ESMs with sufficient performance are used, as described in the next section. For ERA5 and BEST, we start the time series in 1950 for adequate spatial coverage over all regions62, and these time series finish in 2022 for BEST and 2023 for ERA5. For CMIP6, the time series is calculated over the historical (1850–2014) (ref. 63) and the SSP2-4.5 (2015–2100) (ref. 64). This scenario is chosen because its emissions are the closest to those observed over 2015-202 (ref. 36). Only runs with the initial conditions termed r1i1p1f1 are used, as it was run by most ESMs. Only one ensemble member is used to facilitate the comparison of the parameters and probabilities from ESMs to those based on observations.

Evaluation of the uncertainties

During the extreme event analysis, two sources of uncertainties are handled—namely, on the conditional distributions and on the handling of observations and simulations.

During the training of conditional distributions, the uncertainties on the parameters are obtained using an ensemble of 1,000 bootstrapped members, with replacements allowed during the resampling. The conditional distributions are then used to assess the probabilities and intensities of the event, under a factual climate and a counterfactual climate. The factual climate is defined as the GMST observed at the time of the event. The counterfactual climate is defined as the average of the GMST over 1850–1900.

ESMs exhibit different performance in reproducing local climates; thus, not all models may be useful for event attribution1. We calculate the seasonalities of ERA5 and each ESM over 1950–2020 in each grid point over the region. We then average their correlation. The most appropriate ESMs are the 10 most representative ESMs that maximize this average correlation.

Following the WWA approach, not all models are retained for further analysis1,65. The factual distributions at the time of the event are compared with those of ERA5. Both the scale and the shape parameters of ERA5 and the model must have their 95% confidence intervals overlapping. Otherwise, the model will be discarded. Thus, the overall selection process is to sort the ESMs by correlation with ERA5 seasonality, remove those with parameters inconsistent with ERA5 and select the 10 best ESMs in this list.

At this point, probability ratios and change in intensities are obtained for an ensemble of datasets, each with uncertainties. To synthesize over this large ensemble, equal weights are given to each bootstrap member of ERA5 and BEST, summarized into one distribution for observations. All kept ESMs are also given equal weights and summarized into one distribution for models. Finally, these distributions are averaged to deduce the median and 95% confidence intervals. We point out that synthesizing these lines of evidence could be conducted with other approaches1, although without affecting the main messages of this work.

Goodness of fit for the conditional distributions

Although using a non-stationary GEV with its location varying linearly with GMST is a well-established approach for EEA to statistically model extremes under global warming, this setup may not be well-suited in isolated cases66. To ensure that the GEV model represents the data adequately, the goodness of fit is verified for each conditional distribution used in this analysis with the method used in ref. 67.

For every heatwave, several datasets are used for analysis, from which conditional distributions are fitted. The location and scale of each of these fitted conditional distributions are used to transform the respective training sample onto a stationary GEV(0, 1, ξ) with the same shape as the fitted conditional distribution. This transformed sample has observed quantiles, which are compared with the theoretical quantiles of a GEV(0, 1, ξ) in a quantile–quantile plot. This quantile–quantile plot describes how well the GEV model describes the sample. The uncertainty in the GEV parameters determines a confidence band in the quantiles around the identity line, as shown in Extended Data Fig. 2.

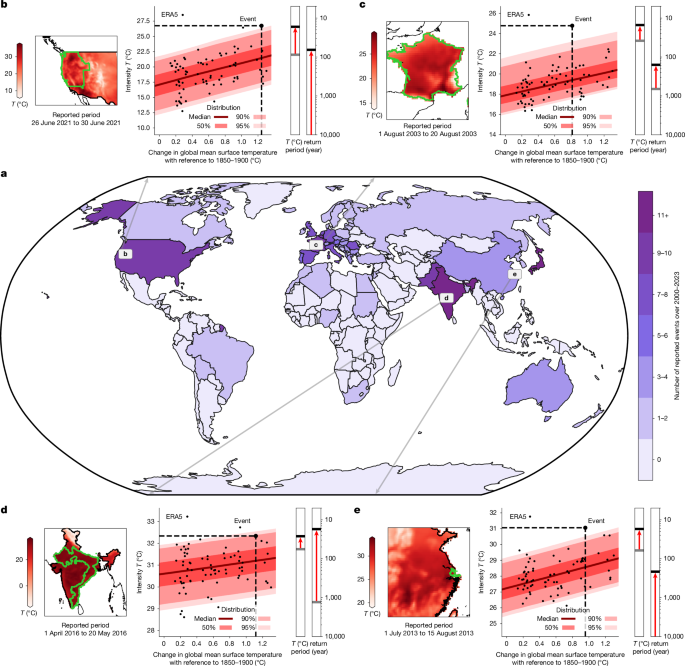
The fraction of the sample out of the confidence band is deduced, estimated as a 95% confidence interval on the ensemble obtained from bootstrapping of the training of the conditional distribution. For each heatwave, the ensemble of conditional distributions is compared with an out-of-sample threshold at 5%. The results are shown in Extended Data Fig. 3. If the median out-of-sample fraction across the conditional distributions is below the threshold, the goodness of fit is confirmed, and the heatwave is kept for the ensuing analysis. As shown in Extended Data Fig. 3, 217 heatwaves are retained, and nine are removed from the ensuing analysis. These nine events removed from analysis are summarized in Extended Data Table 1.

Out of the nine events, eight occurred in India, and the last one occurred in Japan. In the 217 heatwaves kept for analysis, eight events occurred in India. Besides this apparent regional clustering, no discernible traits emerge with regard to the season or length of the heatwave. More research is required to investigate why these fits do not perform as well as elsewhere for these specific events, which lies beyond the scope of this study.

Causality using Granger causal inference

The well-established approach1 for EEA combines observations and simulations by using non-stationary distributions. These distributions correlate the evolution of the climate indicator T for the heatwave to GMST. Deducing causality, that climate change caused the event, using this correlation relies on the strong physics-based understanding5,6,31,41,65,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97 that increasing GMST tends to also increase regional temperatures, not only through its mean but also through the whole distribution inferred from natural variability, thus shifting the regional extremes as well. Yet, although there is a strong physical basis for this causality, we can also investigate the validity of this causality from a statistical perspective. Using Granger causal inference98, we may assess the predictive relationship between GMST and T, the climate indicator of the event4.

The common approach for Granger causality4,98 requires that the input variables are stationary to train vector auto-regressive models99. This is usually verified by differentiating the variables, in other words, taking the interannual variability. This method would then assess whether the interannual variability of GMST can predict the interannual variability of T, thus focusing on the predictability of short-term shocks. However, the trend contains a stronger signal compared with the interannual variability. To account for long-term trends in GMST and T, Granger causality can be generalized using the vector error correction model (VECM)100. It requires the search for an adequate VECM model based on the Akaike information criterion101 and a co-integration test, for instance, using a Johansen test99. Nevertheless, this method still fails to account for non-linear effects. An alternative is to use machine learning, such as Random Forest models trained to predict T with GMST through their lagged effects102. Permutation tests are conducted to assess the performance of Random Forest models trained on permuted lagged GMST, compared with the non-permuted version103. Applying this method accounts for the evolution of GMST and T, while also accounting for non-linear effects.

By using the latter method, only three events have a median value for the test above 0.05. As shown in Extended Data Fig. 4, for 214 events out of 217, we reject the null hypothesis, concluding that the evolution of GMST is Granger-causing the evolution of T. The three other events are listed in Extended Data Table 2. We notice that the median value for the Granger causality remains relatively low. Using IPCC terms, it is likely (>66%) that GMST Granger-caused the evolution of T for the event in the United States in 2011, whereas it is very likely (>90%) for all the others. These three events are removed from this analysis.

Contributions from the carbon majors to global warming

The contributions of emissions of the carbon majors to global mean surface temperature are assessed with the reduced-complexity Earth system model OSCARv3.3 (refs. 104,105). The model embeds an ensemble of modules that replicate the behaviour of models of higher complexity105. OSCAR features the ocean and land carbon cycles with a bookkeeping module for CO2 emissions from land use and land cover change, wetlands, permafrost, tropospheric and stratospheric chemistry, and global and regional climate responses to these forcers. It accounts for the effects of greenhouse gases (CO2, CH4, N2O and 37 halogenated compounds), short-lived climate forcers (stratospheric water vapour, tropospheric and stratospheric ozone, primary and secondary organic aerosols, nitrates, sulfates and black carbon), surface albedo change, volcanic activity, solar radiation and contrails37,105.

OSCAR is run over the historical period (1750–2023), following three sets of simulations: (1) The first set of simulations is driven by concentrations of greenhouse gases to ensure a match with the latest observations. (2) The second set is driven by emissions, using the compatible emissions from the first set obtained through mass balance106,107. This is a control run that confirms that the estimated compatible emissions lead to the observed atmospheric concentrations and is used as a reference for the following attribution runs. (3) In the third set of simulations, for each carbon major, the control run is repeated, but the CO2 and CH4 emissions of the major are subtracted from the compatible emissions. The difference in outcome (for example, global temperature) between the control and this simulation gives the contribution of the major. This approach is called a residual attribution method108.

In all simulations, the radiative forcings from species or forcers that are neither CO2 nor CH4 (that is, forcers that are not attributed in this study) are prescribed as global time series based on the latest version of the Indicators of Global Climate Change35. Global time series of atmospheric concentrations for the first set of simulations come from the same source. Emissions of short-lived species (that affect the atmospheric sink of CH4) are taken from the latest version of the CEDS dataset109,110 and the updated GFED4s dataset111 that extends the original CMIP6 emissions from biomass burning112. Land use and land cover change data are the same as in the latest Global Carbon Budget36, in which we use both an updated LUH2 dataset113 and the FAO-based dataset114.

OSCAR runs in a probabilistic framework to represent the uncertainty in the modelling of the Earth system. This uncertainty is sampled through a Monte Carlo approach with n = 2,400 elements. The uncertainty in the natural processes governing the atmospheric concentration of CO2 and CH4 comes from the available parametrizations of OSCAR105,115,116. The uncertainty in the input radiative forcing follows that of the IPCC AR6 (ref. 117) and is applied uniformly to the whole time series. The uncertainty in the input land use and land cover change is sampled by running one-half of the simulations with one dataset and the other half with the other dataset. There is no uncertainty in the input emissions. Finally, the raw uncertainty range from the Monte Carlo is constrained with observational data by weighting the elements of the ensemble based on their distance to the observations in the control simulations37,116. As constraining values, we use decadal CO2 emissions from fossil fuels and industry over 2012–2021 from the GCB36, decadal anthropogenic CH4 emissions over 2008–2017 from the AR6 (ref. 118) offset with their preindustrial value from PRIMAP third-party-based estimates119,120, and decadal global mean surface temperature change over 2011–2020 from the AR6 (ref. 9).

Contributions from the carbon majors to heatwaves

We assess whether the probability can be written as a sum of terms, with each term associated with contributions from anthropogenic actors or natural drivers.

We define a region in space S. Every year y, the temperature field over the region is averaged over a period p of the year, then over the region S, resulting in the temperature Ty. The heatwave is characterized by the exceedance of the heatwave level u by Ty, with u a real-valued scalar. Ty represents a real-valued continuous random variable (Borel σ-algebra on the reals). Given the heatwave level u, the target probability is a survival function P(Ty > u).

We assume that the probability of the heatwave is conditional on GMTy and that it follows the statistical model introduced in equation (1) and represented in equation (2). Every year, the temperature over the region and the period Ty is sampled from a non-stationary GEV distribution27. The parameters of this GEV distribution are the location μ, the scale σ and the shape ξ. The location varies linearly with a covariate, the change in GMSTy at the corresponding year.

$$P({T}_{y} > u|{\text{GMST}}_{y})=1-\text{GEV}(u|\mu ={\mu }_{0}+{\mu }_{1}\text{GMT},\sigma ={\sigma }_{0},\xi ={\xi }_{0})$$

(2)

With the analytical expression for the cumulative distribution function of the GEV that follows equation (3):

$$\text{GEV}(u|0,1,\xi )=\left\{\begin{array}{c}\exp (-{(1+\xi u)}^{-1/\xi })\,\text{for}\;\xi \ne 0\,\text{and}\,1+\xi u > 0\\ \exp (-\exp (-u))\,\text{for}\;\xi =0\end{array}\right.$$

(3)

This well-established statistical model is widely used for EEA1,56 and has already been used extensively for heatwaves. We acknowledge that a more sophisticated model with additional covariates may further improve the performance121,122. However, this statistical model has been shown to have good performance for heatwaves in general13, and additional covariates can prevent the use of climate models as additional lines of evidence. The former section provides additional grounds for the choice of this model.

The causal theory applied to climate change justifies the decomposition of probabilities in a Gaussian case123,124. Given a statistical model built on a non-stationary Gaussian distribution linearly driven by GMST, if GMST can be split into a sum of contributions, then the probabilities can be approximated as a sum of their associated contributions123,124. However, the statistical model presented in equation (2) uses a GEV instead of a Gaussian. Even by attempting to write the decomposition using Bayes’s theorem and the inclusion–exclusion principle, the exact analytical form of each term remains challenging. This is mostly because the differences in probability when removing a contribution to GMST depend on the initial value of GMST. In other words, the non-linearity and the high number of terms lead to a solution that cannot be computed exactly.

Instead, we propose to approximate the solution and to investigate the quality of this approximation. The usual approach to calculate contributions to climate change is to run the statistical model with all contributors, then to run it again without one contributor, the difference corresponding to the contributor. This approach is thereafter called All-But-One (ABO). Thus, an emitter e with a contribution to global warming GMSTy,e would contribute to the probability of the event using this approach.

$${P}_{y,e}^{\text{ABO}}=P({T}_{y} > u|{\text{GMST}}_{y})-P({T}_{y} > u|{\text{GMST}}_{y}-{\text{GMST}}_{y,e})$$

(4)

To account for non-linear effects in the decomposition of probabilities, this approach is complemented with a second approach that calculates the difference in GMSTy introduced by adding only the emitter (Add-One-to-None, AON). According to this approach, the emitter e would contribute to the probability of the heatwave as follows:

$$\begin{array}{c}{P}_{y,e}^{\text{AON}}=P\left({T}_{y} > u|{\text{GMST}}_{y,e}\,+\,{\text{GMST}}_{y}-\sum _{e}{\text{GMST}}_{y,e}\right)\\ \,-\,P\left({T}_{y} > u|{\text{GMST}}_{y}-\sum _{e}{\text{GMST}}_{y,e}\right)\end{array}$$

(5)

The approach based on the removal of a single entity (ABO) estimates the contribution of a state perturbed by all the other contributors. The approach based on the addition of a single entity (AON) evaluates the contribution in an unperturbed state, without the other contributors interfering. Given the non-linearity of the system, we expect the physical contribution to be between the two values. We choose to calculate both approaches and average them. This approach, calculated using equation (6), is called the combined ABU & AON (Extended Data Fig. 5).

$${P}_{y,e}=\frac{{P}_{y,e}^{\text{ABO}}+{P}_{y,e}^{\text{AON}}}{2}$$

(6)

For each event, the probability is calculated for all datasets for the region and averaged over the datasets. Its 95% confidence interval is calculated using bootstrapping. The total probability of the event is decomposed into contributions of each carbon major, other climate forcers and preindustrial probability. After decomposition, these terms are summed up for comparison with the total probability. The 95% confidence interval is shown for all events, and only one event (Cyprus, May–September 2022) does not reproduce the total probability. This event has been removed from the analysis of extreme events. As shown in Extended Data Fig. 5, the average of ABO and AON provides the best estimate, because it accounts for non-linear effects.

In EEA, probabilities are often communicated using probability ratios, quantifying how many times climate change has made the event more likely. It is calculated using the probability of the event in a preindustrial climate, thus with a GMST averaged over 1850–1900:

$$\text{PR}\,=\,\frac{P({T}_{y} > u|{\text{GMST}}_{y})}{P({T}_{y} > u|{\text{GMST}}_{1850\mbox{–}1900})}$$

(7)

Because the contribution of the emitter e to the probability of the heatwave Py,e is a perturbation, the emitter multiplies the probability of the heatwave as in equation (8):

$${\text{PR}}_{e}=1+\frac{{P}_{y,e}}{P({T}_{y} > u|{\text{GMST}}_{1850\mbox{–}1900})}$$

(8)

Discussing an alternative decomposition approach

Alternatively to the approach based on GMST, a basic approach would be to assess the contributions directly with the emissions. The fraction in the cumulative emissions at the time of the event would represent the share of responsibility of the carbon major in the causes of the event. This fraction can be used for the change in intensity and the change in probability of the event. This approach can be compared with the principle applied for the attributional life cycle assessments, taking the Earth system as a whole and using the shares in its inputs to trace the perturbation125,126, whereas the approach based on GMST traces the effects of the carbon majors through the Earth system. Therefore, GMST is more similar to the principle of the consequential life cycle assessment. However, the approach based on cumulative emissions has several drawbacks.

First, the carbon majors fuel climate change with CO2 and other compounds, such as CH4. As an approximation, it would still be possible to aggregate these compounds using a global warming potential for fossil CH4.

Then, the carbon cycle partially absorbs the emitted carbon over time. Thus, two companies with the same cumulated emissions may not share the same responsibility, if one has older emissions, thus with a lower contribution to the atmospheric concentration of CO2. Still, these old emissions contributed to warming up the Earth system and saturating the carbon sinks.

Finally, the attribution analysis may not respond linearly to changes in GMST. For our study, heatwaves are represented with a GEV with the location varying linearly with GMST. According to the Transient Climate Response to Emissions (TCRE), the GMST varies almost linearly with cumulative emissions. Thus, the approach based on cumulative emissions would lead to similar results to ours. However, for events for which the distributions do not vary linearly with GMST, as it may for extreme precipitations1,56, non-linearities would be introduced.

To conclude, the approach based on cumulative emissions is an approximation that relies on the linearity of the Earth system. However, this system is not entirely linear, and the TCRE is known as an approximation with its limits127. Under the assumptions that the linearity of the system would be respected, this simple approach would then lead to similar results as those based on the approach used in this work.