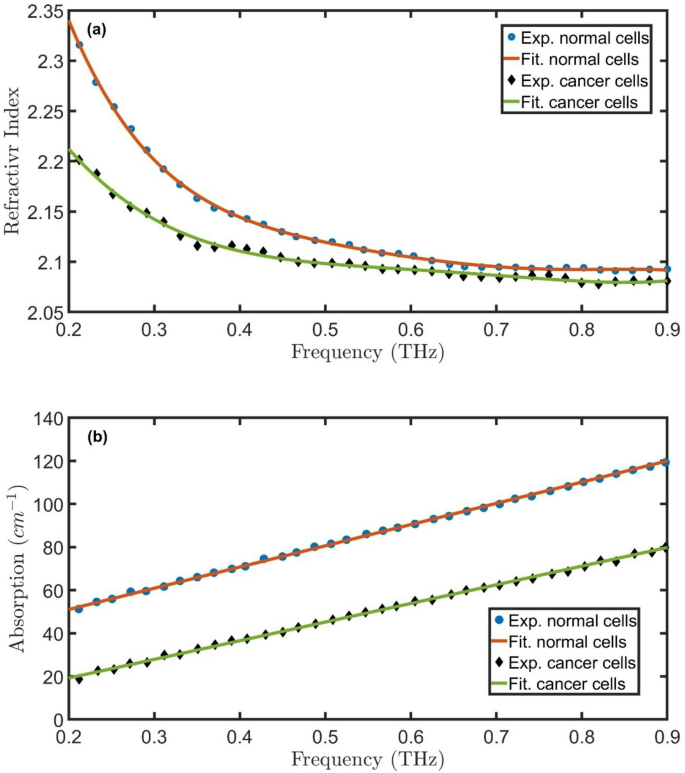
Figure 2(a-b) represent the absorption and real RI of normal and cancered oral samples at room temperatures. At room temperature, water absorption in the THz range becomes more pronounced, potentially obscuring subtle differences between tissue types. The frequency-dependent dispersion of the refractive index would still follow a decreasing trend with increasing frequency, but with broader peaks due to enhanced molecular relaxation processes. Despite these challenges, the persistent contrast in refractive index between normal and cancerous tissues suggests that THz imaging could remain viable for ex vivo diagnostics at room temperature. The RI and absorption of normal oral samples has higher values than the cancered cells.
Experimental25 and fitted (a) real RI and (b) absorption of normal and cancered oral samples at room temperatures.
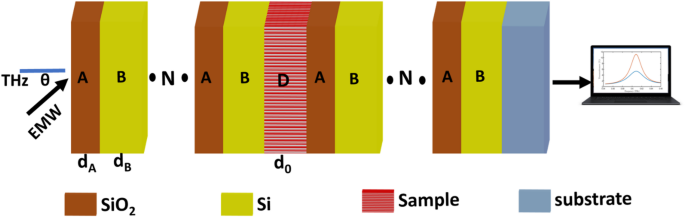
In the following, the transmittance of \(\:{\left(A*B\right)}^{N}{\left(A*B\right)}^{N}*substrate\) will be studied. The \(\:{n}_{A}\), \(\:{n}_{B}\), \(\:{d}_{A},\) and \(\:{d}_{B}\) are 2.1, 3.4, 65 \(\:\mu\:m\), and 35 \(\:\mu\:m\), respectively. Due to contrasting dielectric properties and periodic RI modulation between \(\:Si{O}_{2}\) and \(\:Si\), a PBG with central frequency of 0.58 THz, as clear in Fig. 3. \(\:Si\) has a high refractive index (~ 3.4 in the THz range), while \(\:Si{O}_{2}\) exhibits a lower index (~ 2.1), creating strong dielectric contrast. When arranged in a periodic lattice, this contrast leads to Bragg scattering, where certain THz frequencies are completely reflected due to destructive interference while others propagate. The PBG appears when the lattice periodicity matches the THz wavelength, preventing electromagnetic wave propagation in specific frequency ranges. The PBG’s position and width depend on the lattice geometry, filling ratio of \(\:\text{S}\text{i}/Si{O}_{2}\), and incident wave polarization. The PBG can be tuned by adjusting structural parameters. Additionally, the low THz absorption of \(\:Si{O}_{2}\) helps maintain sharp band edges, while silicon’s high index enhances light confinement, making \(\:\text{S}\text{i}/Si{O}_{2}\) PhCs efficient for THz filtering, sensing, and slow-light devices. The value of the central frequency of the PBG is compatible with the theoretical equation40:
$$\:{f}_{PBG}=\frac{{c}_{0}\:({n}_{A}+{n}_{B})}{4({d}_{A}+{d}_{B})\left({n}_{A}{n}_{B}\right)},$$
(13)
where \(\:{c}_{0}\) is the speed of light in vacuum.
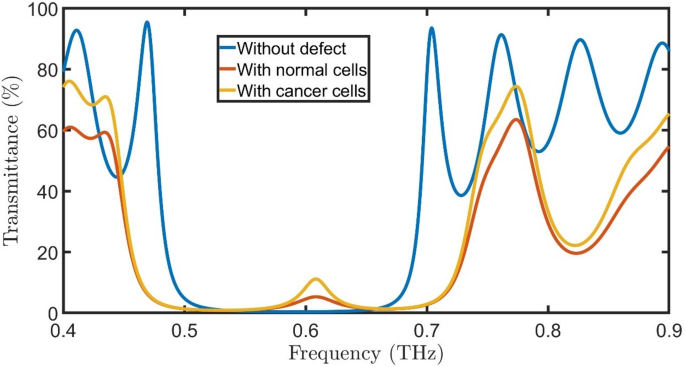
Transmittance of proposed oral cancer detector \(\:{\left(A*B\right)}^{N}\left(D\right){\left(A*B\right)}^{N}*substrate\) without defect, with normal cells, and with cancered cells at room temperature, \(\:N=4\), initial \(\:\theta\:\) of zerro degree, and \(\:{d}_{0}\) of 50 \(\:\mu\:m\).
When a defect composed of normal oral cells with a thickness of 50 \(\:\mu\:m\) is introduced into a \(\:\text{S}\text{i}/Si{O}_{2}\) PhC, a resonant peak of \(\:{f}_{R}=\)0.61 THz, T= 5.3%, and bandwidth (FWHM) of 0.037 THz emerges within the PBG due to localized mode confinement. The PBG normally prohibits electromagnetic wave propagation at specific THz frequencies; however, the defect disrupts the periodic dielectric structure, creating a localized state that allows certain frequencies to resonate. Normal oral cells have distinct dielectric properties (refractive index and absorption) compared to the surrounding PhC lattice, forming a cavity-like region where THz waves become trapped. This defect-induced cavity supports standing waves at a particular resonant frequency, leading to a transmission peak within the forbidden band gap.
The position and intensity of the resonant peak depend on the defect’s thickness, RI contrast, and geometric placement within the PhC. Since normal oral cells exhibit different THz optical properties than \(\:\text{S}\text{i}/Si{O}_{2}\), their integration modifies the local electromagnetic field distribution, enhancing light-matter interaction at the defect site. This principle is exploited in biosensing applications, where the resonant frequency change can indicate variations in cell composition or pathology. The defect-mediated resonance thus enables precise detection of tissue abnormalities, leveraging the high sensitivity of PhCs to minute dielectric changes. Replacing the normal oral cells with cancered cells changes the resonant peak to \(\:{f}_{R}=\)0.61 THz, \(\:T=\:11.1\:\%,\) and FWHM of 0.0268 THz. As the RI contrast between cancered and normal cells is very small, the peak position doesn’t change. The transmittance of cancered peak cells is higher than the normal cell’s peak because the absorption of normal cells is higher than that of cancered cells, as clear in Fig. 2b.
Geometry of \(\:{\left(A*B\right)}^{N}\left(D\right){\left(A*B\right)}^{N}*substrate\) as oral cancer detector according to PT symmetry.
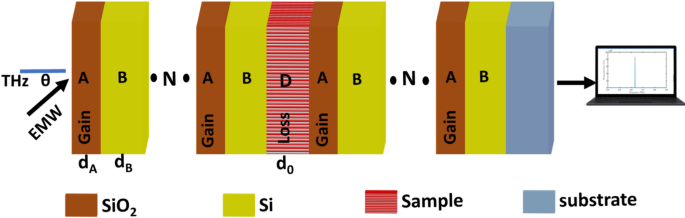
To enhance the \(\:T\) and FWHM of peaks, \(\:Si{O}_{2}\) layers will be doped with quantum dots to get gain layers in the first PhC and loss layers in the second PhC41,42, as clear in Fig. 4. The proposed photonic structure incorporates an optically pumped gain layer to enhance its performance characteristics. When externally pumped with an optical source, the quantum dots embedded within the gain layer absorb photons at specific resonant frequencies. Through the process of stimulated emission, these excited quantum dots subsequently re-emit photons at the same characteristic frequencies. This coherent emission process effectively amplifies the propagating electromagnetic waves within the structure, leading to significant enhancement of the optical signal.
The amplification mechanism relies fundamentally on the precise coupling between the system’s inherent resonant peaks and the frequencies re-emitted by the quantum dots. This interaction creates constructive interference that magnifies the signal intensity at the desired operational frequencies. The gain layer’s ability to compensate for optical losses while simultaneously amplifying the signal stems from its carefully engineered complex refractive index, expressed as \(\:{n}_{gain}={n}_{R}-i\:0.01\:Q\), where \(\:{n}_{R}\) represents the real component, and \(\:Q\) denotes the gain factor. This formulation allows for controlled light amplification within the photonic structure.
Complementing the gain layer, the loss layer features a corresponding refractive index profile given by \(\:{n}_{loss}={n}_{R}+i\:0.01\:Q\). The balanced opposition between these gain and loss components creates a stable system where the imaginary parts of the refractive indices (\(\:\pm\:0.01Q\)) precisely govern the amplification and attenuation characteristics. This parity between gain and loss mechanisms enables exceptional control over light propagation dynamics while maintaining system stability.
The strategic implementation of quantum dot gain media combined with refractive index engineering offers several operational advantages. The stimulated emission from quantum dots provides frequency-selective amplification that can be precisely tuned through optical pumping parameters. Meanwhile, the complex refractive index modulation allows for dynamic control over light-matter interactions within the structure. Together, these features enable the development of advanced photonic devices with enhanced signal processing capabilities, improved signal-to-noise ratios, and tunable spectral response characteristics, making this approach particularly valuable for applications requiring controlled optical amplification and manipulation.
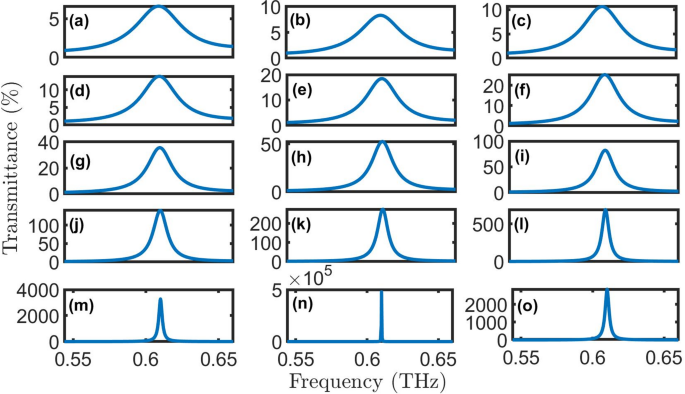
Transmittance of proposed oral cancer detector \(\:{\left(A*B\right)}^{N}\left(D\right){\left(A*B\right)}^{N}*substrate\) with normal cells at room temperature, N = 4, initial \(\:\theta\:\) of zerro degree, and \(\:{d}_{0}\) of 50 \(\:\mu\:m\) for (a) \(\:Q=1\), (b) \(\:Q=2\), (c) \(\:Q=3\), (d) \(\:Q=4\), (e) \(\:Q=5\), (f) \(\:Q=6\), (g) \(\:Q=7\), (h) \(\:Q=8\), (i) \(\:Q=9\), (j) \(\:Q=10\), (k) \(\:Q=11\), (l) \(\:Q=12\), (m) \(\:Q=13\), (n) \(\:Q=14\), and (o) \(\:Q=15\).
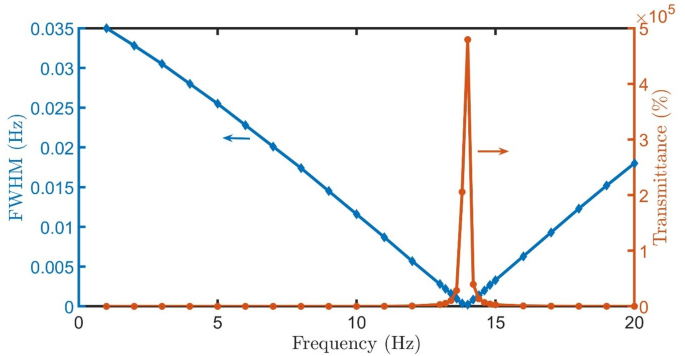
The transmittance spectra in Fig. 5(a-o) demonstrate the optical behavior of the proposed PhC structure \(\:{\left(A*B\right)}^{N}\left(D\right){\left(A*B\right)}^{N}*substrate\) under varying gain/loss conditions (\(\:Q\)). All simulations assumed normal incidence (\(\:\theta\:\:=\:0^\circ\:\)) at room temperature conditions. The spectra reveal a well-defined resonant peak centered near 0.61 THz that exhibits remarkable sensitivity to the loss parameter \(\:\kappa\:\). At low loss (\(\:\kappa\:\:=\:0.01-0.03,\:Q=1-3\)), the resonance appears broad with transmittance below 10%, indicating strong absorption. In moderate gain/loss conditions (\(\:\kappa\:\:=\:0.04-0.09,\) \(\:Q=4-9\)), the peak narrows significantly while achieving 40-100% transmittance, suggesting optimal balance between gain/loss factor and light localization. For higher gain/loss factor (\(\:\kappa\:\:=\:0.10-0.15,\:Q=10-15\)), the resonance becomes extremely sharp with transmittance amplification exceeding 2000%, demonstrating the structure’s ability to enhance specific frequencies despite increased absorption. The highest transmittance and lowest FWHM are achieved for healthy cells at \(\:Q=14\), as clear in Fig. 6.
FWHM and Transmittance of proposed detector \(\:{\left(A*B\right)}^{N}\left(D\right){\left(A*B\right)}^{N}*substrate\) with healthy cells versus Q at room temperature, \(\:N=4\), initial \(\:\theta\:\) of zerro degree, and \(\:{d}_{0}\) of 50 \(\:\mu\:m\).
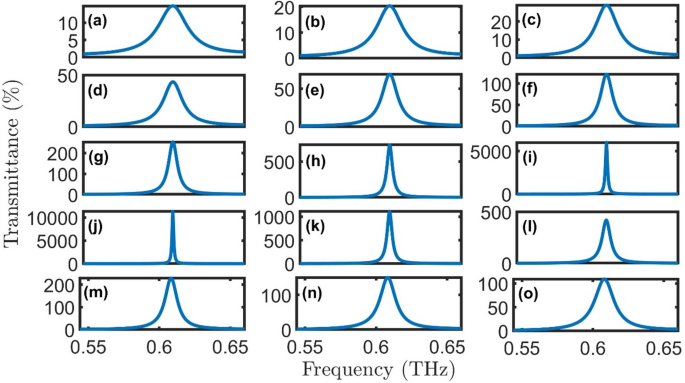
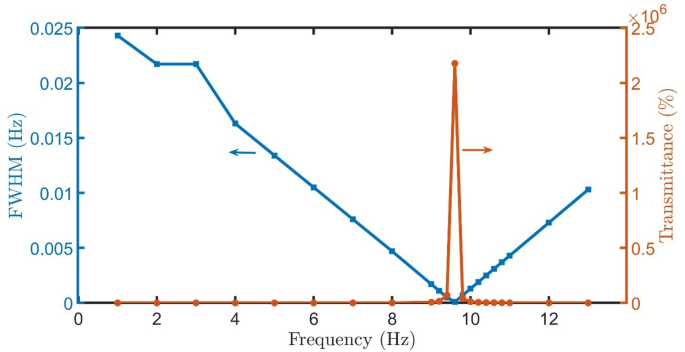
By replacing the healthy cells with oral cancer sample, the spectra reveal a well-defined resonant peak nearly at the same position (0.61 THz) and exhibits remarkable sensitivity to the gain/loss parameter κ, as clear in Fig. 7(a-o). At low gain/loss factor (\(\:\kappa\:\:=\:0.01-0.06,\:Q=1-5\)), the resonance appears broad with transmittance below 100%, indicating strong absorption. In moderate gain/loss conditions (\(\:\kappa\:\:=\:0.06-0.08,\:Q=6-8\)), the peak narrows significantly while achieving 100-600% transmittance. For gain/loss factor (\(\:\kappa\:\:=\:0.09-0.10,\:Q=9-10\)), the resonance becomes extremely sharp with transmittance amplification exceeding 5000%, demonstrating the structure’s ability to enhance specific frequencies despite increased absorption. The highest transmittance and lowest FWHM are achieved for healthy cells at \(\:Q=9.6\), as clear in Fig. 8.
Transmittance of proposed oral cancer detector \(\:{\left(A*B\right)}^{N}\left(D\right){\left(A*B\right)}^{N}*substrate\) with cancer cells at room temperature, \(\:N=4\), initial \(\:\theta\:\) of zerro degree, and \(\:{d}_{0}\) of 50 \(\:\mu\:m\) for (a) \(\:Q=1\), (b) \(\:Q=2\), (c) \(\:Q=3\), (d) \(\:Q=4\), (e) \(\:Q=5\), (f) \(\:Q=6\), (g) \(\:Q=7\), (h) \(\:Q=8\), (i) \(\:Q=9\), (j) \(\:Q=10\), (k) \(\:Q=11\), (l) \(\:Q=12\), (m) \(\:Q=13\), (n) \(\:Q=14\), and (o) \(\:Q=15\).
The extraordinary performance of our PhC biosensor stems from its carefully designed parity-time (PT) symmetric configuration. This non-Hermitian system achieves perfect balance between gain and loss regions, creating unique optical properties not found in conventional structures. The periodic arrangement of layers with properly tuned imaginary refractive index components (\(\:\kappa\:\:=\:0.01Q\)) establishes the necessary PT-symmetric condition. This balanced gain-loss distribution enables the system to operate near an exceptional point, where eigenvalues and eigenvectors coalesce, producing the ultra-sharp resonant peaks observed in our simulations.
The PT-symmetric design transforms optical loss into a performance-enhancing feature through several interconnected mechanisms. First, the system’s operation near an exceptional point creates extreme sensitivity to perturbations while maintaining stable resonance conditions. This explains why increasing the loss parameter (\(\:\kappa\:\)) actually improves the resonant peak quality – a counterintuitive result impossible in ordinary photonic structures. Second, the non-Hermitian nature of the system enables unusual energy localization effects, where the electric field becomes strongly enhanced precisely at the defect layer containing biological samples. This field enhancement directly boosts the sensor’s sensitivity to minute changes in cell properties.
FWHM and Transmittance of proposed detector \(\:{\left(A*B\right)}^{N}\left(D\right){\left(A*B\right)}^{N}*substrate\) with cancer cells versus \(\:Q\) at room temperature, \(\:N=4\), initial \(\:\theta\:\) of zerro degree, and \(\:{d}_{0}\) of 50 \(\:\mu\:m\).
For oral cancer detection, the PT-symmetric design offers three crucial benefits. The exceptional point physics provides: (1) orders-of-magnitude better sensitivity to small refractive index changes between healthy and cancerous cells (Fig. 9), (2) inherent noise rejection by suppressing all frequencies except the sharp resonance, and (3) stability against fabrication imperfections. As our results show, these advantages become particularly pronounced at higher \(\:Q\) values (\(\:Q=9-14\)), where the system operates in the optimal PT-broken phase. This creates the ideal conditions for medical diagnostics – extremely narrow resonances for precise detection combined with strong transmission for reliable signal acquisition.
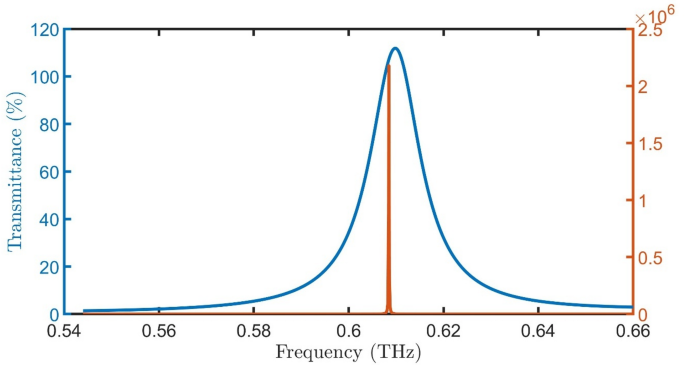
Transmittance of proposed oral cancer detector \(\:{\left(A*B\right)}^{N}\left(D\right){\left(A*B\right)}^{N}*substrate\) with oral healthy and cancer cells at room temperature, \(\:N=4\), initial \(\:\theta\:\) of zerro degree, \(\:{d}_{0}\) of 50 \(\:\mu\:m\), and \(\:Q=9.6\).
The proposed PT-symmetric PhC sensor demonstrates exceptional sensitivity to refractive index variations, as quantified by two complementary metrics. The spectral sensitivity \(\:S\left(f\right)=\frac{\varDelta\:{f}_{R}}{\varDelta\:{n}_{cells}}=118\:\text{G}\text{H}\text{z}/\text{R}\text{I}\text{U}\) characterizes the resonant peak shift per refractive index unit (RIU) change, indicating that minute variations in cellular dielectric properties produce measurable frequency displacements. This level of sensitivity enables detection of subtle biomolecular changes associated with early-stage oral cancer development.
The transmittance-based sensitivity \(\:S\left(T\right)=\frac{\varDelta\:T}{\varDelta\:{n}_{cells}}=1.9\times\:{10}^{8}\:\%/RIU\) reveals even more remarkable performance, representing an extraordinary amplification of optical response to refractive index perturbations. This exceptionally high value stems from the PT-symmetric design’s ability to convert small index variations into dramatic transmittance changes through its exceptional point-enhanced resonance. The dual-sensitivity mechanism provides robust detection capability – spectral shifts offer absolute measurements while transmittance changes provide amplified signals for low-concentration biomarkers.
These sensitivity values substantially surpass conventional photonic biosensors, particularly in the critical terahertz frequency range. The spectral sensitivity of 118 GHz/RIU represents a high improvement over typical PhC sensors, while the transmittance sensitivity of \(\:1.9\times\:{10}^{8}\:\%/RIU\) demonstrates unprecedented response amplification. This performance advantage originates from the PT-symmetric design’s unique ability to transform small refractive index perturbations into strongly amplified optical signals through its carefully balanced gain-loss configuration and exceptional point dynamics.
Table 1 Comparative analysis with existing sensor technologies.
Table 1 presents a systematic performance comparison between our proposed PT-symmetric PhC sensor and previously reported biosensing devices. Our sensor demonstrates significant improvements across all key metrics when benchmarked against conventional approaches. The spectral sensitivity of 118 GHz/RIU represents a 2-fold enhancement over the best-performing PhC biosensor reported in literature50. More remarkably, the transmittance sensitivity of \(\:1.9\times\:{10}^{8}\:\%/RIU\) surpasses existing optical sensors, establishing a new benchmark for label-free detection. In addition, the quality factor (\(\:Q-factor=\frac{{f}_{R}}{FWHM}\)) and limit of detection (\(\:LoD=\frac{{f}_{R}}{20\:S\:Q-factor}\)) recorded high performance.
The comparison reveals two distinct advantages of our PT-symmetric design: superior sensitivity-to-footprint ratio enabled by exceptional point physics, and inherent noise rejection capability through the PT-symmetric filtering mechanism. These performance metrics position our sensor as a potentially transformative technology for early cancer diagnosis, particularly where conventional methods struggle with limited sensitivity or require complex labeling procedures.
While this study primarily correlates detection signals with refractive index (RI) changes, we recognize that real-world biological samples (e.g., cells and tissues) exhibit additional complexities such as variations in morphology, density, and heterogeneous biomolecule composition. These factors collectively contribute to the local RI distribution and can imprint distinct signatures on the resonance spectrum (e.g., peak broadening, asymmetric shifts, or secondary modes). Critically, our platform’s high sensitivity to RI gradients inherently captures these composite effects, as they manifest in the measured optical response. For practical applications, calibration protocols using control samples or complementary techniques (e.g., machine learning-aided deconvolution) could disentangle these intertwined contributions. Future work will systematically quantify such multifactorial interactions to enhance the sensor’s specificity in complex media.
While the proposed theoretical design demonstrates promising performance, practical implementation requires consideration of fabrication challenges and tolerances. The sensor structure, composed of Si, SiO₂-doped layers, may encounter deviations in layer thicknesses or refractive indices during experimental manufacturing due to deposition control, etching precision, or material inhomogeneity. Such variations can shift the resonant peak position and alter the optimal Q parameter. However, the underlying physical mechanism remains intact, enabling post-fabrication optimization through recalibration.