Photonic information processing relies heavily on Gaussian building blocks, and researchers increasingly recognise that adaptive measurement and feedforward are crucial for achieving truly powerful computation, with the number of adaptive steps acting as a key measure of computational ability. Changhun Oh and Youngrong Lim, from the Department of Physics at Chungbuk National University, alongside their colleagues, now demonstrate a surprising distinction between this adaptive computation and traditional benchmarks of power. Their work reveals that estimating observable expectation values, a task fundamental to simulation, remains efficiently solvable by classical computers when adaptive measurements are limited, even with complex non-Gaussian inputs, whereas increasing the number of adaptive steps quickly pushes the problem beyond classical capabilities. This finding establishes a clear boundary between classical simulability and potential quantum advantage, offering a new perspective on the power of measurement-adaptive Gaussian circuits and introducing improved classical techniques for analysing these systems.
Rather than assessing power only through sampling problems, researchers are focusing on tasks with practical relevance, such as the quantum mean-value problem, which estimates observable expectation values crucial for simulation and variational algorithms. Their analysis of bosonic circuits with adaptivity demonstrates that even with substantial non-Gaussian resources, the mean-value problem can remain efficiently solvable for classical computers when the number of adaptive measurements is limited. Conversely, when fewer constraints are applied, the problem becomes computationally hard, revealing valuable insights into the limits of quantum advantage for this type of calculation.
Efficient Loop Hafnian Calculation for Low-Rank Matrices
This work details a method for efficiently calculating the loop hafnian of a matrix, particularly when the matrix has a low-rank structure. The loop hafnian, a generalization of the determinant important for areas like Gaussian processes and statistical mechanics, requires efficient calculation for many applications. The core idea is to exploit the low-rank structure to reduce computational complexity. If a matrix has a rank much smaller than its dimension, it can be decomposed into a simpler form. This decomposition, combined with a polynomial representation of the loop hafnian, allows the algorithm to rewrite the calculation as a sum of terms involving fewer calculations.
The algorithm proceeds by decomposing the matrix, expressing the loop hafnian as a polynomial, expanding the polynomial to identify coefficients, and then evaluating the polynomial to obtain the final result. Calculating the loop hafnian directly would typically require exponential time, but this low-rank algorithm reduces the complexity to polynomial time, with a complexity of O(n * |P2n,r|), where |P2n,r| represents the number of integer partitions. If the rank is fixed, the complexity becomes linear with the size of the matrix, making it crucial for calculating specific matrix elements. This work presents a sophisticated algorithm for efficiently calculating the loop hafnian of a low-rank matrix, reducing computational complexity from exponential to polynomial time.
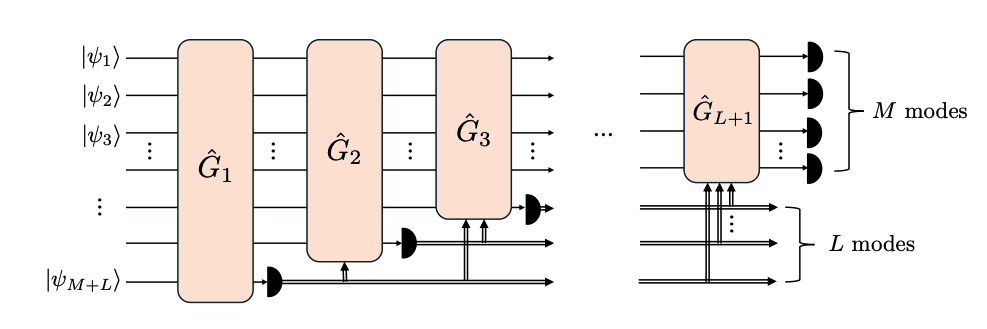
Adaptive Measurements Define Quantum Computational Advantage
Researchers have established a critical boundary between classical and quantum computational power when simulating photonic circuits. They demonstrate that the complexity of computation depends on the number of adaptive measurements used. While non-Gaussian resources typically make sampling problems intractable for classical computers, the quantum mean-value problem can remain efficiently solvable even with substantial non-Gaussian input, provided the number of adaptive measurements is limited. This contrasts with sampling, where even modest non-Gaussian elements often lead to computational hardness.
The research demonstrates that classical algorithms can efficiently estimate expectation values for product observables when the number of adaptive measurements is constant and the observable’s operator norm is polynomially bounded. Detailed analysis of three circuit families, Gaussian circuits without feedforward, those with photon-number-resolving detection, and those utilizing Gaussian measurements, reveals a clear progression towards universal quantum computation. Circuits incorporating sufficient photon-number or Gaussian measurements for feedforward achieve universality, at which point the quantum mean-value problem becomes BQP-complete. This work clarifies the transition from classically easy circuits to those capable of universal quantum computation, establishing a crucial link between the number of measurements and computational complexity.
Efficient Classical Simulation of Gaussian Circuits
This work presents classical algorithms for solving the quantum mean-value problem within Gaussian circuits, and also for circuits incorporating photon-number-resolving measurements with Gaussian feedforward, or Gaussian measurements with Gaussian feedforward. These findings demonstrate that, unlike sampling problems where non-Gaussian resources often create classical hardness, mean-value estimation can remain classically tractable if the number of adaptive measurements is limited. The study highlights the importance of low-mode and low-rank structures in enabling efficient classical simulation of certain bosonic computations, and clarifies the boundaries between classical and quantum complexity in these systems. While the generalized algorithm performs efficiently when the number of measurements is constant, improving the practical running time remains an open question. Further research will explore whether the algorithm can be made efficient even when the number of measurements scales logarithmically with system size, aiding future studies of bosonic circuits as benchmarks for quantum experiments.