Our choice of epitaxial V(100)/MgO/Fe(100) junctions appears surprising. The incompatible orbital symmetries in the electronic structure of V(100) and Fe(100), suggest that their junctions are nonconducting in the low-bias regime33,34,35. Early experiments on heteroepitaxial superconducting Fe/V/Fe junctions reveal the importance of the relevant orbital symmetries and how they can determine desirable spin-dependent transport properties36.
At the Fermi level EF, Δ2 orbital symmetry of V is absent for Fe, which is characterized by Δ1 symmetry, shown in Fig. 1a. Since MgO is an insulator filtering out Δ2 and producing giant tunneling magnetoresistance (TMR) in Fe/MgO/Fe junctions33,34,35,37,38, proximity-induced superconductivity from V across MgO into Fe seems even less likely. However, structural inversion asymmetry in our junctions leads to interfacial SOC, which accompanies the effective Δ2 barrier in crystalline MgO due to its filtering effect. The SOC-induced spin-flip scattering mixes Δ2 and Δ1 symmetries and creates a mechanism for electron tunneling above TC across the junction at low bias, shown in Fig. 1a. Our first-principles calculations (see Supplementary Information, Section I, SI-I) also confirm the presence of Rashba SOC at the V/MgO interfaces. Another low-bias contribution in these epitaxial junctions with conserved wave vector parallel to the interfaces, k||, comes from “hot spots” for normal incidence at k|| = 0 (the Γ point), which provides high transmission through MgO33. A simple picture for the normal-state transport in this junction is described by an equivalent resistance, Req = RSOC + RMgO, in which the resistance of the symmetry-related SOC barrier, RSOC, is much larger than the resistance from the conventional barrier strength of the MgO region, RMgO.
Fig. 1: Orbital symmetry change and normal-state transport in epitaxial V/MgO/Fe-based junctions.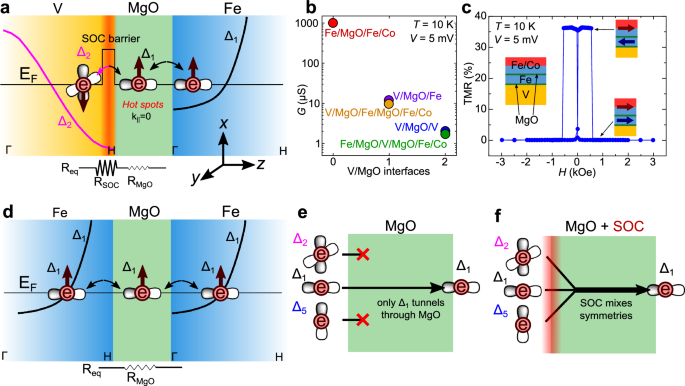
a The main conductance bands, labeled with their respective orbital symmetries, are superimposed to each region. Arrows denote electron spin. At the Fermi level, EF, in vanadium, only electrons with Δ2 symmetry are present, while they are absent in iron. Therefore, a symmetry change is necessary for the electron transport across the V/MgO/Fe junction. This is enabled by the Rashba spin-orbit coupling (SOC) at the V/MgO interface. MgO acts both as (i) symmetry filter at EF, relatively transparent for Δ1 electrons in iron at the normal incidence (vanishing wave vector along the interface, k|| = 0), while having a strong barrier for Δ2 electrons and (ii) enabling the symmetry and spin changes allowing electron tunneling into the iron. An equivalent resistor model indicates that the SOC barrier dominates over the usual barrier from the MgO region. b Typical normal-state conductance of different tunnel junctions of a lateral size 20 × 20 μm2, as a function of their number of V/MgO barriers. Each dot: sample-averaged conductance. Each extra V/MgO barrier diminishes the conductance by an order of magnitude. c In-plane tunnel magnetoresistance (TMR) of a spin-valve junction (inset), showing parallel and antiparallel magnetization configurations, changing with an applied magnetic field, H, and the typical coercive field of the hard Fe/Co magnetic layer. d Across the less-resistive Fe/MgO/Fe junction, the transport is dominated by Δ1 electrons without SOC barrier. e, f The absence (presence) of SOC removes (enables) orbital symmetry mixing, explaining the measured relative magnitudes of conductance in (b).
This picture of the tunneling dominated by symmetry-enforced spin filtering, rather than by the barrier strength, is confirmed by the measured low-bias differential conductance G shown in Fig. 1b, revealing the key role of SOC at the V/MgO interface. Compared to junctions without such an interface, G is reduced by two (three) orders of magnitude with one (two) interface(s). For in-plane magnetization in a V/MgO/Fe/MgO/Fe/Co junction, shown in Fig. 1c, the obtained TMR = (GP – GAP)/GAP~40%, where GP (GAP) corresponds to parallel (antiparallel) magnetization in the two Fe regions, signals highly spin-polarized electrons. By excluding the nonmagnetic V/MgO region, we have shown an even higher TMR~330% in Fe/MgO/Fe/Co junctions38. Using shot noise measurements, we can also exclude the role of pinholes in determining G (details of sample fabrication, measurements, and characterization can be found in Methods, SI-II and Ref. 31). To further support our conductance measurements across different junctions, it is helpful to consider a schematic illustration of the role of dominant orbital symmetries and their SOC-induced mixing in Fig. 1d–f. The highest measured conductance in Fig. 1b is found for the Fe/MgO/Fe-based junction in which the dominant Δ1 symmetry is shared by all the regions and the related transport does not experience the symmetry mismatch (no SOC barrier). However, for junctions with regions characterized by other orbital symmetries, the spin-filtering exclusion from the MgO can be overcome by SOC mixing and accompanied by a large RSOC, consistent with the results in Fig. 1b.
In the superconducting state, as shown in Fig. 2a, transport is distinguished by Andreev reflection, providing the microscopic mechanism for proximity-induced superconductivity13,17. In conventional Andreev reflection, an electron is reflected backwards and converted into a hole of opposite charge and spin. With no interfacial barrier, this implies the doubling of the normal-state GN: two electrons are transferred across the interface into S, where they form a spin-singlet Cooper pair39. Because of spin polarization P in F, not all electrons can find a partner of opposite spin to undergo Andreev reflection17,40. Together with the normal (ordinary) reflection at the interfacial barrier, such a finite P suppresses the Andreev reflection and reduces G40 at applied bias V<Δ/e below the effective superconducting gap Δ ~1.05 meV, where -e is the electron charge. A small peak in G(V\( \sim \)Δ/e) and a substantial value of G(V = 0) (Fig. 2a) suggest that S/F is not a typical tunnel junction and has only a moderate interfacial barrier strength. The inset in Fig. 2a indicates TC ~ 4 K, as identified by the measured temperature-dependent conductance.
Fig. 2: Bias dependence of the conductance and giant shot noise in a V/MgO/Fe junction.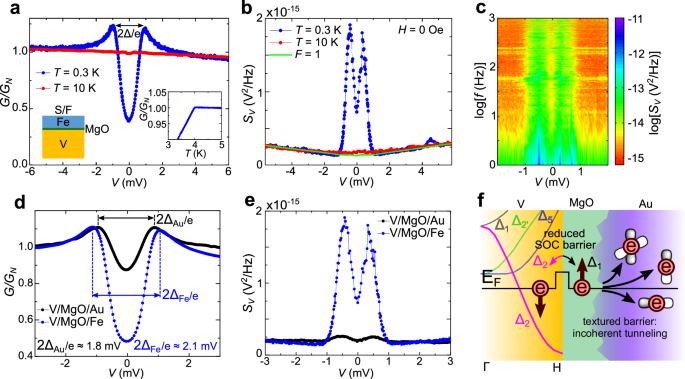
a Conductance for a superconductor/ferromagnet (S/F) sample (sketched in the left), above (red) and below (blue) the critical temperature of vanadium, TC, normalized by the conductance at bias V = −5 mV, above the effective superconducting gap, Δ, -e is the electron charge. Inset: TC identified by the measured temperature-dependent subgap conductance. b For the same sample, there is giant shot noise below TC (blue) at low bias, eV < Δ, compared to its value above TC (red), and its corresponding theoretical maximum value given by the Fano factor, F = 1 (green), for the normal state. c The evolution of the shot noise power with frequency, f, and V, shown in the logarithmic scale. The noise spectrum is largely f independent, except near the lowest f. d, e Comparison of the bias-dependent conductance and shot noise with the control V/MgO/Au junction, with the same normalization as in (a). f Schematic role of the MgO/Au nonepitaxial growth leading to the highly textured interface and suppressed filtering due to different orbital symmetries.
A high-quality MgO barrier defines the location of the voltage drop and thus enables accurate shot noise measurements, previously absent in S/F junctions. Unlike the measured G(V), similar to what was observed in various superconducting structures, the shot noise in Fig. 2b for the same S/F junction shows an unprecedented giant low-bias increase at T = 0.3 K < TC, orders of magnitude larger than theoretically expected. With fluctuations due to the discreteness of the electrical charge, it is common to introduce the current shot noise power SI,max = 2q < I> transferred in discrete units of charge q, where <I> is the average current10,11,41,42. To describe the ratio between the shot noise and the conductance, it is useful to introduce the Fano factor10,11 F = SI/(2eG | V | ). This Fano factor also gives the effective charge responsible for the shot noise10,11. For a fully random (Poisson) process of uncorrelated electrons, SPoisson = 2e<I > , F in the normal state attains at maximum F = 1, while F = 2 for superconducting tunnel junctions11 signals that |q | = 2e since the shot noise originates from the transfer of Cooper pairs. With a finite circuit resistance, our measurements also include voltage fluctuations with the resulting voltage shot noise power10,42,43 SV = F2e < I > /G2 (SI-II provides the expression for T > 0), shown together with the expected maximum normal-state value for F = 1. Remarkably, at T = 0.3 K and eV < Δ, we can infer F > 100, as if a giant effective charge |q | > 100 e is responsible for the observed shot noise! This striking behavior is the hallmark of the superconducting state, while at eV > Δ or T > TC, SV approaches the Poisson value for F = 1 (green line). Another distinguishing feature of the giant SV in the superconducting state is its independence of frequency f, shown in Fig. 2c over two orders of magnitude in the frequency range. In contrast, the contribution of vortices43 is reflected in the 1/f-dependent part of the noise, decreasing with f and increasing with T, when T approaches TC (SI-III).
It is helpful to compare our prior conductance and shot noise results for S/I/F (V/MgO/Fe) junction with the measurements on a control S/I/N junction (V/MgO/Au). As expected, in Fig. 2d we find that the low-bias conductance is suppressed less in V/MgO/Au than that in V/MgO/Fe junction, consistent with the nonmagnetic Au and P = 0, as the Andreev reflection does not experience a large suppression from P = 0.7 at the Fe/MgO interface. Both junctions are not in a typical tunneling regime and they share only a small peak in G, known to appear at V\( \sim \)Δ/e. However, the separation of the two peaks is larger in V/MgO/Fe where, considering the commonly expected competition between ferromagnetism and superconductivity17,21, such a separation and the related superconducting gap should be reduced compared to the one in nonmagnetic V/MgO/Au. Since in both junctions we see that the superconducting gap exceeds the values expected for V itself, a larger peak separation in V/MgO/Fe would be consistent with a slightly larger proximity-induced gap than in V/MgO/Au (see discussion below). While the changes in the two corresponding gaps are moderate, turning to the comparison of the shot noise in Fig. 2e, we see a drastic increase in the measured low-bias shot noise of the V/MgO/Fe junction. These trends in the conductance and shot noise by replacing F by N region can be partially understood by recognizing the importance of the epitaxial growth and high-quality interfaces in V/MgO/Fe, while V/MgO/Au is an example of non-epitaxial growth leading to a highly textured interface and suppressed filtering due to different orbital symmetries, as depicted in Fig. 2f and SI-II. That the apparent superconducting gap is not more suppressed in V/MgO/Fe could signal the presence of spin-triplet superconductivity coexisting with ferromagnetism17,31.
The correlations among electrons, due to Coulomb repulsion and the Pauli exclusion principle, reduce the shot noise below its Poisson limit F = 1 (F = 2) in the normal (superconducting) state10,11. For example, in the fractional quantum Hall effect, the measured F = 1/3 signals the characteristic fractional charge4. Rare exceptions where the shot noise is enhanced compared to the Poisson value14,15,16 are typically observed in junctions with multiple superconducting regions without ferromagnets. To examine such excess shot noise, we consider a V/MgO/Fe/MgO/Fe/Co junction, used also to measure TMR in Fig. 1c. With the two different F regions, we can control the orientation of the Fe magnetization while the higher-coercivity Fe/Co magnetization remains fixed and serves as a sensor of the Fe magnetization through the measured TMR signal.
For the V/MgO/Fe/MgO/Fe/Co junction in Fig. 3a we see another example of a giant increase in the subgap shot noise, strongly suppressed by the out-of-plane (OOP) applied magnetic field, HOOP. This is further examined in Fig. 3b, which shows the suppression of the maximum value of the subgap shot noise with both HOOP and in-plane (IP) HIP. A stronger SV suppression with HOOP than with HIP is expected, just as for the OOP H-suppression of Δ (in the inset). However, the in-plane anisotropy (between [100] and [110] orientations for both SV and Δ) is surprising for conventional spin-singlet superconductivity and could instead signal an induced spin-triplet superconductivity. We also observe a slight increase in the noise with HIP, which can be attributed to the field-suppression of inherent magnetic textures. Similar trends in the suppression with V and H are also reproduced in the measured Fano factor in Fig. 3c, which reaches nearly F = 200.
Fig. 3: Anisotropic suppression of the giant shot noise by an applied magnetic field and bias.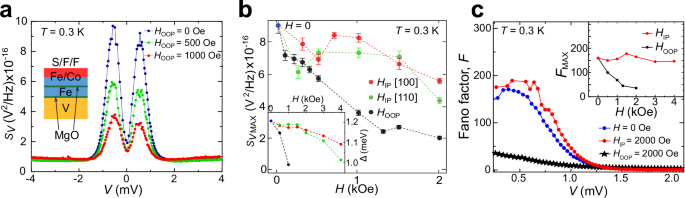
The measured spin-valve junction V/MgO/Fe/MgO/Fe/Co is the same as in Fig. 1c. a Out-of-plane (OOP) magnetic field effectively suppress the superconductivity and the observed low-bias shot noise. b Magnetic-field dependence of the maximum noise shot shows anisotropy, not only between in-plane (IP) and OOP (black), but also for IP easy (red) and hard (green) axis, which is unexpected for a spin-singlet superconductivity. Inset: anisotropic suppression of Δ for the same directions of applied magnetic field, H (same legend). c Evolution of the Fano factor, F, with applied bias and magnetic fields. The inset: the maximum Fano factor, FMAX, shown for a wide range of IP (red) and OOP (black) applied fields.
To seek a possible explanation of this peculiar behavior, we recall that normal-state transport in V/MgO/Fe-based junctions and our first-principles calculations confirm the presence of the interfacial SOC. Given the measured HIP noise anisotropy, such SOC influences the superconducting state and leads to spin-flip Andreev reflection with equal spin for electrons and holes, which is responsible for spin-triplet Cooper pairs17,44,45. As a result, SOC can partially counteract the suppression of Andreev reflection due to the high spin polarization, P \( \sim \) 0.7–0.8, of the Fe/MgO contact31, and the normalized interfacial barrier strength Z, such that the resulting low-bias G is higher than without SOC45. This is consistent with the data from Fig. 2a, which indicate only a moderate Z \( \sim \,\)1 (Z = 0 for perfect transparency and Z ≫ 1 for a tunnel junction). However, when we theoretically explore the shot noise in S/F junctions over a large parameter space for normalized barrier and Rashba SOC strength Z and λ (see Methods and SI-IVA, B), respectively, the maximum value is F = 2 (SI-IVC), orders of magnitude smaller than in Figs. 2b or 3c. With our analysis of the calculated shot noise in an effective 1D system, in the absence of spin polarization, it is possible to analytically express different scattering coefficients for the S/N junction and use them to evaluate the enhanced Fano factor for S/N/S Josephson junctions (SI-IVD).
The interplay of ferromagnetism and SOC is expected to generate proximity-induced spin-triplet superconductivity, but that alone cannot explain a huge excess of shot noise. Instead, prior examples of large shot noise14,15,16 suggest a resonant behavior which could naturally occur in Josephson junctions, with two superconducting regions and the formation of Andreev bound states, defined by multiple Andreev reflections (MAR)20,46. In the simple case of two identical superconducting gaps and Z = 0, one expects n = Δ/eV Andreev reflections, as if the charge transfer and the underlying shot noise could be described by a composite object with effective charge |q | = ne47. Support that only a single S region in nonmagnetic junctions could display properties of proximity-induced Josephson effect32,47,48 motivates us to revisit the understanding of S/F junctions. Proximity-induced spin-singlet superconductivity is strongly suppressed in F, such as Fe. However, its SOC-induced spin-triplet counterpart could coexist with ferromagnets, and we also consider that it is accompanied by an effective superconducting gap ΔF, and therefore supports MAR and enhances F beyond 2. The equal-spin superconducting correlations derived from the superconducting condensate inside V evolve dynamically through the interplay between SOC, symmetry-dependent tunneling, and the exchange interaction. The resulting phase evolution effectively decouples the proximity-induced superconducting correlations from the parent superconductor and supports MAR, which is also observed from preformed pairs6,7. This is unlike the usual proximity effects in S/F (S/N) junctions, where the proximitized order parameter is directly phase locked to that of S21.
A sketch of the physical mechanism for the giant shot noise and induced ΔF is depicted in Fig. 4a. The considered multiple electron-hole reflections are consistent with the abundance of these quasiparticles with Δ1 symmetry at the Fermi level of Fe(001), which easily tunnel through the MgO due to hot spots in momentum space. Multiple states with complex wave vectors in the MgO lead to interference effects in G31. The Fano factor gives the effective charge transfer through MAR across the apparent proximity-induced Josephson junction, formed by the vanadium s-wave superconductor and the resulting spin-triplet correlations in Fe. With this picture, we generalize the MAR15 calculation for G and the Fano factor to include the influence of SOC and normal reflections.
Fig. 4: Physical mechanism with calculated conductance and shot noise.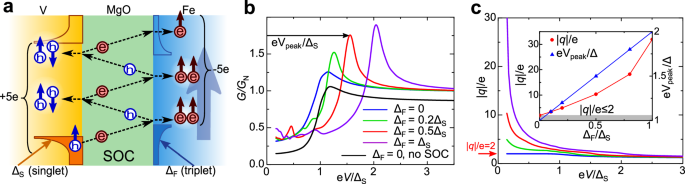
a Proximity-induced superconducting spin-triplet gap in Fe layer (blue), ΔF, and the interfacial spin-orbit coupling (SOC) support multiple spin-flip Andreev reflections in the V/MgO/Fe junction, which give rise to the excess charge transport (5e in the sketch) and the resulting low-bias excess Fano factor, h denotes holes. b Bias-dependent conductance without (black) and with SOC (colored lines) for different relative magnitudes of the induced spin-triplet gap, ΔF, and the spin-singlet gap, ΔS, in vanadium. Without SOC, there is a reduced junction transparency and conductance for all V. For comparison with experimental measurements, each curve with SOC is normalized by its conductance value well above the superconducting gap. The barrier and SOC strengths are parameterized by Z = 1 and λ= 1.2 (see Methods). c Calculated Fano factor or, equivalently, the effective charge ratio |q | /e, as a function of applied bias for the same parameters and a color code as given in (b). Inset: The corresponding evolution of the effective charge ratio (at eV/Δs = 0.1) and the conductance peak position with relative increase in ΔF. The gray area denotes the commonly expected Fano factor limited by 2.
This simple phenomenological model, nevertheless, captures several important experimental observations. With the calculated G in Fig. 4b we see that SOC enhances the interfacial transparency, consistent with the measurements from Fig. 2a which indicate only a moderate Z \( \sim \) 1, rather than the conventional tunnel junction with Z ≫ 1. By explicitly including ΔF > 0, we find that MAR-modified G no longer has the usual peak at the pure superconducting gap for vanadium, ΔS, but is shifted to higher values, eVpeak = ΔS + ΔF. Considering the broadening effect on the G–V curve due to thermal smearing and inelastic scattering in experiments, this peak position could be further shifted to higher energies49,50,51, leading to superconducting gaps (ΔFe, ΔAu) in Fig. 2d that exceed the expected BCS value of ΔS = 0.7 meV for vanadium with a measured critical temperature of TC ~ 4 K. Assuming that the spin-triplet gap is negligible in the S/I/N (V/MgO/Au) control junction and, based on the measured gaps (ΔFe, ΔAu) in Fig. 2d, we find ΔFe / ΔAu = (ΔF + ΔS) / ΔS ≈ 1.2, from which we estimate the induced gap ΔF ≈ 20% ΔS. With these parameters, we achieve an excellent fit to the experimental conductance (Fig. 2a, SI-IVF). This peak shift effect provides additional evidence for the proximity-induced triplet gap and the Josephson junction-like behavior in the S/I/F (V/MgO/Fe) junction.
Considering next the Fano factor, which in Fig. 4c is represented by |q |, the calculated effective charge transfer (SI-IVE), we confirm the essential role of proximity-induced ΔF, while a two-fold change of Z has only a very small influence. A finite ΔF, through MAR, allows for a large number of electron pairs to be transferred into the superconducting lead, resulting in a giant F near vanishing V. In the opposite large-bias limit, eV > ∆, |q| approaches the uncorrelated limit e, as the current is carried by independent quasiparticles. However, with ΔF = 0, the higher-order Andreev reflections alternate between the electron and hole pairs transferred into the superconducting lead, without any giant Fano factor. Even at vanishing V, the calculated |q| retains its conventional value of 2, known for S/N junctions10. The inset of Fig. 4c shows that the magnitude of the low-bias Fano factor grows with the increasing proximity-induced ΔF, together with an increased bias value for the peak position in G. Even in the extreme limit of ΔF = ΔS, our calculated results underestimate the measured Fano factor. We attribute this limitation to our simple and transparent description, which neglects the random scattering from the SOC barrier and the destructive interference52 suppressing the current (and therefore increasing F). Including these omitted effects could provide closer agreement with the measured Fano factor. Nevertheless, our theoretical framework already addresses the observed major puzzle. We provide a mechanism to exceed the expected theoretical limit F = 2 (shown in gray) with a single S region, while using the same parameters that describe the measured G(V) from Fig. 2a.
The significance of SOC and orbital symmetry selection in high-quality epitaxial junctions is further verified from our control V/MgO/V measurements (SI-II). One may expect that this conventional S/I/S Josephson junction would support an even larger Fano factor than in S/I/F junctions that we have studied. Indeed, experiments in NbN/MgO/NbN junctions confirm MAR and an enhanced shot noise15. Instead, with different orbital symmetries in V/MgO/V junctions, Δ2 in vanadium and Δ1 in MgO, both the conductance and subgap shot noise are suppressed several orders of magnitude as compared to V/MgO/Fe junctions.
These results suggest several important future opportunities. The proximity-induced Josephson effect in N/I/S junctions47,48 was observed through I-V curves or a zero-bias conductance peak (ZBCP), reproducing properties of conventional S/I/S Josephson junctions. Since the origin of similar ZBCP observations53 continues to be studied and attributed to resonant effects54,55,56, even without the proximity-induced second superconducting region, our noise spectroscopy could distinguish various scenarios and detect the proximity-induced Josephson effect. Our focus on a simple and transparent theoretical approach invites future theoretical extensions. Resonant effects alone would not support MAR and preclude our observed giant shot noise. Another ZBCP implication is its signature of Majorana states55 in spin-triplet topological superconductivity considered for fault-tolerant quantum computing17,22. However, an extrinsic ZBCP origin remains debated22,57, and shot noise spectroscopy could help to identify Majorana states58.
While Fe/MgO-based junctions have been extensively studied34,35, from commercial applications59 to integrating spintronics, electronics, and photonics60, there is only a limited understanding of their all-epitaxial growth with superconductors17,31. Since we show that even in the normal state for these junctions, their resistance is dominated by the symmetry-related SOC barrier (recall Fig. 1b), rather than the conventional barrier associated with the MgO regions, this motivates further studies to explore the superconducting spintronics in all-epitaxial superconductor junctions with ferromagnets, where the spin-triplet proximity and spin currents could be controlled by SOC. The role of SOC in proximity-induced spin-triplet topological superconductivity is well studied using semiconductor nanostructures17,22, but often overlooked in ferromagnetic junctions21,28,29,30. Shot noise spectroscopy could overcome these uncertainties, elucidating the role of SOC in systems where there remains a debate about the induced long-range spin-triplet superconductivity30,61,62. Our findings also pertain to materials design and emergent phenomena through various proximity effects, where buried interfaces play a crucial role13. While probing such interfacial properties poses a challenge for many scanning probes, our work demonstrates that even buried interfaces are directly accessible to noise spectroscopy.
