Odd-parity quasiparticle interference in the superconductive surface state of UTe2

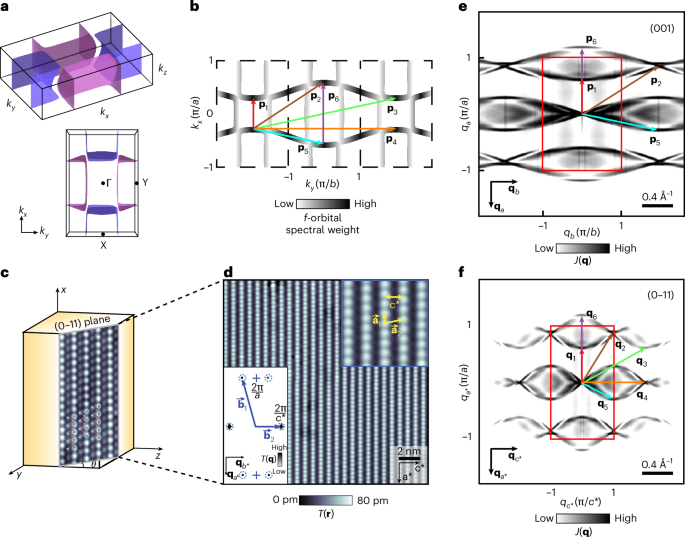
UTe2 normal-state electronic structure model

In this section, we first consider a four-band tight-binding model reproducing the quasirectangular FS of UTe2 and its undulations along \({k}_{z}\) axis, as outlined in ref. 48. The characteristic features are assumed to arise from the hybridization between two quasi-one-dimensional chains: one originating from the Te(2) 5p orbitals and the other from the U 6d orbitals. The lattice constants are taken to be \(a=0.41\) nm, \(b=0.61\) nm and \(c=1.39\) nm.

The coupling between the two Uranium orbitals is modelled by the following Hamiltonian:

$$\begin{array}{l}{H}_{{\rm{U}}-{\rm{U}}}=\\\left[\begin{matrix}{\mu }_{\rm{U}}-{2t}_{\rm{U}}\cos {k}_{x}a-{2t}_{{\rm{ch}},\rm{U}}\cos {k}_{y}b &-{\Delta}_{\rm{U}}-2{t}_{\rm{U}}^{{\prime} }\cos {k}_{x}a-2{t}^{\prime}_{{\rm{ch}},\rm{U}}\cos {k}_{y}b-4{t}_{z,\rm{U}}{e}^{-i{k}_{z}c/2}\cos {k}_{x}\frac{a}{2}\cos {k}_{y}\frac{b}{2}\\ -{\Delta}_{\rm{U}}-2{t}_{U}^{{\prime} }\cos {k}_{x}a-2{t}^{\prime}_{{\rm{ch}},\rm{U}}\cos {k}_{y}b -4{t}_{z,\rm{U}}{e}^{i{k}_{z}c/2}\cos {k}_{x}\frac{a}{2}\cos {k}_{y}\frac{b}{2} & {\mu }_{\rm{U}}-{2t}_{\rm{U}}\cos {k}_{x}a-{2t}_{{\rm{ch}},\rm{U}}\cos {k}_{y}b\end{matrix}\right]\end{array}$$

(6)

Here the tight-binding parameters are the chemical potential \({\mu }_{U}\), the intradimer overlap \({\Delta}_{U}\) of the uranium dimers (where two uranium atoms are coupled along the c axis and the dimers run along the a axis), the hopping \({2t}_{U}\) along the uranium chain in the a direction, the hopping \({t}_{U}^{{\prime} }\) to other uranium in the dimer along the chain direction, the hoppings tch,U and t′ch,U between chains in the a–b plane and the hopping tz,U between chains along the c axis.

Similarly, the coupling between the two tellurium orbitals is given by

$$\begin{array}{l}{H}_{{\rm{Te}}-{\rm{Te}}}=\\\left[\begin{matrix}{\mu }_{{\rm{Te}}}-{2t}_{{\rm{ch}},{\rm{Te}}}\cos {k}_{x}a &-{\Delta}_{{\rm{Te}}}-{t}_{{\rm{Te}}}{e}^{-i{k}_{y}b}-2{t}_{z,{\rm{Te}}}\cos {k}_{z}\frac{c}{2}\cos {k}_{x}\frac{a}{2}\cos {k}_{y}\frac{b}{2}\\-{\Delta}_{{\rm{Te}}}-{t}_{{\rm{Te}}}{e}^{i{k}_{y}b}-2{t}_{z,{\rm{Te}}}\cos {k}_{z}\frac{c}{2}\cos {k}_{x}\frac{a}{2}\cos {k}_{y}\frac{b}{2}&{\mu }_{{\rm{Te}}}-{2t}_{{\rm{ch}},{\rm{Te}}}\cos {k}_{x}a\end{matrix}\right]\end{array}$$

(7)

where the Te tight-binding parameters are the chemical potential μTe, the intra-unit-cell overlap ∆Te between the two Te(2) atoms along the chain direction, the hopping tTe along the Te(2) chain in the b direction, the hopping tch,Te between chains in the a direction and the hopping tz,Te between chains along the c axis.

The hybridization between the uranium and tellurium orbitals is given by

$${H}_{\rm{U}-{\rm{Te}}}=\left(\begin{array}{cc}\delta & 0\\ 0 & \delta \end{array}\right)$$

(8)

The normal-state tight-binding Hamiltonian of UTe2 can thus be written as

$${H}_{{\rm{UTe}}_{2}}=\left(\begin{array}{cc}{H}_{\rm{U}-\rm{U}} & {H}_{\rm{U}-{\rm{Te}}}\\ {H}_{\rm{U}-{\rm{Te}}}^{+} & {H}_{{\rm{Te}}-{\rm{Te}}}\end{array}\right)$$

(9)

We consider the following values for the tight-binding parameters (all parameter values are expressed in units of eV): \({\mu }_{\rm{U}}=-0.355,{\Delta}_{\rm{U}}\)\(=0.38,{t}_{\rm{U}}=0.17,\)\({t}_{\rm{U}}^{{\prime}}=0.08,{t}_{{\rm{ch}},\rm{U}}\)\(=0.015,{t}_{{\rm{ch}},\rm{U}}^{{\prime} }=0.01,\)\({t}_{z,\rm{U}}\)\(=-0.0375,{\mu}_{{\rm{Te}}}=-2.25,\)\({\Delta}_{{\rm{Te}}}\)\(=-1.4,{t}_{{\rm{Te}}}=-1.5,0,\)\({t}_{{\rm{ch}},{Te}}=0,{t}_{z,{\rm{Te}}}\)\(=-0.05,\delta =0.13\). These parameters are chosen to be consistent with both quantum oscillation measurements and our QPI data. All the hopping terms considered here are between the two nearest neighbours such that all scattering will be constrained to nearest neighbour sites at the surface. Any impurity potential is taken to be fully diagonal in the orbital basis with equal intensity on U orbitals and Te orbitals. These parameters are used in all simulations presented herein.

UTe2 superconductive energy-gap nodes and their (0–11) projections

Nodal locations presented in the main text are derived from the general expression for the electronic dispersion of a spin-triplet superconductor6

$${E}_{{\bf{k}}}^{\pm }=\sqrt{{\varepsilon }^{2}\left({\bf{k}}\right)+{|{\bf{d}}\left({\bf{k}}\right)|}^{2}\pm |{\bf{d}}({\bf{k}})\times {{\bf{d}}}^{* }({\bf{k}})|}$$

(10)

where \(\varepsilon \left({\bf{k}}\right)\) is the normal-state dispersion measured from the chemical potential and d(k) is the d-vector order parameter. The gap functions we have considered are those associated with the odd-parity irreducible representations (IRs) of the point group D2h, namely, those presented in Table 3.

In all cases \({\bf{d}}\left({\bf{k}}\right)={{\bf{d}}}^{* }({\bf{k}})\), the gap function is unitary and the nodal locations are defined by FS intersections with the high-symmetry lines of the BZ. Within this model, the nodal points are indicated by yellow dots in Extended Data Fig. 1a–c for \({B}_{1u}\), \({B}_{2u}\) and \({B}_{3u}\), respectively. For \({B}_{1u}\) symmetry, the FS is fully gapped. Although sharing the same number of independent nodes, the locations of the nodes are extremely different in the 3D Brillion zone for the \({B}_{2u}\) and \({B}_{3u}\) order parameters (Extended Data Fig. 1b,c).

Next, we project the normal-state FS onto the (0–11) plane oriented at an angle of 24° between the normal to the (0–11) plane and the crystal b axis (Extended Data Fig. 1d). The result is a (0–11) SBZ. The basis vectors on this (0–11) plane are \({{\bf{e}}}_{a}=\left(\mathrm{1,0,0}\right)\) and \({{\bf{e}}}_{{c}^{* }}=\left(0,\sin \theta ,\cos \theta \right)\), where \(\theta =24^\circ\). When an arbitrary vector of (a,b,c) is projected to the (0–11) plane, the projected vector is \(\left(\left(a,b,c\right)\cdot {{\bf{e}}}_{a},\left(a,b,c\right)\cdot {{\bf{e}}}_{{c}^{* }}\right)=(a,0.4b+0.91c)\). This occurs because any momentum k of the bulk BZ can be decomposed into momentum components parallel to the plane k|| and components perpendicular to the plane k⊥ of the surface. Then only k|| will contribute to the surface quasiparticle states, as k⊥ is no longer a conserved quantity; that is, the (001) quasiparticle states that are transformed into k⊥ states in the (0–11) plane no longer contribute. This is why the scale of q space and the size of the SBZ are both reduced when viewed at the (0–11) termination surface of UTe2.

Finally, we project the bulk nodes onto the (0–11) plane and obtain a k-space projected-nodal structure for order parameters \({B}_{1u}\), \({B}_{2u}\) and \({B}_{3u}\), respectively (Extended Data Fig. 1e–g). By definition, \({A}_{u}\) and \({B}_{1u}\) have no bulk or projected energy-gap nodes, so we consider them no further. However, at the (0–11) SBZ of UTe2, the projected-nodal locations of the bulk \({B}_{2u}\) order parameter are fundamentally different from those of the bulk \({B}_{3u}\) order parameter, as shown in Extended Data Fig. 1f,g, respectively.

Quasiparticle scattering interference in the QSB at the (0–11) surface of UTe2

We choose to work in the following basis, where U1/2 and Te1/2 denote, respectively, the two uranium and tellurium orbitals:

$${{\rm{\psi }}}^{+}\left({\bf{k}}\right)=({c}_{{U}_{1},{\bf{k}},\sigma }^{+},{c}_{{U}_{2},{\bf{k}},\sigma }^{+},{c}_{T{e}_{1},{\bf{k}},\sigma }^{+},{c}_{T{e}_{2},{\bf{k}},\sigma }^{+},{c}_{{U}_{1},-{\bf{k}},\bar{\sigma }},{c}_{{U}_{2},-{\bf{k}},\bar{\sigma }},{c}_{T{e}_{1},-{\bf{k}},\bar{\sigma }},{c}_{T{e}_{2},-{\bf{k}},\bar{\sigma }})$$

(11)

$${c}_{\alpha ,{\bf{k}},\sigma }^{+}=({c}_{\alpha ,{\bf{k}},\uparrow }^{+},{c}_{\alpha ,{\bf{k}},\downarrow }^{+})$$

(12)

$${c}_{\alpha ,{\bf{k}},\bar{{\boldsymbol{\sigma }}}}=({c}_{\alpha ,{\bf{k}},\downarrow },{c}_{\alpha ,{\bf{k}},\downarrow })$$

(13)

In this basis, the BdG Hamiltonian of a p-wave spin-triplet superconductor can be written as

$${H}_{{\rm{BdG}}}\left({\bf{k}}\right)={{\rm{\psi }}}^{+}\left({\bf{k}}\right)\left(\begin{array}{ll}{H}_{{\rm{UT}}{{\rm{e}}}_{2}}\left({\bf{k}}\right)\bigotimes {I}_{2}\qquad\Delta \left({\bf{k}}\right)\bigotimes {I}_{4}\\ {\Delta }^{+}\left({\bf{k}}\right)\bigotimes {I}_{4}\qquad\;-{H}_{{\rm{UT}}{{\rm{e}}}_{2}}^{* }\left(-{\bf{k}}\right)\bigotimes {I}_{2}\end{array}\right){\rm{\psi }}({\bf{k}})$$

(14)

where the order parameter for the putative p-wave superconductor is \(\Delta \left({\bf{k}}\right)={\Delta }_{0}i\left({\bf{d}}\cdot {\bf{\upsigma }}\right){\sigma }_{2}\), and In is an n × n identity matrix. In our analysis, we focus on the non-chiral order parameters: \({A}_{u}\), \({B}_{1u}\), \({B}_{2u}\) and \({B}_{3u}\). The d vectors used in calculations for each IR are provided in Table 3.

Table 3 Odd-parity irreducible representations of the crystal point symmetry group D2h and corresponding d vectors representations for the simple orthorhombic lattice model used throughout this Article

In our simulations, we hypothesize the following values: C0 = 0, C1 = 300 µeV, C2 = 300 µeV and C3 = 300 µeV. In this conventional model \({C}_{1}\), \({C}_{2}\) and \({C}_{3}\) are hypothesized to be the same as the UTe2 gap amplitude measured in the experiment. Although the relative intensity of these coefficients is not known a priori, we have checked that, while keeping the maximum gap constant, these coefficient values produce the same QPI features with only slight changes in wavevector length. Within this model, the unperturbed retarded bulk 3D Green’s function is given as

$${G}_{0}({\boldsymbol{k}},\omega )={[(\omega +i{\eta })I-{H}_{{\rm{BdG}}}({\boldsymbol{k}})]}^{-1}$$

(15)

with the corresponding unperturbed spectral function written as

$${A}_{0}({\boldsymbol{k}},\omega )=-1/\pi {Im}{G}_{0}({\boldsymbol{k}},\omega )$$

(16)

where η is the energy-broadening factor in the theory simulation.

Although obtaining the bulk Green’s function is straightforward, calculating the surface Green’s functions and spectral functions As(k,ω) is substantially more difficult. The complexity arises because the surface Green’s functions characterize a semi-infinite system with broken translational symmetry, and thus they cannot be calculated directly. Traditionally, they are obtained using heavy numerical recursive Green’s function techniques as in ref. 49. Here we use a simpler analytical technique, described in refs. 44,45,46, in which the surface is modelled using a planar impurity. When the magnitude of the impurity potential goes to infinity, the impurity splits the system into two semi-infinite spaces. Then only wavevectors in the (0–11) plane remain good quantum numbers. The effect of this impurity can be exactly calculated using the T-matrix formalism, which gives one access to the surface Green’s function of the semi-infinite system.

We model the effect of the surface using a planar-impurity potential, as in Extended Data Fig. 2, which is oriented parallel to the (0–11) crystal plane. In the presence of this impurity, the bulk Green’s function is modified to

$$G\left({{\bf{k}}}_{1},{{\bf{k}}}_{2},\omega \right)={G}_{0}\left({{\bf{k}}}_{1},\omega \right){\delta }_{{{\bf{k}}}_{1},{{\bf{k}}}_{2}}+{G}_{0}\left({{\bf{k}}}_{1},\omega \right)T\left({{\bf{k}}}_{1},{{\bf{k}}}_{2},\omega \right){G}_{0}\left({{\bf{k}}}_{2},\omega \right)$$

(17)

where the T matrix considers all-order impurity scattering processes. For a plane impurity localized at \(x=0\) and perpendicular to the x axis, the T matrix can be computed as

$$T\left({k}_{1y},{k}_{1z},{k}_{2y},{k}_{2z},\omega \right)={\delta }_{{k}_{1y},{k}_{2y}}{\delta }_{{k}_{1z},{k}_{2z}}[1-\hat{V}\int \frac{d{k}_{x}}{{L}_{x}}{G}_{0}\left({k}_{x},{k}_{1y},{k}_{1z},\omega \right)]^{-1}\hat{V}$$

(18)

with \({L}_{x}\) a normalization factor. Because the impurity potential is a delta function in x, the T matrix is independent of \({k}_{x}\) and depends only on \({k}_{y}\) and \({k}_{z}\).

We calculate the exact Green’s function one lattice spacing away from the planar-impurity potential, which converges precisely to the surface Green’s function as the impurity potential approaches infinity. This surface Green’s function can be obtained by performing a partial Fourier transform of the exact Green’s function expressed in equation (17):

$${G}_{s}\left({k}_{y},{k}_{z}\right)=\int \frac{d{k}_{1x}}{{L}_{x}}\int \frac{d{k}_{2x}}{{L}_{x}}G\left({k}_{1x},{k}_{y},{k}_{z},{k}_{2x},{k}_{y},{k}_{z},\omega \right){e}^{i{k}_{1x}x}{e}^{-i{k}_{2x}{x}^{{\prime} }}$$

(19)

where \(x={x}^{{\prime} }=\pm 1\).

Extended Data Fig. 3a–c is generated using the above (0–11) planar-impurity-potential formalism for the four-band model with B1u, B2u and B3u gap structures. In Extended Data Fig. 3, we present the surface spectral function As(k, E) for these order parameters in the (0–11) SBZ. In particular, the surface spectral function As(k, E) for B3u in the (0–11) SBZ is shown in Extended Data Fig. 3c. A hypothesized sextet of scattering wavevectors qi, i = 1–6 connecting regions of maximum intensity in As(k, 0) is overlaid. All plots show data for six energy levels, with the highest near the gap edge of \(|{\Delta}_{\text{UT}{{\rm{e}}}_{2}}|=300\) µeV.

We next describe how QPI scattering is possible given the putative protection of superconductive topological surface band quasiparticles against scattering in a topological superconductor. Formally, we can derive the spin-resolved quasiparticle surface spectral function as shown for a B2u and B3u QSB in Extended Data Fig. 4. The resulting surface spectral function can be clearly segregated into two spin-polarized bands in UTe2, one for each spin eigenstate. Although spin-flip and thus inter-spin-band scattering is proscribed, non-spin-flip or intra-spin-band scattering is allowed, thus allowing QPI of these quasiparticles.

Extended Data Fig. 5a,b depicts the projection of the bulk spectral function of order parameters \({B}_{2u}\) and \({B}_{3u}\) on the (0–11) surface. It should be noted that the resulting features correspond to regions identifiable from the 3D bulk FS as the projection of the bulk nodes onto the (0–11) surface, and these features are highlighted by yellow circles. Extended Data Fig. 5c,d depicts the surface spectral function As(k, 0) computed using the planar-impurity method44. It accounts for some bulk contributions but is dominated by new features that connect the projection of the bulk nodes to the SBZ; these new features correspond to the QSB of order parameters \({B}_{2u}\) and \({B}_{3u}\).

In Extended Data Fig. 5e,f, we consider (0–11) surface QPI featuring order parameters of \({B}_{2u}\) and \({B}_{3u}\) symmetry using the JDOS \(J\left({\boldsymbol{q}},0\right)\). The JDOS approximation \(J\left({\bf{q}},0\right)\) is a well-established technique to map out the geometries of the momentum-space band structures36. The JDOS approximation is based on the observation that if the surface spectral functions \({A}_{{\rm{s}}}\) at k and k + q are both simultaneously large, then \(J\left({\bf{q}},E\right)\) will be large, as q connects regions of large JDOS. This technique has been used to successfully interpret the experimental QPI data for high-temperature superconductors50,51, topological insulators52,53 and Weyl semimetals54,55.

Although \(J\left({\bf{q}},E\right)\) captures the dominant k-space quasiparticle scattering associated with the order-parameter symmetries, it does not consider spin-forbidden scattering processes and the underlying contributions from the bulk band structure as accurately as the \(N\left({\bf{q}},E\right)\) simulations presented in the main text. However, both \(J\left({\bf{q}},E\right)\) and \(N\left({\bf{q}},E\right)\) calculations reveal distinct scattering features.

We show the theoretical N(E) calculations for the UTe2 (0–11) surface with B2u and B3u gap symmetries in Extended Data Fig. 5g,h. Both gap symmetries show the indistinguishable bulk N(E) of a nodal p-wave superconductor (black curve). The N(E) at the surface (red curve) differs entirely between the two order-parameter symmetries in this model. For a B3u order parameter, the surface N(E) has a clear zero-energy peak; however, the surface N(E) due to a B2u order parameter has only reduced gap depth compared to bulk. In the experiment, we find intense zero-energy conductance, which appears most consistent with the (0–11) surface N(E) in the presence of B3u gap symmetry.

To further improve the comparison between the QPI simulations and the experimental QPI data, we consider of the q-space sensitivity of our scan tip in the QPI simulations. The QPI simulations \(N\left({\bf{q}},E\right)\) for the B2u and B3u order parameters are shown in Extended Data Fig. 6a,b, which shows very strong intensities near the high-q region. In experimental data, however, the intensity near the high-q regions that represent the shortest distances in r space decays rapidly due to the finite radius of the scan tip. We estimate the actual q-space intensity decay radius from a Gaussian fit to the power spectral density of the relevant T(q) image. Subsequently, we apply a 2D Gaussian function of the following form to the QPI simulations \(N\left({\bf{q}},E\right)\), reflecting the effects of the finite circular radius or ‘aperture’ of the scan tip:

$$f\left({q}_{x},{q}_{y}\right)=A\exp \left(-\left(\frac{{\left({{\boldsymbol{q}}}_{x}-{{\boldsymbol{q}}}_{{x}_{0}}\right)}^{2}}{2{\sigma }_{x}^{2}}+\frac{{\left({{\boldsymbol{q}}}_{y}-{{\boldsymbol{q}}}_{{y}_{0}}\right)}^{2}}{2{\sigma }_{y}^{2}}\right)\right)$$

(20)

where the amplitude \(A=1.75\times {10}^{-5}\), the centre coordinates \(\left({q}_{{x}_{0}},{q}_{{y}_{0}}\right)=(\mathrm{0,0})\) and the standard deviation \({\sigma }_{x}={\sigma }_{y}=3.68\pi /{c}^{* }\). Upon applying this 2D ‘aperture’ filter in Extended Data Fig. 6a,b, we derive the \(N({\bf{q}},E)\) in main text Fig. 4g,i.

To evaluate the effect of impurity strength on the QPI calculations, we performed superconductive topological surface band QPI simulations using local impurity potentials of V = 0.07, 0.2, 0.5 and 1 eV potentials and found that the predictions using different scattering impurity potentials lead to highly consistent scattering wavevectors (Extended Data Fig. 6c–f). Varying the scattering potentials only changes relative amplitudes at different wavevectors; when the scattering potentials increase, the scattering wavevectors caused by the surface state become more intense. We chose V = 0.2 eV because the QPI simulations calculated using this scattering potential are most consistent with the relative QPI intensities observed experimentally. The scientific conclusion that QPI in the superconductive topological surface state of UTe2 is consistent with B3u bulk pairing symmetry remains unchanged when using scattering potentials ranging from 0.07 to 1 eV, as presented above.

SABS in unconventional superconductors

The SABS and concomitant zero-bias conductance peaks due to π phase shifts have been extensively studied for decades, particularly in high-temperature superconductors17,56,57,58,59. In d-wave superconductors such as the cuprates, the π phase shift of the pair potential occurs universally when the angle between the crystal axis of the superconductors and the lobe direction of d-wave pair potential is nonzero. This phase shift leads to the formation of SABS due to Andreev reflection. These SABS manifest as zero-bias conductance peaks in tunnelling spectroscopy, a hallmark feature widely observed and investigated in the cuprate high-temperature superconductors.

Although never observed experimentally in a spin triplet superconductor, SABS should emerge in 3D p-wave ITSs, where they are often described as superconducting topological surface states. These SABS have a somewhat distinct physical origin from those in d-wave systems because in odd-parity superconductors, there is a universal π phase shift of the superconducting order parameter at all surfaces, independent of the angle between the crystal axis and the direction of the phase of the superconducting order parameter.

Alternative gap function and impurity potential

Owing to the body-centred orthorhombic crystal symmetry of UTe2, basis functions other than those presented in the main text and above are allowed. To consider alternative basis functions, we add additional, symmetry-allowed, terms to the d vectors as described in ref. 8. For the nodal, single-component order parameters, we then use the d vectors featured in Table 4 with \({C}_{0}=0\), \({C}_{1}={C}_{2}={C}_{3}=0.225\) \(\text{meV}\) and \({C}_{4}={C}_{5}={C}_{6}=0.15\) \(\text{meV}\).

Table 4 The d vector representations for the body-centred orthorhombic lattice model

To establish that the conclusions derived in the main text would be unchanged if these alternative d vectors were used, we calculate the bulk projected spectral function A0(k, E), surface spectral function As(k, E) and \(J\left({\bf{q}},E\right)\) using these alternative triplet d vectors. These data are presented in Extended Data Fig. 7 for \(E=0\). The nodal pattern highlighted with yellow dashed circles in Extended Data Fig. 7a,b can be directly compared to Extended Data Fig. 5a,b. The alternative d vectors have a very similar nodal pattern when projected to the (0–11) plane, and thus the QSBs occupy similar regions of the projected SBZ. This can be seen in Extended Data Fig. 7c,d, in which we plot As(k,0). From comparison with Extended Data Fig. 5c,d, we see clearly that the QSBs calculated using either the main text d vector or these alternative d vectors are nearly identical. The resulting \(J\left({\bf{q}},E\right)\), is presented in Extended Data Fig. 7e,f for order-parameter symmetries B2u and B3u, respectively. Using the same quasiparticle broadening parameter as in Extended Data Fig. 5e,f, \(\eta =30\) μeV; but now, with these alternative d-vector terms, we see that the \(J\left({\bf{q}},E\right)\) QPI patterns predicted for each order parameter have the same key features.

Andreev conductance a(r,V) of QSB quasiparticles

A key consideration is the role of QSB-mediated Andreev conductance across the junction between p-wave and s-wave superconductors (Extended Data Fig. 8). Most simply, a single Andreev reflection transfers two electrons (holes) between the tip and the sample. Based on an S-matrix approach, the formula to compute the Andreev conductance of the s-wave–insulator–p-wave model is

$$a\left(V\;\right)=\frac{8{\pi }^{2}{t}_{{\rm{eff}}}^{\;4}{e}^{2}}{h}\sum _{n}\frac{\left\langle {\phi }_{n}|{P}_{h}|{\phi }_{n}\right\rangle \left\langle {\phi }_{n}|{P}_{e}|{\phi }_{n}\right\rangle }{{\left({eV}-{E}_{n}\right)}^{2}+{\pi }^{2}{t}_{{\rm{eff}}}^{\;4}{\left[\left\langle {\phi }_{n}|{P}_{h}|{\phi }_{n}\right\rangle +\left\langle {\phi }_{n}|{P}_{e}|{\phi }_{n}\right\rangle \right]}^{2}}$$

(21)

Here, |\({\phi }_{n}\rangle\) is the projection of the nth QSB eigenfunction onto the top UTe2 surface, \({P}_{e}\) and \({P}_{h}\) are the electron and hole projection operators acting on the UTe2 surface, and V is the bias voltage. Thus, in principle, and as outlined in ref. 35, superconductive scan tips can be employed as direct probes of QSBs, with tip-sample conductance mediated by Andreev transport through the QSB.

Distinguish between Andreev tunnelling and Josephson tunnelling

Determining whether the physical origin of the zero-bias conductance is due to Josephson or Andreev tunnelling is important. However, Josephson currents are undetectable in all Nb/UTe2 junctions that we have studied. This can be demonstrated by comparing the zero-bias (Andreev) conductance a(0) versus junction resistance R on the same plot with the maximum possible zero-bias conductance g(0), which could be generated by the Josephson effect (as shown in Supplementary Fig. 6 of ref. 35). First, at high R, the intensity of measured a(0) of Nb/UTe2 junctions is orders of magnitude larger than it could possibly be due to Josephson currents (here exemplified by measured Nb/NbSe2 Josephson effect zero-bias conductance60 that itself should be at least five times larger than any that could exist in Nb/UTe2). Second, measured a(0) for Nb/UTe2 first grows linearly with falling R but then diminishes steeply as R is reduced further. By contrast, zero-bias conductance due to Josephson currents g(0) must grow rapidly and continuously as 1/R2, as exemplified in the Nb/NbSe2 g(0) data60. These facts (Supplementary Fig. 6 of ref. 35) demonstrate the absolute predominance of Andreev tunnelling and the non-observability of Josephson currents between Nb electrodes and the UTe2 (0–11) termination surface.

Normal-tip and superconductive-tip study of QSBs

Motivated by the presence of dominant finite density of states at zero energy as \(T\to 0\) and by the consequent hypothesis that a QSB exists in this material, we searched for its signatures using a non-superconductive tip, at voltages within the superconducting energy gap, and identified unique features resulting from QSB scattering interference. The typical NIS tunnelling conductance of the UTe2 superconducting state measured using a non-superconductive tip is exemplified in the inset to Extended Data Fig. 9b. At the (0–11) surface of superconducting UTe2 crystals, almost all states inside the superconducting gap \({|E|} < {\Delta }_{0}\) show residual, ungapped density of states. A combination of impurity scattering and the presence of a QSB on this crystal surface are expected for a p-wave superconductor. Both types of these unpaired quasiparticles should contribute to conductance measurements performed within the superconducting gap using a non-superconductive scan tip. To visualize the scattering interference of QSB quasiparticles, we focus on a 40-nm-square FOV (Extended Data Fig. 9a) for conventional normal-tip differential conductance \({{\rm{d}}I}/{{\rm{d}}V}{|}_{{\rm{NIS}}}({\bf{r}},V)\) at T = 280 mK and at a junction resistance of R = 5 MΩ. Although the QPI inside the superconducting gap shows some evidence of the QSB in UTe2, its weak signal-to-noise ratio owing to the dominant finite density of states for \(\left|E\right|\le {\Delta }_{0}\) implies that conventional dI/dV|NIS q,V) spectra are inadequate for precision application of detecting and quantifying the QPI of the QSB in UTe2.

Thus, we turned to a new technique by using superconductive tips to increase the signal-to-noise ratio of QSB quasiparticle scattering. Recent theory for the tunnel junction formed between an s-wave superconductive scan tip and a p-wave superconductor with a QSB within the interface35 reveals that the high density of QSB quasiparticles allows efficient creation/annihilation of Cooper pairs in both superconductors, thus generating intense Andreev differential conductance a(r, V) ≡ \({{\rm{d}}I}/{{\rm{d}}V}{\ |}_{{\rm{A}}}({\bf{r}},V)\). This is precisely what is observed when UTe2 is studied by superconductive Nb-tip STM at T = 280 mK, as evidenced by the large zero-energy conductance peak around a(r, 0) (inset to Extended Data Fig. 9d). Visualization of a(r, 0) and its Fourier transform a(q, 0), as shown in Extended Data Fig. 9d, reveals intense conductance modulations and a distinct QPI pattern. Comparing g(q, 0) in Extended Data Fig. 9b and a(q, 0) in Extended Data Fig. 9d reveals numerous common characteristics, thus demonstrating that use of a(q, V) imaging yields equivalent QPI patterns as g(q, V) imaging but with a greatly enhanced signal-to-noise ratio. This is as expected because spatial variations in the intensity of a(r, V) are controlled by the amplitude of QSB quasiparticle wavefunctions as in equation (21), so spatial interference patterns of the QSB quasiparticles will become directly observable in a(r, V). Thus, visualizing spatial variations in a(r, V) and their Fourier transforms a(q, V) enables efficient, high-signal-to-noise-ratio exploration of QSB quasiparticle scattering interference phenomena at the surface of UTe2.

Independent QSB visualization experiments

To confirm that the QPI of the QSB is repeatable, we show two additional examples of the Andreev QPI \(a({\bf{q}},0)\) from two different FOVs in Extended Data Fig. 10. The QPI maps \(a({\bf{q}},0)\) are measured at zero energy, where the Andreev conductance is most prominent. The two QPI \(a({\bf{q}},0)\) maps in Extended Data Fig. 10a,b show vividly the same sextet of scattering wavevectors qi, i = 1–6 reported in the main text and further confirm the signatures of a B3u QSB in UTe2. In particular, repeated measurements of the \({{\bf{q}}}_{1}\) wavevector exclusively both within the superconducting energy gap and at T = 280 mK support the presence of a superconducting order parameter with B3u symmetry, as this is the only order parameter that allows spin-conserved scattering at \({{\bf{q}}}_{1}\). These two QPI maps are measured independently in two different FOVs and at two different scanning angles (Extended Data Fig. 10c,d).

Origin of the scattering wavevector \({{\bf{q}}}_{1}\)

The interaction with uniform superconductivity of the UTe2 pre-existing charge density wave (CDW) or of the consequent pair density wave (PDW), both occurring with the same wavevector Q = q6, cannot induce either a CDW or a PDW at Q/2. This is ruled out by Ginzburg–Landau theory61. As to the appearance of a new fundamental PDW at a q1, this has been ruled out previously by direct search for energy-gap modulations at that wavevector13.

The emergence of q1 scattering intensely in the superconducting state of UTe2 occurs naturally because this wavevector arises from Bogoliubov quasiparticle scattering between symmetry-imposed superconducting nodes of the B3u order parameter34. In the normal state, scattering between FSs at this wavevector may also occur, but it is not predominant.

Notably, the superconducting gap nodes of the B3u order parameter coincide with the location of the normal-state FS nesting points. Consequently, the QPI wavevectors observed in the superconducting state of UTe2 (Fig. 3d) coincide with the normal-state FS nesting vectors. This is not necessarily the case in other superconductors such as Sr2RuO4, where the Bogoliubov QPI scattering wavevectors are entirely different from the normal-state FS nesting vectors because of the locations of the nodes in that material43.