Study design and sampling
This study was a cross-sectional design, assessed at the University of Bologna Sports Sciences laboratory in a room with 19.5 °C and 56% humidity. All the participants were players of the Virtus Bologna basketball Club, divided into two age categories: Under 17, composed of 16 players with 8.99 ± 2.62 years of experience (56.44% of life) and 12 h of training per week; Under 19, consisted of 14 players with 12.174 ± 3.07 years of experience (68.06% of life) and 14 h of training per week. A parent or legal guardian and adult players were informed of all experimental scopes, risks and privacy policies, and provided a written informed consent for both study participation and publication of identifying information in an online open-access publication. However, with respect to participant privacy, investigators provided data and results with no information that could lead to participants identification, deleting sensitive data such as name, surname, birthdate and/or personal images. The experiment was assessed in accordance with Helsinki ethical guidelines and approved by the bio-ethical University of Bologna committee (25,027, March 13, 2017).
The sample size was estimated a Priori to reach a statistical power of 0.8 with a type I error of 5% for a multiple Linear regression F test for partial correlation, with 12 covariates (number of measured parameters), with the effect size (squared partial correlation) equals to 0.5. The cross-validation was performed under the same conditions after 30 days.
Anthropometry
Stature was measured with a validated stadiometer (Health o Meter PORTROD, 9500 West 55th Street, McCook, IL, USA) by 1 mm of precision, according to Lohman27. Circumferences and skinfold thicknesses were detected on the right-body at standardized body sites41,42,43,44. Circumferences were measured twice at each body site with an elastic tape (Seca 201, Hammer Steindamm, Hamburg, Germany) for arm (95% CI ICC: 0.998, 0.999), thigh (95% CI ICC: 0.999, 0.999) and calf (95% CI ICC: 0.998, 0.999), whereas skinfold thicknesses were detected twice with a validated calliper (Lange, Beta Technology, Santa Cruz, CA, USA) at biceps (95% CI ICC: 0.917, 0.982), triceps (95% CI ICC: 0.965, 992), subscapular (95% CI ICC: 0.941, 0.988), sopra-iliac (95% CI ICC: 0.976, 0.995), sopra-spinal (95% CI ICC: 0.959, 0.991), thigh (95% CI ICC: 0.967, 0.993), medial calf (95% CI ICC: 0.973, 0.994), and the mean values were used for analysis. Table 4 shows the technical error of measurement (TEM) and coefficient of reliability for all anthropometrical variables.
Table 4 Technical error and reliability of measurements.Bio-impedance analysis (BIA)
Total body tissue resistance (R) and reactance (Xc) were detected by a BIA analyser (BIVA PRO, Akern, Florence, Italy) according to validated standards45, at the right side of the body, with the upper-body proximal electrode placed at wrist joint mid-point and distal electrode five centimetres farer (close to metacarpal bones), while the lower-body proximal electrode placed at ankle joint mid-point and distal electrode five centimetres farer (close to metatarsal bones). The analyser was calibrated before the evaluation according to reference: R desired 383 ± 10 Ω and observed 384.2 Ω (∆<1%), while Xc desired 45 ± 5 Ω and observed 44.5 Ω (∆=1%). Participants were asked to respect experimental conditions such as 4-hour fasting, 12 h of resting, and at least 24 h of no alcohol assumption. Each assessment has been taken twice and the relative technical error of measurement (TEM) for R and Xc is ~ 5%.
The total body water (TBW) and intracellular body water (ICW) were estimated by Matias and colleagues’ method31, and the extracellular body water was computed as TBW – ICW.
Air displacement plethysmography (ADP)
Both body mass (BM) and body volume (BV) were measured using the Bod Pod GS-X (Cosmed, Rome, Italy). The ADP was calibrated before the evaluation day, in accordance with the manufacturer’s instructions. The weight balance system worked with a precision of 0.01 kg and an error of less than 0.1%. An auto-calibration with six runs was assessed, with an average value of 45.025 ± 0.011 (error ~ 0.1%). Finally, the volume of the participant chamber was calibrated with an average value of 48.506 ± 0.008 (error ~ 0.01%). Each participant was tested twice, and if the system spotted a difference greater than 150 mL, an additional evaluation was required (95% CI ICC: 0.996, 0.999; relative TEM = 0.35%, reliability = 99.94%). All participants were instructed to wear a stretch nylon swimsuit and a Cosmed swimming cup and maintain a standardized posture during the evaluation. The volume thoracic has (VTG) was measured using standard pulmonary plethysmography or estimated by Crapo and collaborators method if it was not successfully obtained46. The surface area artefact (SAA) was calculated by Du Bois and Du Bois47. The body volume was finally computed by Dempster and Aitkens30 as follows:
$$\:BV\:\left[L\right]={BV}_{measured}+\left(0.4\text{*}VTG\right)-SAA\:$$
(1)
where \(\:SAA={BM}^{0.425}*{stature}^{0.725}*71.84.\)
The body density (d) was then obtained as \(\:\raisebox{1ex}{$BM$}\!\left/\:\!\raisebox{-1ex}{$BV\left[\frac{kg}{L}\right]$}\right..\)
Body composition
Many models were used to estimate Body fat (BF) and fat-free mass (FFM), according to previous results:
$$\:BF=\left(\frac{4.57}{d}-4.142\right)\text{*}100$$
(2)
Brozek48:
$$\:BF=\left(\frac{4.95}{d}-4.5\right)\text{*}100$$
(3)
2-C Siri 44:
$$\:BF=\left(2.118\text{*}BV\right)-\left(0.78\text{*}TBW\right)-\left(1.351\text{*}BM\right)$$
(4)
3-C Siri 44:
$$\:BF=\left(\frac{{C}_{1}}{d}-{C}_{2}\right)\text{*}100$$
(5)
Lohman 3636:
where \(\:{C}_{1}\) and \(\:{C}_{2}\) are constant based on age.
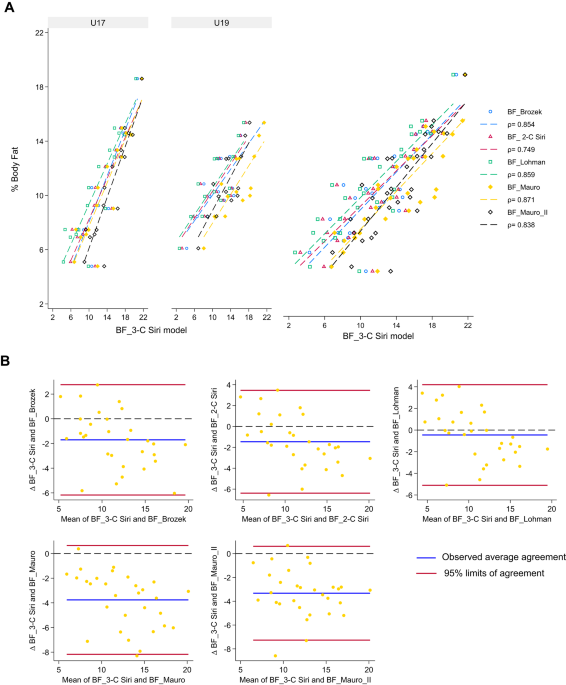
According to Wang and colleagues8, the 3-C Siri model has been considered as the reference for its high level of concordance with the atomical 6-C model (relative TEM = 3.43%, reliability = 99.54%). However, the higher level of BF (\(\:{f}_{1}\)) and FFM (\(\:{f}_{0}\)) and their relative densities (\(\:{d}_{1}\) and \(\:{d}_{0}\)) have been recorded and then applied to customize standards for adolescent basketball players, into the general formula:
$$\:BF=\frac{{d}_{1}{d}_{0}}{d}\:\left(\frac{{f}_{1\:}-{f}_{0}}{{d}_{0}-{d}_{1}}\right)-\frac{{d}_{1}{f}_{1}-{d}_{0}{f}_{0}}{{d}_{0}-{d}_{1}}$$
(6)
Where \(\:{d}_{0}\) (density of FFM) has been computed by removing from BV the volume associated with fat mass, obtained as BM/\(\:{d}_{1}\) where density was constant at 0.9 kg/L, and by dividing the FFM by fat-free volume, obtained as BV-fat volume.
In addition, the uncertainty of propagation has been computed as follows:
$$\:{\sigma\:}_{f}=\sqrt{{a}^{2}{\sigma\:}_{BV}^{2}+{b}^{2}{\sigma\:}_{BM}^{2}-2ab{\sigma\:}_{BV\:BM}}$$
(7)
Where a and b are scalars, σ is the standard deviation of the parameter and σBV BM is the covariance of measured parameters. The error obtained is then divided by BM to obtain the desired percentage.
Statistical analysis
Central tendency and dispersion of variables have been quantified by mean and standard deviation. The technical error of repeated measurements (TEM) has been computed as \(\:\sqrt{\raisebox{1ex}{$\sum\:{\varDelta\:}^{2}$}\!\left/\:\!\raisebox{-1ex}{$2n$}\right.}\) and its relative effect as (TEM/mean) *100, while the coefficient of reliability as 1-(TEM2/std2). Linear correlation has been measured by the Pearson product-moment coefficient (ρ). Variables and residuals’ distributions have been checked graphically and by Kolmogorov-Smirnov, Cramer-von Miles and Anderson-Darlin tests. The stepwise procedure has been performed to select the best regressors at 5% type I error probability(both for entry and removal level), with Bonferroni adjustment method. For meeting general linear model assumptions, the error sphericity has been tested by the White method, whereas tests on residuals such as Cook distance (with cut-off settled at 4/n), DFBETAS and DFFITS have been assessed for excluding outliers and leverage points. The variance inflation factor (VIF) was computed to account for multicollinearity, and a value lower than 10 was considered acceptable. To evaluate the goodness of fit, many indexes such as the adjusted-R2, Akaike and Bayesian information criteria, and Bland and Altman’s49 limit of agreement have been implemented. Also, Lin’s concordance correlation coefficient50 given by the ratio of the Pearson correlation coefficient (a measure of precision) and the bias correction factor (a measure of accuracy) have been used. To compare variables between age categories, the one-way ANOVA has been assessed. To assess cross-validation, a paired sample t-test compared the mean values between the reference technique and new method, within cross-validated sample. Then, Lin’s method was applied to measure precision, accuracy and bias. The alpha level was settled at 0.05 for each hypothesis test. The Microsoft Excel (version 2024, Windows edition) software was used to collect and gather data, while both SAS (version 9.4, Windows edition) and STATA (version SE 18, Windows edition) performed the statistical analysis.