In Fig. 1 we present the field resilient gralmonium qubit, fabricated from a single layer of grAl (cf. Fig. 1a), with a critical field on the order of Bc ~ 6 T39. We use a 20 nm thick grAl film with a sheet inductance of L□ = 0.75 nH/□ (resistivity ρ = 2000 μΩ cm) to design all circuit elements (cf. “Methods”). We galvanically couple a 1 mm long stripline readout resonator to the qubit circuit, consisting of a superinductor, a geometric finger capacitance and a grAl nanojunction. Implemented by a ~(20 nm)3 grAl volume, the nanojunction offers a sinusoidal current-phase relation similar to conventional Al/AlOx/Al JJ46, while exposing a minute cross-section to Fraunhofer interference. To reduce the sensitivity to magnetic flux fluctuations perpendicular to the thin film, we implement a gradiometric design48 with two flux loops (ocher & violet in Fig. 1a) containing fluxes Φ1, Φ2, respectively. The equivalent circuit diagram in Fig. 1b can be mapped to the standard fluxonium Hamiltonian
$$H=4{E}_{{{\rm{C}}}}{\hat{n}}^{2}+\frac{1}{2}{E}_{{{\rm{L}}}}{\left(\hat{\varphi }-2\pi \frac{{\Phi }_{{{\rm{ext}}}}}{{\Phi }_{0}}\right)}^{2}-{E}_{{{\rm{J}}}}\cos \hat{\varphi }\,,$$
(1)
where \({E}_{{{\rm{L}}}}={({\Phi }_{0}/2\pi )}^{2}/{L}_{{{\rm{q}}}}\), EC = e2/2C, EJ = IcΦ0/2π and Φ0 = h/2e. Here, \(\hat{n}\) represents the number of Cooper pairs and \(\hat{\varphi }\) is the phase difference across the junction. Due to the low intrinsic capacitance of the nanojunction, the qubit charging energy EC is dominated by the interdigitated capacitor C46. For the gradiometric circuit, the effective qubit inductance is given by \({L}_{{{\rm{q}}}}=\frac{{L}_{1,{{\rm{s}}}}{L}_{2}+{L}_{2}{L}_{3}+{L}_{3}{L}_{1,{{\rm{s}}}}}{{L}_{1,{{\rm{s}}}}+{L}_{3}}\) with L1,s = L1 + Ls, and the effective external flux is
$${\Phi }_{{{\rm{ext}}}}={\Phi }_{\Delta }-\alpha {\Phi }_{\Sigma }\,.$$
(2)
Here, \({\Phi }_{\Sigma /\Delta }=\frac{{\Phi }_{{{\rm{ext,1}}}}}{2}\pm \frac{{\Phi }_{{{\rm{ext,2}}}}}{2}\) denote the mean and difference of fluxes in the two loops, respectively, and \(\alpha=\frac{{L}_{1,{{\rm{s}}}}-{L}_{3}}{{L}_{1,{{\rm{s}}}}+{L}_{3}}\) is the inductance asymmetry. In our gradiometric design, the magnetic flux susceptibility is reduced by a factor of Φext,1/ΦΔ = 4.6 with α ≈ 0 (cf. Supplementary II).
Fig. 1: Gradiometric gralmonium qubit resilient to Tesla magnetic field.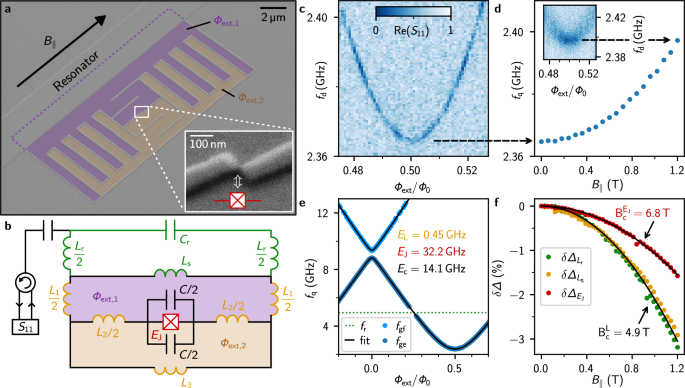
a False-colored scanning electron microscope (SEM) image of the qubit circuit, galvanically coupled to the readout resonator. The device consists of a 20 nm thick single layer of grAl. The colored regions (ocher & violet) illustrate the 10% mismatched areas of the two flux loops in the gradiometric design48, which result in an effective flux bias Φext in perpendicular magnetic field B⊥ (cf. Eq. (2)). Inset: zoom-in on the ~20 nm wide grAl nanojunction of the qubit (cf. ref. 46). b Circuit schematic for the gradiometric qubit depicted in a: the nanojunction (red) is shunted by an interdigitated capacitor and two flux loops (ocher & violet) with inductances L1 + Ls and L3, respectively. The inductance shared between the loops is L2. The qubit is inductively coupled via Ls to the readout resonator (inductance Lr, capacitance Cr) for which we measure the single-port reflection coefficient S11. c Two-tone (TT) spectroscopy at the half flux sweet spot Φext = Φ0/2 in B∥ = 0 T. d Increase of the sweet spot qubit frequency in magnetic field up to 1.2 T. Inset: TT-spectroscopy in B∥ = 1.2 T. e Qubit spectrum: ground to excited (fge in dark blue markers) and ground to second-excited (fgf in light blue markers) state transitions extracted from TT-spectroscopy. From a fit (black line) to the fluxonium Hamiltonian (Eq. (1)), we obtain EJ/h = 32.2 GHz (i.e., critical current Ic = 64.9 nA), Ec/h = 14.1 GHz (C = 1.37 fF) and EL/h = 0.454 GHz (Lq = 360 nH). f Suppression of the grAl superconducting gap Δ in magnetic field. The red and orange markers, corresponding to the qubit nanojunction and inductor superconducting gaps (\({\Delta }_{{E}_{{{\rm{J}}}}}\), \({\Delta }_{{L}_{{{\rm{q}}}}}\)), are obtained from fitted EJ and EL values (cf. e) at each magnetic field. The capacitance C is fixed to the fit value obtained in B∥ = 0 T. The green markers are obtained from the shift of the readout resonator frequency fr(B∥). The black lines show fits to the field dependence of the superconducting gap, indicating a 40% higher critical field for the nanojunction.
From two-tone (TT) spectroscopy at half flux bias Φ = Φ0/2 shown in Fig. 1c, we determine a qubit frequency of fq(Φ0/2) = 2.365 GHz in zero field, B∥ = 0. Remarkably, as shown in Fig. 1d, tracking the sweet spot qubit frequency in magnetic field reveals only a 1% increase (32 MHz) up to 1.2 T, illustrating the compatibility of the gradiometric gralmonium qubit with high magnetic fields. The spectroscopy data in 1.2 T is blurred compared to zero field due to low-frequency flux noise, likely from vibrations of the sample holder inside the vector magnet (cf. Supplementary I). Figure 1e shows the gralmonium spectrum up to 13 GHz, extracted from TT spectroscopy. A joint fit of the qubit transitions \(\left\vert \,{\mbox{g}}\,\right\rangle \to \left\vert \,{\mbox{e}}\,\right\rangle\) and \(\left\vert \,{\mbox{g}}\,\right\rangle \to \left\vert \,{\mbox{f}}\,\right\rangle\) to a numerical diagonalization of Eq. (1) yields typical fluxonium parameters: EJ/h = 32.2 GHz, Ec/h = 14.1 GHz and EL/h = 0.454 GHz.
To assess the effect of the magnetic field on the fluxonium parameters, we measure the qubit ground to excited transition frequency fge near the half- and zeroflux sweet spots at each B∥, using TT spectroscopy (similar to Fig. 1c). We fit fge to Eq.(1) using the field independent capacitance C = 1.37 fF obtained in zero field. From the fitted parameters, using EJ ∝ Δ(B∥) and Lkin ∝ 1/Δ(B∥), we extract the magnetic field suppression of the superconducting gap in the superinductor (\(\delta {\Delta }_{{L}_{{{\rm{q}}}}}\)) and nanojunction (\(\delta {\Delta }_{{E}_{{{\rm{J}}}}}\)), as shown in Fig. 1f. The suppression of the resonator superconducting gap (\(\delta {\Delta }_{{L}_{{{\rm{r}}}}}\)) is independently obtained by fitting the resonance frequency shift \({f}_{{{\rm{r}}}}\propto 1/\sqrt{{L}_{{{\rm{kin}}}}}\). Interestingly, the nanojunction has an even higher field resilience than the grAl resonator and superinductor. We fit the relative gap suppression to \(\sqrt{1-{({B}_{\parallel }/{B}_{{{\rm{c}}}})}^{2}}\)49 and obtain a critical field \({B}_{{{\rm{c}}}}^{{E}_{{{\rm{J}}}}}=6.8\,{{\rm{T}}}\) for the nanojunction and \({B}_{{{\rm{c}}}}^{{{\rm{L}}}}=4.9\,{{\rm{T}}}\) for the resonator and qubit inductance. The fact that \({B}_{{{\rm{c}}}}^{{E}_{{{\rm{J}}}}} > {B}_{{{\rm{c}}}}^{{{\rm{L}}}}\) indicates that possible Fraunhofer interference in the nanojunction plays a minor role. The higher critical field of the nanojunction is not understood and could be due to its reduced dimensions, similar to ref. 50.
We quantify the quantum coherence of the gralmonium in field by performing time-domain measurements at the half flux sweet spot, as summarized in Fig. 2. Remarkably, the energy relaxation time T1 and Hahn echo coherence time T2E remain robust in fields up to 1.2 T, the upper limit of our vector magnet (cf. Fig. 2a). The Ramsey coherence time T2R decreases from a maximum of T2R = 1.5 μs to T2R = 0.7 μs in fields above 1 T. We attribute this to an increase of low frequency flux noise, which stems from global flux variations introduced by vibrations and activated vortices in the vector magnet51, or from local flux noise, possibly from spins clusters38.
Fig. 2: Qubit coherence in magnetic field: signatures of environmental spin polarization.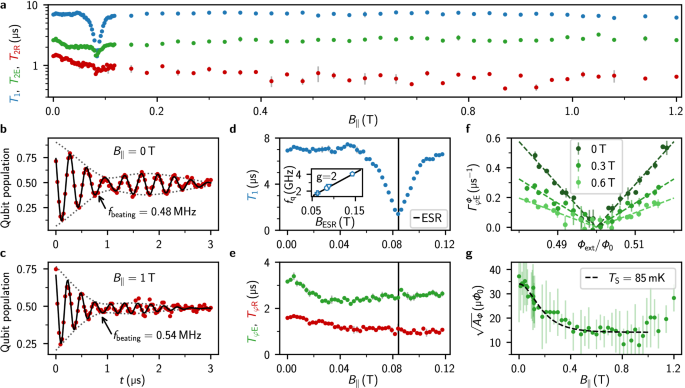
a Energy relaxation time T1, Ramsey and echo coherence time, T2R and T2E respectively, of the gradiometric gralmonium in magnetic field up to 1 T. b, c Ramsey fringes measured in B∥ = 0 T and B∥ = 1 T, respectively. A two-frequency fit (black line) indicates a similar beating pattern (dotted envelope) for both magnetic fields. d Energy relaxation T1 up to 120 mT: similarly to observations on resonators39–41, the drop in T1 suggests coupling to the electron spin resonance (ESR) of paramagnetic impurities of unknown origin. Inset: The fields BESR = hfq/gμB at which the ESR matches different qubit frequencies in different cooldowns, correspond to the expectation for a spin s = 1/2 ensemble with gyromagnetic factor g = 2 (black line). Note that we use the same device for which the qubit frequency changes between cooldowns (cf. ref. 46). e Dephasing times TφR, TφE remain unaffected by the ESR. f Flux noise echo dephasing rate \({\Gamma }_{\varphi \,{\mbox{E}}\,}^{\Phi }\) in the vicinity of the sweet spot for three in-plane magnetic fields. Dashed lines show fits to Eq. (3). g Flux noise amplitude \(\sqrt{{A}_{\Phi }}\) in magnetic field with fit to Eq. (4), corresponding to a spin freezing with a spin temperature of TS = 85 mK. In all panels, the error bars represent the standard deviation obtained from successive measurements.
The grAl nanojunction exhibits critical current fluctuations, as evidenced by a 0.5 MHz toggling of the qubit frequency and a corresponding beating pattern in Ramsey fringes at zero field (cf. Fig. 2b). As demonstrated in ref. 46, these fluctuations are inconsistent with transverse coupling to a fixed frequency TLS, but originate from fluctuations of the nanojunction energy, potentially arising from structural defects, charge noise, or paramagnetic impurities. This issue is also relevant for standard Al/AlOx/Al tunnel JJs30,52. We leverage the gradiometric gralmonium’s field resilience to test the magnetic susceptibility of critical current noise, showing in Fig. 2c that a 1 T in-plane magnetic field does not suppress the discrete fluctuations of the Josephson energy. This observation excludes magnetically susceptible sources, such as a local spin environment, as the origin of these fluctuations. Further experiments, such as electric field bias or mechanical strain on the substrate32,53 or spin-locking TLS spectroscopy54, are required to identify their cause.
We observe a dip in the energy relaxation time at the magnetic field where the electron spin resonance (ESR) matches the qubit frequency hf = gμBB (cf. Fig. 2d). This ESR resonance does not impact the dephasing times TφR, TφE (cf. Fig. 2e), as expected in the limit of a coupling strength much smaller than the qubit linewidth55. By exploiting ΔEJ ~ GHz changes in the nanojunction energy after thermal cycling, we change the qubit frequency of the same device, allowing measurements of the ESR-resonant field BESR across multiple qubit frequencies at the half flux sweet spot (inset of Fig. 2d). The linear trend of the extracted magnetic fields BESR aligns with the prediction for a g = 2 spin s = 1/2 ensemble, identifying a paramagnetic spin ensemble coupled to our qubit.
Figure 2f illustrates the flux dependence of the Hahn echo flux noise dephasing rate, \({\Gamma }_{\varphi \,{\mbox{E}}\,}^{\Phi }\), near the sweet spot for three in-plane magnetic fields (B∥ = 0, B∥ = 0.3 T, B∥ = 0.6 T). Away from the sweet spot, we observe a Gaussian contribution in the Hahn echo decay curve, consistent with commonly observed 1/f flux noise27,28,29,30,31,38,56. We extract \({\Gamma }_{\varphi \,{\mbox{E}}\,}^{\Phi }\) from the flux-dependent Gaussian envelope \({e}^{-{({\Gamma }_{\varphi {\mbox{E}}}^{\Phi }t)}^{2}}\), on top of a purely exponential decay \({e}^{-({\Gamma }_{1}/2+{\Gamma }_{\varphi {\mbox{E}}}^{{{\rm{const}}}})t}\), extracted at Φ = Φ0/2. The flux-independent term \({\Gamma }_{\varphi \,{\mbox{E}}}^{{\mbox{const}}\,}\) may originate from critical current noise or photon shot noise; in the latter case, the residual photon number is \(\bar{n}=0.27\), corresponding to an effective temperature of 150 mK, in agreement with the qubit temperature (cf. Supplementary I). Interestingly, the flux dependence \({\Gamma }_{\varphi \,{\mbox{E}}}^{\Phi }({\Phi }_{{{\rm{ext}}}})\) weakens as the magnetic field B∥ increases (cf. Fig. 2f), reminiscent of earlier observations in flux qubits at lower field38. We fit the flux noise amplitude \(\sqrt{{A}_{\Phi }}\) for a SΦ(ω) = AΦ/ω power spectral density using29,56.
$${\Gamma }_{\varphi \,{\mbox{E}}\,}^{\Phi }=\sqrt{{A}_{\Phi }\ln 2}\left\vert \frac{\partial \omega }{\partial {\Phi }_{{{\rm{ext}}}}}\right\vert \,.$$
(3)
With increasing B∥, we observe a decrease of \(\sqrt{{A}_{\Phi }}\) by a factor of ~2, reported in Fig. 2g, which holds across different qubit frequencies in several cooldowns (cf. Supplementary III). However, for B∥ ≳ 1 T, \(\sqrt{{A}_{\Phi }}\) increases, suggesting the onset of a competing mechanism, likely due to vortex dynamics in the magnet wires.
We model the flux noise as the sum of a large number of magnetic two-level fluctuators, consistent with the commonly accepted spin-based origin of flux noise57,58,59. Each of them constitutes a source of asymmetric random telegraphic noise, with a Lorentzian power spectrum \(S(\omega )\propto {({\Gamma }_{1}/{\Gamma }_{\uparrow }+{\Gamma }_{1}/{\Gamma }_{\downarrow })}^{-1}\cdot {\Gamma }_{1}/({\Gamma }_{1}^{2}+{\omega }^{2})\), where Γ1 = Γ↑ + Γ↓ are the excitation and relaxation rates of the fluctuator, respectively60. In the limit of identical fluctuators, S(ω) remains Lorentzian, while for fluctuators with 1/Γ1 uniformly distributed, S(ω) ∝ 1/ω56. However, for any distribution, the amplitude of the power spectrum is \({A}_{\Phi }\propto {({\Gamma }_{1}/{\Gamma }_{\uparrow }+{\Gamma }_{1}/{\Gamma }_{\downarrow })}^{-1}\), which becomes (cf. Supplementary III).
$${A}_{\Phi }\propto 1/{\cosh }^{2}\left(\frac{{\mu }_{{{\rm{B}}}}B}{{k}_{{{\rm{B}}}}{T}_{{{\rm{S}}}}}\right)\,.$$
(4)
Here, 2μBB is the energy of g = 2, s = 1/2 paramagnetic impurities and μB, kB and TS are the Bohr magneton, the Boltzmann constant and the spin bath temperature, respectively. A fit with TS = 85 mK aligns with the measured flux noise amplitude (black line in Fig. 2g) up to 1 T. This suggests the freezing of g = 2 paramagnetic impurities responsible for the reduction of flux noise, presumably the same spin environment that causes the T1 dip (cf. Fig. 2d).
In Fig. 3, we leverage the field resilience of the gralmonium to probe the magnetic susceptibility of a recently discovered TLS bath coupled to superconducting qubits34,47,55. These TLSs have been shown to induce non-Markovian qubit dynamics, and their long lifetime, exceeding 1/ΓTLS ≥50 ms, makes a spin-based origin plausible. Following ref. 34, by repeatedly preparing the qubit in either \(\left\vert \,{\mbox{g}}\,\right\rangle\) or \(\left\vert \,{\mbox{e}}\,\right\rangle\) using fast feedback over N = 104 iterations, the TLS ensemble hyperpolarizes via its cross-relaxation to the qubit. After this polarization sequence, the qubit is initialized in either \(\left\vert \,{\mbox{g}}\,\right\rangle\) or \(\left\vert \,{\mbox{e}}\,\right\rangle\), and its population is monitored using stroboscopic quantum jump measurements. Figure 3b shows the distinct signatures of a hyperpolarized long-lived TLS ensemble coupled to the gralmonium: regardless of the qubit’s initial state, it relaxes to the TLS ensemble population on a T1 timescale, while the TLS ensemble itself decays to thermal equilibrium on milliseconds timescale. By modeling the qubit coupled to a ladder of 102 TLSs34, we extract a gralmonium relaxation Γ1 = 1/5.4 μs, of which TLS cross-relaxation accounts for \({\sum }_{k}{\Gamma }_{\,{\mbox{qt}}\,}^{k}=1/22\,\mu {{\rm{s}}}\).
Fig. 3: Magnetic susceptibility of long-lived two-level-systems (TLSs) in high field.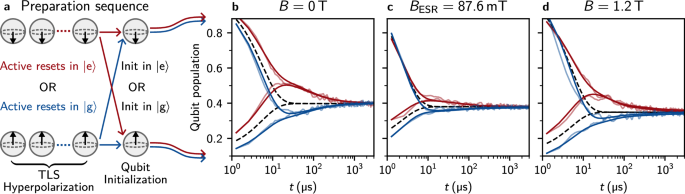
a Sketch of the qubit preparation sequence used in (b–d). The repeated (N = 104) active reset of the qubit state in \(\left\vert \,{\mbox{g}}\,\right\rangle\) or \(\left\vert \,{\mbox{e}}\,\right\rangle\) (blue and red traces in all panels, respectively) results in the hyperpolarization of environmental, long-lived TLS34. The last step of the preparation sequence consists in a qubit initialization in \(\left\vert \,{\mbox{g}}\,\right\rangle\) or \(\left\vert \,{\mbox{e}}\,\right\rangle\). We use a 540 ns rectangular readout pulse and a 32 ns Gaussian π-pulse. b Qubit population relaxation after the preparation sequence for different magnetic fields B∥. We fit the data (semi-transparent) to the theoretical model34,55 (opaque). For reference, the black dashed lines show an exponential decay with the qubit energy relaxation rate Γ1. In zero field, we reproduce the signatures of TLS hyperpolarization recently observed in other superconducting qubits34,35, i.e., undershoot (blue) and overshoot (red) compared to the single exponential decay. c At the ESR resonance field BESR, the hyperpolarization signatures are suppressed due to energy relaxation of the qubit into the paramagnetic ensemble. d The signatures of TLS hyperpolarization on qubit relaxation in magnetic fields exceeding 1 T are comparable to zero field, indicating a very low susceptibility of the long-lived TLSs to magnetic field.
In magnetic field, the signatures of TLS hyperpolarization remain visible, as illustrated in Fig. 3c, d. The fact that the hyperpolarization in B∥ = 1.2 T is comparable to zero field indicates that the TLS bath is not magnetically susceptible, ruling out origins, such as electronic spins. Remaining non-magnetically-susceptible microscopic origins include subgap states, possibly trapped quasiparticles61. As shown in Fig. 3c, at B ≈ BESR, where T1 is suppressed by a factor of 7 (cf. Fig. 2d), the TLS hyperpolarization is less pronounced. Therefore, we are still able to hyperpolarize the long-lived TLSs, but not the paramagnetic spins. This indicates that the spin ensemble is large enough or sufficiently coupled to the environment that it embodies a Markovian bath. In contrast, the long-lived TLS environment appears to be uncoupled to the spin ensemble, as evidenced by the fit in Fig. 3c with a practically unchanged cross-relaxation rate of \({\sum }_{k}{\Gamma }_{\,{\mbox{qt}}\,}^{k}=1/33\,\mu {{\rm{s}}}\).
In conclusion, we have introduced a field-resilient superconducting qubit—the gradiometric gralmonium—that operates robustly in Tesla magnetic fields. By incorporating a grAl nanojunction, the gralmonium maintains spectral stability and coherence in high magnetic fields, circumventing the Fraunhofer interference typically observed in JJ-based superconducting circuits. We reveal distinct properties of spin environments coupled to the gralmonium by addressing their magnetic field susceptibility. Using ESR, we characterize a paramagnetic spin-1/2 ensemble that couples transversely to the qubit, demonstrating the gralmonium’s potential as a probe for spin dynamics. We confirm the long-standing hypothesis of the freeze-out of fast flux noise in high fields, consistent with a spin s = 1/2, g = 2 paramagnetic origin. The operation of the gralmonium in magnetic field also allowed us to disprove the electron-spin hypothesis for the long-lived two-level system (TLS) environment responsible for non-Markovian qubit dynamics.
Future work should address flux noise suppression and spectral noise analysis, and should validate the correlation between flux noise and the spin-1/2 ensemble in order to gain insights into its microscopic origin. Most importantly, the gralmonium’s resilience to magnetic fields offers a promising path forward in hybrid quantum architectures, facilitating seamless integration with magnetic-field-sensitive systems, such as spins62, magnons, or topological materials.
