The quest to understand how networks achieve optimal performance under real-world limitations drives innovation across diverse fields, yet identifying the precise structures that maximise functionality remains a significant challenge. Guram Mikaberidze and Dane Taylor, from the School of Computing at the University of Wyoming, now present a new framework for discovering networks optimised for synchrony, a crucial property in systems ranging from power grids to advanced technologies. Their research reveals that these optimal networks possess surprising characteristics, being both sparse and highly organised in a way that defies conventional expectations. The team demonstrates that a carefully defined mathematical equation accurately predicts the best way to connect nodes, and a guiding principle governs how resources should be allocated within the network, ultimately leading to a system that achieves global coordination without a traditional synchronisation threshold.
Optimizing Synchronization in Complex Network Systems
Scientists are advancing our understanding of synchronization in complex networks, systems composed of interconnected oscillating units, with implications for diverse fields such as power grid stability and brain-inspired computing. This research focuses on maximizing synchronization, the coordinated behaviour of these oscillators, and achieving it efficiently within resource constraints. The work explores how network structure influences synchronization and develops algorithms to optimize network design for enhanced performance. A central concept is the Kuramoto model, a simplified representation of coupled oscillators that allows researchers to study the fundamental dynamics of synchronization.
Investigations reveal that small-world networks, possessing both local and long-range connections, can be particularly effective at promoting synchronized behaviour. However, the research also acknowledges the counterintuitive phenomenon of Braess’s paradox, where adding connections to a network can actually decrease overall performance, requiring careful consideration of network topology. Furthermore, scientists are exploring the use of nanoscale spintronic oscillators as building blocks for neuromorphic computing systems, leveraging synchronization to enable efficient information processing. By combining theoretical modelling, numerical simulations, and machine learning techniques, scientists are making significant strides towards improving the performance and reliability of critical infrastructure and unlocking the potential of brain-inspired computing.
Sparse Networks Maximise Synchrony with Limited Resources
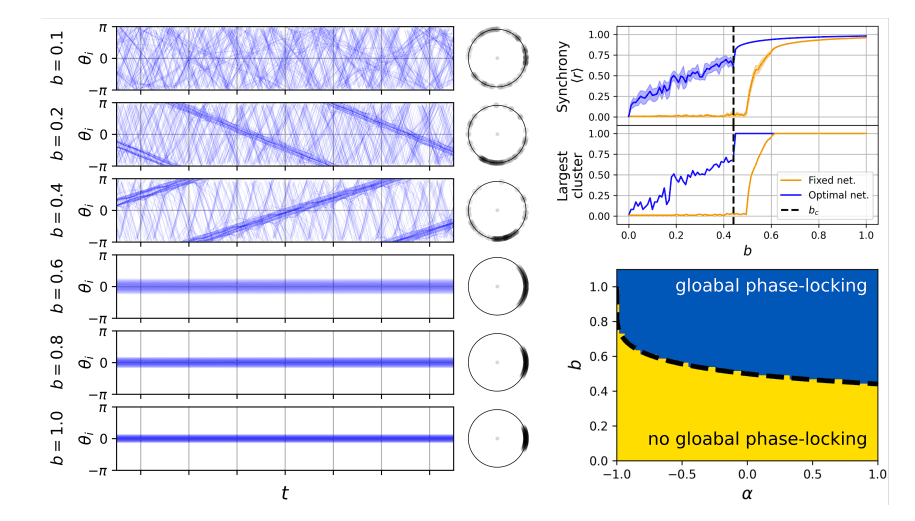
Scientists have discovered that remarkably sparse networks can achieve high levels of synchrony, the coordinated behaviour of interconnected oscillating units, while operating within strict resource constraints. This finding challenges conventional wisdom and offers a new approach to designing efficient and robust systems. The research employs a gradient-based optimization framework to identify network structures that maximize synchrony while adhering to a fixed coupling budget. Experiments reveal that optimal networks exhibit several counterintuitive features, including sparsity, bipartiteness, elongation, and monophily.
These networks are remarkably sparse, with most connections removed, and exhibit a bipartite structure, partitioning nodes based on their intrinsic frequency. Furthermore, the network structure elongates, forming long paths, and demonstrates strong monophily, where neighbours of any given node possess highly similar frequencies that differ from the node’s own. This consistent observation across multiple optimization runs suggests a fundamental role for these features in achieving optimal synchrony. The team also identified two distinct optimal network configurations, each recapitulating observations from prior network studies, and pinpointed the global optimum through rigorous analysis.
Measurements confirm that these optimized networks lack a traditional synchronization threshold, instead exhibiting global phase-locking as the coupling budget exceeds a calculable critical value. This research delivers an analytical prescription for optimally allocating node strengths, operating directly within the fully nonlinear Kuramoto regime, providing a predictive design principle for networks where synchronization is essential but resources are limited. This work reconciles previous anecdotal observations and offers practical guidance for designing high-performance networks in diverse applications, from power grids to neuromorphic computing.
Optimal Synchronisation With Limited Network Resources
Scientists have established a new understanding of how networks achieve optimal synchronisation under realistic constraints, moving beyond traditional models that assume unlimited resources. This research demonstrates that remarkably sparse networks, exhibiting a unique combination of features, can achieve high levels of synchronisation while operating within limited budgets. The team developed a gradient-based optimisation framework to identify network structures that maximise synchronisation while adhering to a fixed coupling budget. The resulting networks exhibit several counterintuitive features, including sparsity, a bipartite arrangement, elongation, and strong monophily, a tendency for nodes to connect with similar, yet distinct, partners.
Crucially, the team also constructed a corresponding theoretical framework, demonstrating that optimal network design can be described by a nonlinear differential equation governing edge placement and a variational principle dictating node strength allocation. This framework provides a powerful tool for understanding and predicting network behaviour. The findings demonstrate that synchronisation does not require a critical coupling strength, as previously thought, but instead emerges as soon as a calculable budget threshold is exceeded, leading to global phase-locking and predictable scaling behaviour. The resulting networks exhibit a universal architecture, independent of the specific coupling function, characterised by sparse, high-diameter, and bipartite connections. This work reconciles conflicting observations in the field and extends beyond oscillator systems, offering insights into phenomena like opinion dynamics and social network formation where similar efficiency principles may apply. While the research focuses on establishing these core principles, the authors acknowledge that the optimal edge weights are sensitive to the specific coupling functions and synchrony measures used, suggesting avenues for further investigation into the nuances of network design.