3D-rendering of quantum entanglement. (Image by Vink Fan on Shutterstock)
New mathematical breakthrough reveals entanglement follows universal laws across all dimensions, potentially advancing quantum error correction and fundamental physics.
In A Nutshell
Physicists derived a universal formula for Rényi entropy in conformal field theories, valid when the parameter n approaches zero.
The result applies to vacuum states with spherical entanglement regions and simplifies how quantum information spread is calculated.
A separate formula in 2D systems, derived using the “hot spot” method, holds for all values of n.
Though theoretical, this work may influence quantum computing, error correction, and models of spacetime.
FUKUOKA, Japan — Scientists studying the strange world of quantum physics have found something extraordinary. Within a specific family of quantum systems, information seems to entangle in a mathematically predictable way. The result is the first rigorous derivation of a universal formula describing this behavior, offering insight into one of quantum theory’s most puzzling phenomena: entanglement.
A team of theoretical physicists from Kyushu University, Caltech, and the University of Tokyo has published their findings in the journal Physical Review Letters. They provide a systematic and controlled derivation (rather than a discovery) of a previously conjectured formula describing how Rényi entropy behaves in conformal field theories (CFTs), a class of highly symmetric quantum systems.
Rényi entropy is a mathematical tool used to measure how much information is shared between two parts of a quantum system. When particles are entangled, knowing something about one instantly reveals information about the other, no matter how far apart they are. By focusing on how this information spreads, the researchers derived a precise formula that holds whenever the entangled region is shaped like a sphere, the system is in its lowest-energy (vacuum) state, and the parameter n approaches zero.
Quantum entanglement occurs when two particles are fully related to each other regardless of their distance. (Image by Ole.CNX on Shutterstock)
A Consistent Pattern in Quantum Information Sharing
Using advanced mathematical techniques, the researchers showed that in all CFTs, the amount of entanglement, measured as Rényi entropy, follows the same rule when the parameter n approaches zero. This might sound technical, but the implication is simple: in these specific quantum systems, information spreads in a predictable way, no matter the exact details of the particles involved.
This rule depends only on the shape of the boundary between entangled regions and a constant related to the theory’s energy properties. It’s a bit like discovering that no matter the ingredients, baking a cake always follows the same temperature-to-time ratio if you’re using a spherical pan and starting with cold batter.
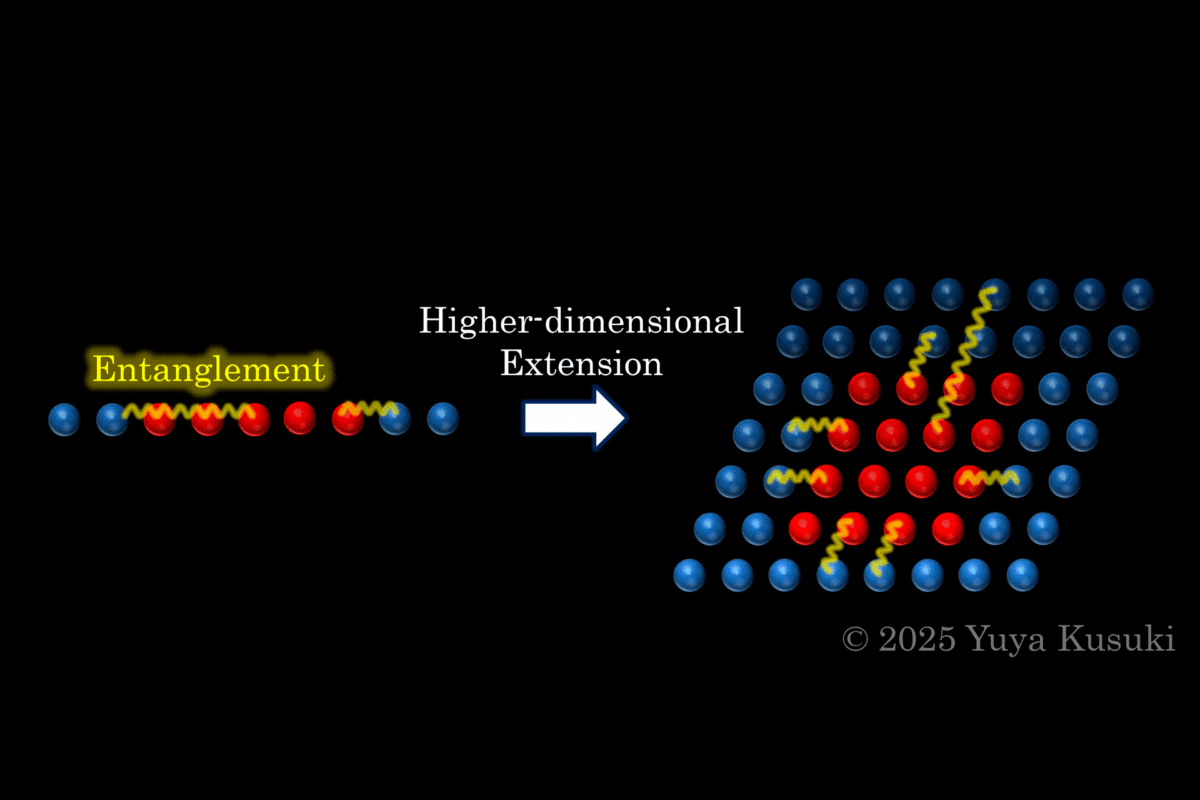
Quantum entanglement in 1+1 and 2+1 dimensions. (Credit: Yuya Kusuki)
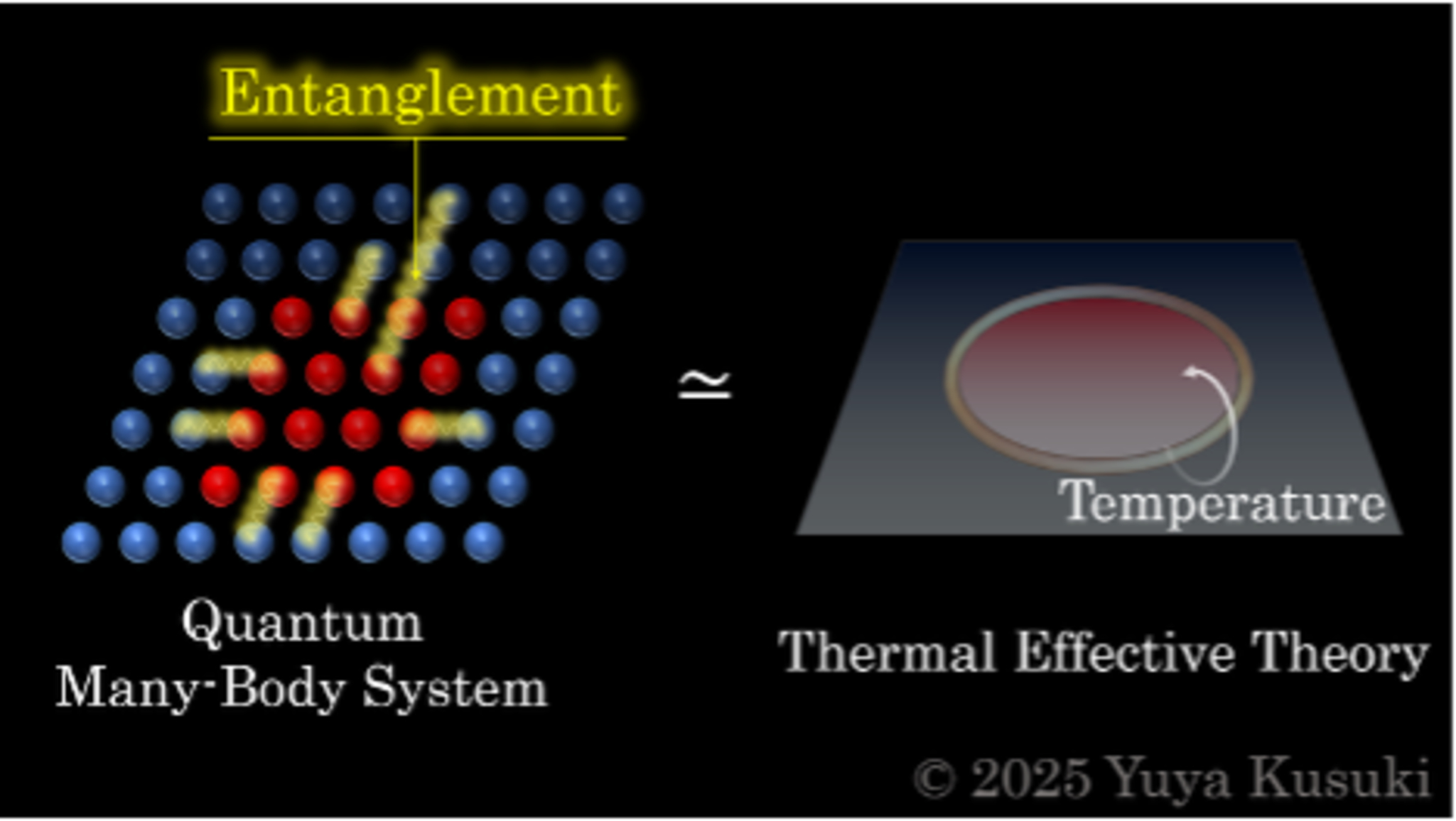
How They Did It: The Power of Thermal Thinking
To uncover this pattern, the team used what’s called “thermal effective theory,” a method that treats quantum systems as if they have a kind of temperature, even when they’re not physically hot. This trick lets physicists simplify otherwise impossible calculations by focusing on the system’s big-picture behavior rather than tracking every individual particle.
In doing so, they also revealed how the system’s entanglement spectrum, (essentially, how information is distributed across different energy levels) matches what one would expect from other areas of quantum theory. Their result wasn’t just elegant; it was consistent with known physics.
Interestingly, the paper shows that two-dimensional systems behave differently from those in higher dimensions. In 2D, a separate formula derived using a method known as the “hot spot idea” applies to all values of the parameter n. However, the universal formula presented in this work holds only in the n approaching zero limit.
In higher dimensions, the hot spot technique is not directly applicable due to how temperature-like effects behave near the boundary of entangled regions. These effects become more complex and prevent a straightforward generalization of the 2D result.
“This study is the first example of applying thermal effective theory to quantum information,” said lead author Yuya Kusuki, an associate professor at the Kyushu University Institute for Advanced Study, in a statement. “The results of this study demonstrate the usefulness of this approach, and we hope to further develop this approach to gain a deeper understanding of quantum entanglement structures.”
Implications for Quantum Computing and Beyond
Although the study is theoretical, it could have real-world relevance down the line. Quantum computers rely on entangled particles to perform calculations that ordinary computers can’t. Knowing exactly how entanglement behaves could help engineers build more reliable machines and develop better error correction methods.
The researchers’ methods may also help in understanding the fabric of spacetime itself. Some cutting-edge theories suggest space and time might emerge from patterns of quantum entanglement. If true, this new derivation could be a small but crucial piece of that cosmic puzzle.
“The boundary thermal effective theory developed here is highly versatile,” the authors write, suggesting that their approach could be applied to other systems in future research.
Disclaimer: This article summarizes findings from a theoretical physics study. The results apply to a specific class of mathematical models (conformal field theories) under controlled conditions and do not reflect experimental evidence. Any mention of practical applications—such as quantum computing or spacetime modeling—is speculative and should be interpreted accordingly.
Paper Summary
Methodology
The researchers used thermal effective theory to analyze Rényi entropy in conformal field theories. Focusing on spherical entanglement regions in vacuum states, they worked in the mathematical limit where the parameter n approaches zero. This allowed them to derive a universal formula that simplifies calculations by treating quantum systems as if they behave like hot gases.
Results
The study proved that Rényi entropy follows a predictable, universal formula under specific conditions in the n approaching zero limit. This formula depends only on the boundary area of the entangled region and not on the details of the quantum system. In two dimensions, a separate formula derived using the hot spot method applies for all values of n.
Limitations
The universal formula was proven only for spherical entangling regions and only in the limit where n approaches zero. While the authors conjecture that similar formulas may apply to more general shapes, this has not been proven. The hot spot idea, useful in 2D, is not directly applicable in higher dimensions due to boundary complications.
Funding and Disclosures
The research was supported by multiple sources, including the U.S. Department of Energy Office of Science, the Walter Burke Institute for Theoretical Physics at Caltech, the Simons Investigator grant, JSPS Grants-in-Aid for Scientific Research, the INAMORI Frontier Program at Kyushu University, the Kavli Institute for Theoretical Physics, and the Aspen Center for Physics.
Publication Details
Title: Universality of Rényi Entropy in Conformal Field Theory
Authors: Yuya Kusuki, Hirosi Ooguri, Sridip Pal
Journal: Physical Review Letters, Vol. 135, August 5, 2025
DOI: 10.1103/fsg7-bs7q