Observing the dynamics of quantum states generated inside nonlinear optical cavities

Experimental setup

Here, we briefly introduce our experimental setup. More detailed description of the setup can be found in the Supplementary Note 4.

Laser

For the laser system, a Toptica FemtoFiber ultra 780 was customized to provide dual-wavelength femtosecond pulses, with 780 nm and 1560 nm. A total of 780 nm signal is used to pump the OPO, and 1560 nm signal is split into two different lines, one is the bias field and the other is the local oscillator (LO) that is used to measure the phase of the OPO steady-state. Pump and bias field have the same polarization state, and they are orthogonal to the polarization of the LO signal.

OPO

The OPO consists of a MgO:PPLN crystal (MSHG1550-0.5-1, Covesion Ltd., United Kingdom) in a free-space bow tie optical cavity. The crystal is placed on the oven mount (PV10, Covesion Ltd., United Kingdom), which is connected to the temperature controller (OC2, Covesion Ltd., United Kingdom). The cavity length is matched to a single round trip of the laser pulse, and stabilized by detecting the power of the out-coupled sum-frequency mixed signal between the pump and the OPO signal40. The out-coupled sum-frequency mixed signal passes a narrow-band pass filter, which gives a linear change in the detected signal power as the cavity length deviates from the degenerate mode. A photodetector measures this error signal and a proportional-integral-derivative controller yields a voltage feedback to the piezoelectric actuator (PA44M3KW, Thorlabs, USA) attached to one of the cavity mirrors. To collect the statistics of the OPO steady-state and measure the probability, we modulate the pump and the bias signal at 10 kHz using a lithium niobate electro-optic modulators (EO-AM-NR-C1, EO-AM-NR-C3, Thorlabs, USA for amplitude modulation, and EO-PM-NR-C1, EO-PM-NR-C3, Thorlabs, USA for phase modulation). The cavity lifetime is calculated from the loss of the OPO signal from each cavity mirror, which gives  ~300 ns.

Preparing bias signal

To match the temporal alignment between pump and bias pulses, we use an optical delay line with a linear translational stage. Additional precision could be achieved by using an electronically controlled motorized actuator (PIA25, Thorlabs, USA). To attenuate the bias signal before entering to the cavity, the bias field first passes a series of neutral density filters (NDC-100S-4, Thorlabs, USA). Then we use a combination of waveplates and polarizers to further attenuate the bias field. The last waveplate is mounted on a motorized precision rotation stage (KPRM1E/M, Thorlabs, USA) which can be electronically controlled.

Measuring bias field

Because the bias pulse entering the cavity contains less than a few photons, we use the following protocol to measure the amplitude of the bias field. First, we place the power meter after the last polarizer and set the waveplate angle that gives the maximum bias power P0. Then the bias power at waveplate angle ϕ would be written as \(P={P}_{0}{\cos }^{2}(2(\phi -{\phi }_{0}))\), where ϕ0 is the angle that gives the maximum power. We rotate the angle of the waveplate to sweep the bias field and measure the bias–probability curve. After passing the last polarizer, we calculate the actual bias power that interacts inside the crystal, considering all the possible power loss happening at each optical component before it reaches at the crystal. The loss of each element is obtained either from our previous measurements25 or the manufacturer. Then we calculate the bias field \(b=\frac{{E}_{{{{{\rm{bias,mean}}}}}}}{{T}_{{{{{\rm{rt}}}}}}}\sqrt{\frac{\epsilon V}{\hslash {\omega }_{0}}}\). Ebias,mean is the mean electric field of the bias, Trt is the round trip time of the cavity, ϵ is the electric permittivity of the MgO:PPLN crystal, V is the mode volume, and ω0 is the angular frequency of the bias field. We use pulse duration of 190 ns, beam waist of 10 μm to calculate Ebias,mean and V25.

Although we initially estimated the bias field by measuring the power loss at each optical element, more precise calibration of the bias field can be achieved by measuring the bias–probability relationship of the quantum vacuum state. Details of the calibration method can be found in the Supplementary Note 4.

Measuring the statistics of the OPO steady-states

The sampled OPO signal and the LO are combined in a standard interferometry setup to measure the phase of the OPO steady-state. The polarization states of the OPO signal and the LO are matched before they are combined with the beam splitter cube. We add an additional delay stage on the LO line, using the same module that we used to control the temporal alignment between the pump and the bias pulses. Using the one output arm of the beam splitter, we check the temporal alignment between the OPO signal and the LO by observing the inference pattern with the camera (CMLN-13S2M-CS, Edmund Optics, USA). For the other arm, we measure the interference pattern with the photodetector (PDA50B2, Thorlabs, USA). The detected signal was recorded on the oscilloscope, collecting either 1000 (Fig. 2) or 10,000 OPO steady-states (Fig. 3) to measure the probability at a given bias field. The probability is defined as the number of steady-states with phase 0 rad divided by the number of total steady-states measured with the oscilloscope41.

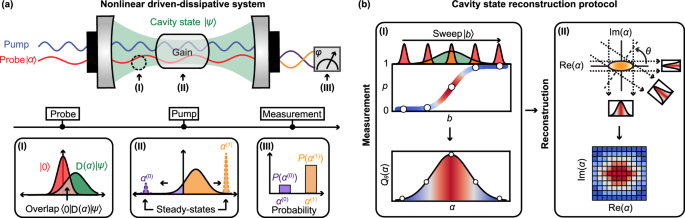
Reconstruction protocol

In this section, we describe some mathematical background on our Husimi Q function reconstruction protocol by measuring the sensitivity of the bias–probability relationship.

Husimi Q function

The Husimi Q function gives the probability of observing a certain coherent state \(\left\vert \alpha \right\rangle\) for a given quantum state \(\left\vert \psi \right\rangle\):

$$Q(\alpha,{\alpha }^{*}) =\frac{1}{\pi }\left\langle \alpha | \rho | \alpha \right\rangle \\ =\frac{1}{\pi }| \left\langle \alpha | \psi \right\rangle {| }^{2}.$$

(2)

The Husimi Q function can be either reconstructed with a standard homodyne detection setup that combines the unknown quantum state \(\left\vert \psi \right\rangle\) with a reference coherent state \(\left\vert \alpha \right\rangle\)42 or directly measured by using a heterodyne setup43, which is also known as a double homodyne setup. We rewrite Eq. (2) using the displacement operator D(α):

$$Q(\alpha,{\alpha }^{*}) \equiv \frac{1}{\pi }| \left\langle \alpha | \psi \right\rangle {| }^{2}\\ =\frac{1}{\pi }| \left\langle 0| D(-\alpha )| \psi \right\rangle {| }^{2}.$$

(3)

Equation (3) shows that measuring the Husimi Q function is equivalent to measuring the overlap between the displaced quantum state \(D(-\alpha )\left\vert \psi \right\rangle\) and quantum vacuum state \(\left\vert 0\right\rangle\).

Displacement operator

The stochastic differential equation of the OPO signal defined along the real quadrature of the phase space X can be written as below25:

$$\dot{X}=(\lambda -1)X+\sqrt{2}b+\sqrt{\lambda }{\eta }_{X}.$$

(4)

Here, ηX is the Gaussian noise. Because the derivative of the drift term \((\lambda -1)X+\sqrt{2}b\) with respect to X is positive when the OPO is pumped above threshold (i.e., λ > 1), the sign of the drift term at the time when the bias field is injected determines whether X will grow exponentially toward positive or negative side. Therefore, the direction of the amplification can be determined by the sign of the drift term. The critical point X0 with zero drift happens at \({X}_{0}=-\sqrt{2}b/(\lambda -1)\). X0 = 0 for an unbiased OPO, meaning that the amplification behavior of the cavity quantum state \(\left\vert \psi \right\rangle\) in the biased OPO is identical to that of displaced quantum state \(D(b)\left\vert \psi \right\rangle\) in the unbiased OPO, where the displacement operator D(b) defined along the X quadrature is written as:

$$D(b)\equiv \frac{\sqrt{2}b}{\lambda -1}.$$

(5)

Reconstructing marginal distribution of the Husimi Q function

After the bias field displaces the quantum state, the OPO signal is amplified until it reaches one of the steady-states. As we described in the previous section, the original quantum state \(\left\vert \psi \right\rangle\) in the biased OPO shows the same dynamics as \(D(b)\left\vert \psi \right\rangle\) in the unbiased OPO system. The parametric amplification process is phase-sensitive, so X > 0 (or equivalently Re(α) > 0) part of the displaced quantum state gives the probability p of measuring a certain steady-state, which can be analytically described as:

$$p(b| \theta )\equiv \int_{\alpha=0}^{\alpha=\infty }| {\psi }_{\theta,D(b)}(\alpha ){| }^{2}d\alpha,$$

(6)

where \(\left\vert {\psi }_{\theta,D(b)}\right\rangle \equiv D(b)\left\vert {\psi }_{\theta }\right\rangle\). Because the phase-sensitive amplification happens along one quadrature, we consider the marginal distribution \(\left\vert {\psi }_{\theta }\right\rangle\). Using basic algebra,

$$p(b| \theta ) \equiv \int_{-D(b)}^{\infty }| {\psi }_{\theta }(\alpha ){| }^{2}d\alpha \\ ={\left\langle {\psi }_{\theta }| {\psi }_{\theta }\right\rangle }_{[-D(b),\infty ]}\\ ={\left\langle {\psi }_{\theta }| I| {\psi }_{\theta }\right\rangle }_{[-D(b),\infty ]}\\ =\frac{1}{\pi }\int| \left\langle {\psi }_{\theta }| \alpha \right\rangle {| }_{[-D(b),\infty ]}^{2}\,{d}^{2}\alpha \\ =\int_{-D(b)}^{\infty }\int_{-\infty }^{\infty }Q\,\,{\mbox{dIm}}({\alpha }_{\theta }){\mbox{dRe}}\,({\alpha }_{\theta }).$$

(7)

We introduced the identity operator \(I=\frac{1}{\pi }\int\left\vert \alpha \right\rangle \left\langle \alpha \right\vert {{\mbox{d}}}^{2}\alpha\), to expand the representation from a specific coordinate to the 2D phase space. The final expression represents the same probability but now sums over the possible coherent states in the region of interest. Therefore, by taking the derivative with respect to D(b), we can reconstruct the marginal distribution Qθ.

Stochastic differential equations

Until now, we have focused on using the displacement operator to understand how the bias field b affects the probability p. In this section, we provide another approach, which solves the SDE of the OPO system to calculate the bias–probability relationship. When a time-dependent bias field b(τ) is introduced, the OPO dynamics at the linear amplification stage can be written as:

$$\dot{X}=(\lambda -1)X+\sqrt{2}b(\tau )+\sqrt{\lambda }{\eta }_{X}.$$

(8)

With Z = Xe−(λ−1)τ,

$$Z(\tau )=Z(0)+\int_{0}^{\tau }{e}^{-(\lambda -1)\tau {\prime} }[\sqrt{2}b(\tau {\prime} )+\sqrt{\lambda }{\eta }_{X}(\tau {\prime} )]d\tau {\prime} .$$

(9)

Calculating the positive area of the probability distribution of Z(τ), we can calculate the probability p. When a constant bias field b0 is injected at τ = τ0,

$$P[Z(\tau )\ge 0]=P\left[f(\tau )\ge -\frac{\sqrt{2}{b}_{0}}{\sqrt{\lambda }}\frac{{e}^{-(\lambda -1){\tau }_{0}}-{e}^{-(\lambda -1)\tau }}{\lambda -1}\right],$$

(10)

$$f(\tau )\equiv \int_{0}^{\tau }{e}^{-(\lambda -1)\tau {\prime} }{\eta }_{X}(\tau {\prime} )d\tau {\prime}$$

(11)

Because X(τ) is the Wiener process (linear superposition of Gaussian noises), f(τ) is a Gaussian with mean 〈f(τ)〉 = 0, and variance \(\langle \,{f}^{2}(\tau )\rangle=\frac{1-{e}^{-2(\lambda -1)\tau }}{2(\lambda -1)}\). Therefore,

$$P[Z(\tau )\ge 0]=\int_{-{f}_{0}(\tau )}^{\infty }\frac{1}{\sqrt{2\pi \langle \,{f}^{2}(\tau )\rangle }}{e}^{-\frac{{f}^{2}}{2\langle \,{f}^{2}(\tau )\rangle }}df,$$

(12)

where \({f}_{0}(\tau )\equiv \frac{\sqrt{2}{b}_{0}}{\sqrt{\lambda }}\frac{{e}^{-(\lambda -1){\tau }_{0}}-{e}^{-(\lambda -1)\tau }}{\lambda -1}\). As we measure the probability p after several cavity cycles, which corresponds to the time τ when e−(λ−1)τ → 0+, so the probability p becomes

$$p\equiv P[Z(\tau )\ge 0]=\frac{1}{2}\left(1+\,{\mbox{erf}}\,\left[\frac{\sqrt{2}{b}_{0}{e}^{-(\lambda -1){\tau }_{0}}}{\sqrt{\lambda }\sqrt{\lambda -1}}\right]\right),$$

(13)

where erf is the Gauss error function. In the Supplementary Information 3 and 5, we discuss the SDEs for time-dependent λ(τ) and b(τ).