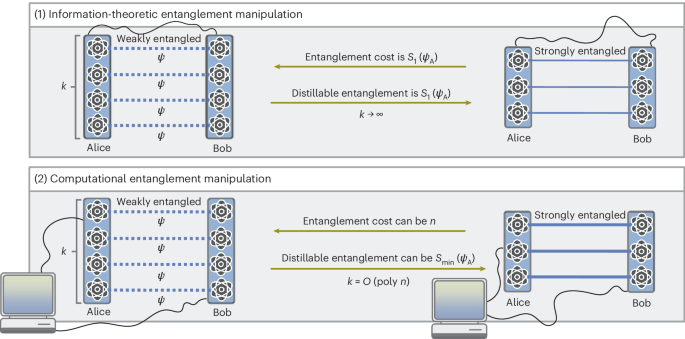
We now aim to determine the fundamental limits and possibilities of computationally efficient entanglement manipulation. Here the goal is to precisely characterize the computational distillable entanglement and the computational entanglement cost by establishing bounds on the optimal rates and providing LOCC protocols that achieve them.
However, when revisiting entanglement theory through a computational lens, another crucial aspect becomes evident: the optimal conversion rates that we introduced in Definitions 1 and 2 implicitly assume that Alice and Bob have perfect knowledge of the state. While the mere existence of a computationally efficient protocol may provide achievability bounds on computational entanglement measures, this assumption contradicts the perspective adopted in this work. Having perfect knowledge of the state means fully characterizing it, but given the exponential growth of the Hilbert space dimension with the number of qubits n, this lies fundamentally beyond the realm of computational feasibility. For entanglement manipulation tasks to remain meaningful in a computationally constrained scenario, there are essentially two possibilities.
(1)
State agnostic: Alice and Bob are given (at most polynomially many) copies of an unknown quantum state, with the goal of manipulating and characterizing its entanglement.
(2)
State aware: Alice and Bob possess an efficient classical description of the state, which they use to manipulate and characterize its entanglement.
For what concerns efficient entanglement distillation, the state-agnostic scenario limits Alice and Bob to gather information on the unknown state \(| {\psi }_{\rm{AB}}\left.\right\rangle\) through efficient local measurements on O(poly n) samples, which inform their LOCC distillation protocol but reduce the distillation rate owing to measurement-induced consumption of copies. In the state-aware scenario, instead, they have full circuit-level knowledge of the state but may still face the computational intractability of extracting key properties like the Schmidt eigenbasis and coefficients, crucial for optimal LOCC design.
For entanglement dilution, the settings are analogous. In the state-agnostic case, Alice and Bob have local access to O(poly n) copies of an unknown bipartite state and use measurements to inform an LOCC protocol that minimizes ebits consumption. Unlike distillation, measured (local) copies here do not count against resources. In the state-aware case, they additionally have the state’s classical description and aim to design an efficient LOCC protocol based on this information.
Having cleared the framework of entanglement manipulation in the computationally constrained regime, we now quantify the limits and capabilities of the state-agnostic and state-aware scenarios, starting with the former. Surprisingly, our analysis reveals a deep connection between the two: in the worst case, state-awareness offers no advantage, as the fully state-agnostic approach is fundamentally optimal.
State-agnostic scenario
We begin our investigation of the state-agnostic setting by first considering entanglement distillation. We note that previous works have already highlighted some limitations in the computationally constrained setting. Specifically, the discovery of pseudoentangled quantum states22 reveals computationally indistinguishable families of bipartite pure states with an entanglement gap of Ω(n) versus O(polylog n), establishing that no state-agnostic protocol can distil more than \(O(\log n)\) ebits in the worst case. Our work goes beyond this result, showing that this bound is overly optimistic and cannot be achieved by any state-agnostic protocol in many scenarios. Furthermore, we show that our worst-case bounds are actually achievable, by providing an explicit state-agnostic and computationally efficient distillation protocol (‘Theorem 2’).
The crux of our no-go results is the construction of families of statistically indistinguishable pseudoentangled states with a maximal entanglement gap of \(\tilde{\varOmega }(n)\) versus o(1) (equation (1)) across a fixed extensive bipartition A∣B. This has a profound implication: state-agnostic protocols with limited sample complexity cannot distil any ebits from general quantum states, even when the von Neumann entropy is maximal, which thus strengthens existing bounds on the limitations of such protocols. At the same time, these pseudoentangled families exhibit o(1) entanglement when quantified by the min-entropy \({S}_{\min }\). This suggests that the min-entropy is a key quantity determining the fundamental limitations of distillation protocols in computationally constrained, state-agnostic scenarios. Building on this, we refine our construction to create pseudoentangled families with tunable min-entropy \({S}_{\min }\), leading to the formulation of our main state-agnostic no-go result.
Theorem 1
(No-go on state-agnostic distillation: informal). Any sample-efficient and state-agnostic approximate LOCC distillation protocol cannot distil more than \(\min \{{S}_{\min }({\psi }_{\rm{A}})\,+\,o(1),2\log k\,+\,O(1)\}\) ebits from k copies of a bipartite input state \(| {\psi }_{AB}\left.\right\rangle\), regardless the value of the von Neumann entropy S1(ψA).
Proof
The proof reduces to the construction of two statistically indistinguishable families of states with the same min-entropy \({S}_{\min }\) and a tunable von Neumann entropy gap, which can be maximal (\(\tilde{\varOmega }(n)\) versus \(O({S}_{\min })\)). The construction is relatively straightforward as it considers states of the form
$$\begin{array}{rcl}| {\varPsi }_{\rm{AB}}\left.\right\rangle &=&\sqrt{1-\eta }{| 0\left.\right\rangle }_{\rm{A}}{| 0\left.\right\rangle }_{\rm{B}}{| 0\left.\right\rangle }^{\otimes n-2{S}_{\min }}{| {\phi }_{\rm{AB}}^{+}\left.\right\rangle }^{\otimes {S}_{\min }}\\ &&+\sqrt{\eta }{| 1\left.\right\rangle }_{\rm{A}}{| 1\left.\right\rangle }_{\rm{B}}| {\psi }_{\rm{AB}}\left.\right\rangle ,\end{array}$$
(1)
where \(| {\psi }_{\rm{AB}}\left.\right\rangle\) may encode either a Haar random state or a suitable pseudoentangled quantum state, which, in our case, is chosen to be obtained by means of a classical bit-string permutation applied to a smaller Haar subsystem. The parameter η ∈ [0, 1] is appropriately chosen to tune the entanglement gap. Since the two families of states are statistically indistinguishable and have a tunable entanglement gap, any state-agnostic distillation rate cannot exceed the lowest value of S1 among the two, which coincides with \({S}_{\min }\) or \(\log k\) for appropriate choices of the pseudoentangled families. For the complete rigorous proof, we refer to Supplementary Information Section B.3.
Somewhat unexpectedly, even in the regime of low entanglement \({S}_{1}=O(\log n)\), the von Neumann entropy is completely inaccessible to any sample-efficient state-agnostic protocol and the distillable entanglement is instead captured by the min-entropy. In the particular case where \({S}_{\min }=\varOmega (\,\text{polylog}\,n)\) we recover, as a special case, the results of ref. 22, as the bound in Theorem 1 simplifies to \(O(\log k)\), which coincides with \(O(\log n)\) when poly n input copies are available.
Now a crucial question becomes evident: does an efficient state-agnostic protocol exist that achieves the limitations imposed by Theorem 1? We hereby provide a positive answer by presenting a finite-shot regime analysis of a protocol originally considered in the asymptotic setting in ref. 37. This protocol is state agnostic and relies on the Schur transform, which leverages permutation symmetry to decompose a k-fold tensor product state onto irreducible subspaces of the symmetric and unitary groups38. Crucially, this decomposition features maximally entangled states in orthogonal (irreducible) subspaces, which can thus be extracted by means of local operations without perturbation. Remarkably, the Schur transform can be implemented efficiently on a quantum computer when k = O(poly n) (refs. 39,40). Although the complete description of the distillation protocol requires several technical preliminaries and is deferred to Supplementary Information Sections A.5 and B.1, here we present the main takeaway result in the following informal theorem.
Theorem 2
(State-agnostic distillation performance: informal). There exists an explicit, state-agnostic and computationally efficient distillation protocol that approximately distils at a rate \(\min \{\varOmega ({S}_{\min }({\psi }_{\rm{A}})),\varOmega (\log k)\}\) from poly-many copies of any given input state \(| {\psi }_{\rm{AB}}\left.\right\rangle\). In other words, for any state,
$${\hat{E}}_{\rm{D}}^{(k)}({\psi }_{\rm{AB}})\ge \min \{\varOmega ({S}_{\min }({\psi }_{\rm{A}})),\varOmega (\log k)\}.$$
(2)
Taken together, Theorems 1 and 2 establish achievable and optimal (up to logarithmic factors) rates for state-agnostic entanglement distillation when given access to k = O(poly n) copies of the input state. Furthermore, since the optimal protocol is computationally efficient, its optimality holds even under (more strict) computational constraints. These results provide a definitive benchmark for what is achievable in the state-agnostic and sample-efficient regime, shedding light on its fundamental limitations and possibilities. We note that, when \(k=\varOmega (\exp n)\), the protocol considered in Theorem 2 achieves the von Neumann entropy rate37; therefore state-agnostic protocols are essentially information-theoretically optimal when the sample-complexity scales exponentially.
Clearly, the no-go result in Theorem 1 leaves open the existence of agnostic protocols that may achieve higher rates on some restricted classes of states. For example, as we show in Supplementary Information Section C.2, this is the case for low-rank states, for which the protocol analysed in Theorem 2 distils at the (information-theoretically maximal) von Neumann entropy rate. Notably, these states may not be efficiently simulable. This reveals a gap between the simulability of quantum states and the efficient manipulation of their entanglement. This has already been noted in ref. 41, where optimal and computationally efficient entanglement manipulation of entanglement-dominated t-doped stabilizer states has been shown beyond the classical simulability barrier.
Because the results in Theorems 1 and 2 cover only the state-agnostic scenario, an immediate question is: are there states for which the state-agnostic rate above is optimal among all computationally efficient protocols? Surprisingly, the answer is positive, as stated by the following theorem.
Theorem 3
(Tight upper bound on computational distillable entanglement: informal). Let n be sufficiently large. Then there exists at least one state \(| {\psi }_{\rm{AB}}^{* }\left.\right\rangle\) with von Neumann entropy \(\tilde{\varOmega }(n)\) and computational distillable entanglement \({\hat{E}}_{\rm{D}}^{(k)}({\psi }_{\rm{AB}}^{* })\le \min \{{S}_{\min }({\psi }_{\rm{A}}^{* }),\log k\}+o(1)\), for any k = O(poly n).
Proof
The proof relies on the key fact that the pseudoentangled state families in equation (1), although not being pseudorandom, exhibit strong pseudorandom components. This leads to a concentration of measure phenomena, ensuring that any LOCC operation acting on the highly entangled ensemble as defined by equation (1) yields results close to the respective Haar average. Because computationally efficient LOCCs are ‘only’ 2O(poly n) in number, although the concentration is doubly exponential, on most states any efficient LOCC must produce an output concentrating near the average. Finally, as the Haar average is statistically close to the pseudorandom one and the two families have a tunable entanglement gap, the distillation rate is upper bounded by the family with the lowest entanglement content, as quantified by the von Neumann entropy. See Supplementary Information Section B.4 for a detailed proof.
Together, Theorems 2 and 3 provide a complete worst-case characterization of the computational distillable entanglement. Notably, they demonstrate that there exist states for which the computational distillable entanglement precisely satisfies
$${\hat{E}}_{\rm{D}}^{(k)}=\min \{\varTheta ({S}_{\min }),\varTheta (\log k)\},$$
(3)
regardless the value of the von Neumann entropy S1. This result reveals that in a computationally constrained setting, the min-entropy takes on a pivotal role, replacing the von Neumann entropy as the key quantity traditionally associated with asymptotic entanglement distillation. Moreover, it reaffirms the optimality of the state-agnostic protocol discussed in Theorem 2.
We now turn to describing our results for the converse task: state-agnostic entanglement dilution. Here, the simplest state-agnostic dilution procedure is the quantum teleportation protocol8, which, starting from local copies of the state to be diluted, consumes n ebits per copy to distribute the state non-locally across the bipartition A∣B. Although quantum teleportation seems highly inefficient in terms of the consumed entanglement, our construction of pseudoentangled states (equation (1)) implies that quantum teleportation is, in fact, optimal in terms of ebits consumption, even when the von Neumann entropy is o(1). This is summarized in the following theorem.
Theorem 4
(No-go on state-agnostic entanglement dilution: informal). Any sample-efficient, state-agnostic and approximate dilution protocol cannot dilute at a rate less than \(\tilde{\varOmega }(n)\), irrespective of the value of the von Neumann entropy, which can be o(1).
This establishes that quantum teleportation, being state-agnostic and computationally efficient, is worst-case optimal among all other agnostic protocols in terms of ebits consumption even for states with vanishingly small entanglement, that is, S1 = o(1).
Similarly to the case of entanglement dilution, one might ask whether there exist states for which quantum teleportation remains the optimal computationally feasible approach to entanglement dilution when compared with arbitrary computationally efficient protocols. In the following theorem, we address this question by demonstrating the existence of states with a computational entanglement cost lower bounded by \(\tilde{\varOmega }(n)\), regardless of their von Neumann entropy.
Theorem 5
(Tight lower bound on computational entanglement cost:informal). Let n be sufficiently large. Then there exists at least one state \(| {\psi }_{\rm{AB}}^{* }\left.\right\rangle\) with computational entanglement cost \({\hat{E}}_{\rm{C}}^{(k)}({\psi }_{\rm{A}}^{* })\ge \tilde{\varOmega }(n)\), irrespective of the (arbitrarily small) value of the von Neumann entropy \({S}_{1}({\psi }_{\rm{A}}^{* })\).
As a direct consequence of Theorem 5 and of quantum teleportation, we achieve a full worst-case characterization of the computational entanglement cost. Specifically, we show the existence of states for which \({\hat{E}}_{\rm{C}}^{(k)}=\tilde{\varTheta }(n)\), despite having an arbitrarily low information-theoretic entanglement cost, as quantified by the von Neumann entropy.
As a corollary of Theorem 5, the same worst-case bounds apply to the task of state compression31, where Alice aims to compress many i.i.d. copies of a mixed quantum source ρA to minimize the uses of a noiseless quantum channel for transmitting the source to Bob. Asymptotically, the optimal compression rate is again given by S1(ρA) (ref. 31). Because state compression can serve as a dilution protocol—with Alice first encoding the state and then teleporting its compressed version—the no-go result of Theorem 5 (as well as any other no-go on the entanglement cost) applies directly (for more details, see Supplementary Information Section D).
State-aware scenario
Having examined the state-agnostic scenario, we now consider the state-aware setting, where the agents have an efficient classical description of the state they wish to manipulate. However, as we anticipated, this knowledge does not grant efficient access to the optimal state conversion protocol, as computing key figures of merit may remain computationally unfeasible. The next theorem formalizes this intuition, showing that even with a classical description, designing a better-performing LOCC protocol than in the state-agnostic case remains computationally intractable in the worst case. This result holds under the assumption that the LWE decision problem is computationally hard to solve for a quantum computer (Supplementary Information Section A.6), which is a widely adopted assumption in post-quantum cryptography32.
Theorem 6
(No-go on state-aware entanglement manipulation: informal). Let δ > 0. Assuming that the LWE problem is superpolynomially hard to solve on a quantum computer, the following two statements hold.
(1)
No computationally efficient protocol can be efficiently designed to distil at a rate larger than \({S}_{\min }({\psi }_{\rm{A}})+o(1)\) from k copies of a bipartite pure quantum state \(| {\psi }_{\rm{AB}}\left.\right\rangle\), even when provided with an efficient circuit description of the state. This limitation holds regardless of the value of \({S}_{1}({\psi }_{\rm{A}})\,=\,\tilde{O}({n}^{1-\delta })\) and for \({S}_{\min }({\psi }_{\rm{A}})\,=\,O({n}^{\delta })\).
(2)
any computationally efficient protocol efficiently designed to dilute k copies of a bipartite state starting from its efficient circuit description must consume more than Ω(n1 − δ) ebits. This result holds regardless of the value of S1(ψA) = O(n1 − δ).
This reveals a surprising insight: although the state-aware scenario seems advantageous, it does not necessarily improve conversion rates over the fully state-agnostic case. For certain state classes, the information needed to design superior LOCC protocols remains computationally inaccessible, even with a classical description.
Notably, Theorem 6 does not rule out the existence of efficient LOCC protocols for entanglement manipulation. Unlike Theorem 3 and Theorem 5, it imposes no bounds on computational entanglement measures but prevents Alice and Bob from efficiently identifying such a protocol.
Despite its worst-case limitations, Theorem 6 does not preclude improvements in some specific scenarios. For example, ref. 41 shows that for t-doped stabilizer states with sufficiently high entanglement, knowing the associated stabilizer group enables computationally efficient distillation and dilution at the von Neumann entropy rate.