Effective descriptions of bosonic systems can be considered complete

Bosonic quantum information theory

Quantum information theory with bosonic systems typically involves modeling unbounded operators over infinite-dimensional Hilbert spaces with continuous spectrum, and is thus often referred to as continuous-variable quantum information theory26,27,28. In this framework, systems corresponding to individual quantum harmonic oscillators are called qumodes, or simply modes, and quantum states of m-mode bosonic systems are elements of an infinite-dimensional Hilbert space \({{{\mathcal{H}}}}^{\otimes m}\), with each single-mode Hilbert space spanned by a countably infinite (Fock) basis \({\{\left\vert n\right\rangle \}}_{n\in {\mathbb{N}}}\).

Creation and annihilation operators \({\hat{a}}^{{\dagger} }\) and \(\hat{a}\) for each mode are defined by their action on the Fock basis as \({\hat{a}}^{{\dagger} }\left\vert n\right\rangle=\sqrt{n+1}\left\vert n+1\right\rangle\), \(\hat{a}\left\vert n+1\right\rangle=\sqrt{n+1}\left\vert n\right\rangle\) and \(\hat{a}\left\vert 0\right\rangle=0\). The (unbounded) canonical bosonic operators are then given by \(\hat{q}=\frac{1}{\sqrt{2}}(\hat{a}+{\hat{a}}^{{\dagger} })\) and \(\hat{p}=\frac{1}{i\sqrt{2}}(\hat{a}-{\hat{a}}^{{\dagger} })\) and satisfy the canonical commutation relation \([\hat{q},\hat{p}]=i\hat{I}\), where \(\hat{I}\) is the identity operator. Polynomial Hamiltonians over m modes are the Hermitian operators of the form \(P({\hat{q}}_{1},{\hat{p}}_{1},\ldots,{\hat{q}}_{m},{\hat{p}}_{m})\), where P is a polynomial and where \(({\hat{q}}_{1},{\hat{p}}_{1},\ldots,{\hat{q}}_{m},{\hat{p}}_{m})\) are the canonical operators of the modes 1, …, m. The number operator is defined as \({\hat{n}}={\hat{a}}^{{\dagger} }{\hat{a}}\), and its expectation value is the average particle number of a bosonic mode, which we refer to as energy hereafter. For all \(d\in {\mathbb{N}}\), we denote by \({{{\mathcal{H}}}}_{d}: \!\!={{\rm{span}}}{\{\left\vert n\right\rangle \}}_{0\le n\le d}\) the subspace of states with a number of particles at most d.

In some sense, not all states in the Hilbert space are valid physical states, even if they are normalized: for instance, some may have infinite energy, such as \(\sqrt{6}{\sum }_{n\ge 1}\frac{1}{\pi n}\left\vert n\right\rangle\). Similarly, there are normalized states with infinite fluctuations in either position or momentum or both. To avoid inconsistencies and ensure that the action of polynomial Hamiltonians leads to physical states, it is common to define a set of physical states as a dense subspace of the Hilbert space known as the Schwartz space20—informally, the set of states with bounded canonical operator moments, with a position wave function and all of its derivatives decaying sufficiently fast at infinity, which we denote by \({{\mathcal{S}}}\subset {{\mathcal{H}}}\) (see the Methods section). Similarly, denoting by \({{\mathcal{U}}}({{\mathcal{H}}})\) the group of unitary operators over \({{\mathcal{H}}}\), we define

$${{\mathcal{U}}}({{\mathcal{S}}}) : \!\!=\left\{{\hat{U}}\in {{\mathcal{U}}({{\mathcal{H}}})\,| \,\forall \left\vert \psi \right\rangle \in {{\mathcal{S}}},\,{\hat{U}}\left\vert \psi \right\rangle \in {{\mathcal{S}}}}\right\}.$$

(1)

These form a group of physical unitary operators, i.e., which map physical states to physical states. This set can be readily extended to the multimode setting. Physical unitary operators have the property that they map bosonic states with a finite number of particles to states of finite energy: for all \(n\in {\mathbb{N}}\) and all \(\hat{U}\in {{\mathcal{U}}}({{\mathcal{S}}})\),

$${E}_{\hat{U}}(n) : \!\!={\sup }_{\left\vert \psi \right\rangle \in {{{\mathcal{H}}}}_{n}}\left\langle \psi \right\vert {\hat{U}}^{{\dagger} }\hat{n}\hat{U}\left\vert \psi \right\rangle < +\infty .$$

(2)

In that case, the supremum is a maximum and the quantity \({E}_{\hat{U}}(n)\) can be thought of as the maximal amount of energy involved when implementing the unitary evolution \(\hat{U}\) of an initial state with a number of particles at most n. This is a slightly weaker property than energy-limited quantum dynamics29 which map state of finite energy to states of finite energy.

We denote by \(D(\rho,\sigma )=\frac{1}{2}\parallel \rho -\sigma {\parallel }_{1}\) the trace norm distance between density operators22, which is used to define the diamond norm for quantum maps. The diamond norm induces a distinguishability measure between maps that is often too stringent for quantum mechanical applications involving unbounded operators, as physical unitary channels may be always maximally separated for this norm, even though they may have similar effects on all states below a certain energy30. Instead, the strong topology of pointwise convergence provides a suitable notion of continuity in infinite dimensions, which is implied by the closeness in energy-constrained diamond norm (see the Methods section), defined as31:

$$\parallel {{\mathcal{E}}}{\parallel }_{\diamond }^{E} : \!\!={\sup }_{{{\rm{Tr}}}[\rho (\hat{H}\otimes {\hat{I}})]\le E}\parallel ({{\mathcal{E}}}\otimes {{\rm{id}}})\rho {\parallel }_{1}.$$

(3)

Here, \({{\mathcal{E}}}\) is a Hermitian-preserving map, ρ is a density operator over \({{\mathcal{H}}}\otimes {{{\mathcal{H}}}}^{{\prime} }\), with \({{{\mathcal{H}}}}^{{\prime} }\) isomorphic to \({{\mathcal{H}}}\), and \(\hat{H}\) is a Hamiltonian over \({{\mathcal{H}}}\) with ground state energy equal to 0 used to specify the energy bound E > 0. We employ this topology hereafter, with \(\hat{H}=\hat{n}\) the number operator.

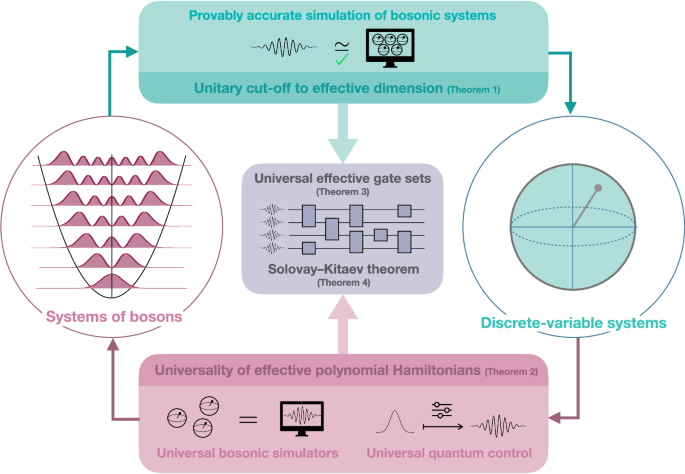
Effective dimension of physical unitary evolutions

Having introduced the necessary notation, we show in this section that any physical unitary channel can be approximated to arbitrary precision by a finite-dimensional unitary channel, where the quality of the approximation is measured by the energy-constrained diamond norm. This is captured by the notion of approximate effective dimension, which we define as follows:

Definition 1

(Approximate effective dimension). Let \(\hat{U}\) be a single-mode unitary operator, let E≥0 be an energy parameter, and let ϵ > 0 be an approximation parameter. Let also \(d\in {\mathbb{N}}\). The unitary operator \(\hat{U}\) has (E, ϵ)-approximate effective dimension d + 1 if there exists a unitary operator \({\hat{V}}_{d}\) over \({{{\mathcal{H}}}}_{d}\) which approximates \(\hat{U}\) in the following sense: for any unitary operator \({\hat{V}}^{{\prime} }\) over \({{\rm{span}}}{(\left\vert n\right\rangle )}_{n\ > \ d}\), denoting \(\hat{V}={\hat{V}}_{d}\oplus {\hat{V}}^{{\prime} }\), \({{\mathcal{V}}}=\hat{V}{{\boldsymbol{\cdot }}}{\hat{V}}^{{\dagger} }\) and \({{\mathcal{U}}}=\hat{U}{{\boldsymbol{\cdot }}}{\hat{U}}^{{\dagger} }\),

$$\parallel {{\mathcal{U}}}-{{\mathcal{V}}}{\parallel }_{\diamond }^{E}\le \epsilon .$$

(4)

When that is the case, we say that \({\hat{V}}_{d}\) is a (d + 1)-dimensional (E, ϵ)-approximation of \(\hat{U}\).

When a unitary dynamics has a finite approximate effective dimension, it can effectively be modeled by a finite-dimensional unitary evolution. We now give our first main result:

Theorem 1

(Effective dimension of physical unitary channels). Let \({{\mathcal{U}}}=\hat{U}{{\boldsymbol{\cdot }}}{\hat{U}}^{{\dagger} }\) be a single-mode unitary channel, with \(\hat{U}\in {{\mathcal{U}}}({{\mathcal{S}}})\) a physical unitary operator. Let E≥0 be an energy parameter, and let ϵ > 0 be an approximation parameter. Then, there exists \(d={{\mathcal{O}}}\left(\frac{E}{{\epsilon }^{4}}{E}_{\hat{U}}\left(\frac{64E}{{\epsilon }^{2}}\right)\right)\in {\mathbb{N}}\) such that \(\hat{U}\) has (E, ϵ)-approximate effective dimension d + 1. Moreover, a finite-dimensional (E, ϵ)-approximation of \(\hat{U}\) can be computed in polynomial time in d, E, and \(\frac{1}{\epsilon }\).

The proof of this result is based on constructing a good unitary operator approximation of a truncated unitary operator, while carefully controlling truncation parameters for the state space, before and after applying the unitary channel, so that the truncated unitary operator is itself a good approximation of the original unitary operator. We refer to the Methods section for the main techniques and to the Supplementary Information for the proof.

A direct consequence of Theorem 1 is that the corresponding sequence of (E, ϵ)-approximations strongly converges to \(\hat{U}\) as ϵ goes to 0 in trace distance (see the Methods section). From an operational standpoint, this implies that we can effectively truncate the Hilbert space of physical bosonic computations to a certain effective dimension, as long as the cut-off is high enough. As such, Theorem 1 provides rigorous bounds on the effective dimension required to simulate bosonic dynamics with provable accuracy9. In other words, there will be no catastrophic loss of information in the measurements statistics when restricting to the cut-off evolution: by the operational property of the trace distance, results of a cut-off bosonic computation will be indistinguishable from results of the original computation. However, this cut-off comes at a price: Theorem 1 identifies a direct relation between the effective dimension sufficient to embed a unitary evolution to a good precision and the energy \({E}_{\hat{U}}\) of the unitary evolution, as defined in Eq. (2). Such an energy bound may grow very fast for seemingly simple dynamics, such as alternating Gaussian and non-Gaussian unitary evolutions25. We give an explicit construction in the Supplementary Information showing that this growth may be arbitrarily fast.

Universality of polynomial Hamiltonians

We have shown that bosonic unitary evolutions may be well approximated by finite-dimensional ones. In this section, we give our second main result, namely that any finite-dimensional Hamiltonian generating such a finite-dimensional unitary evolution can be realized exactly by a polynomial Hamiltonian:

Theorem 2

(Finite-dimensional universality of polynomial Hamiltonians). Let \(d\in {\mathbb{N}}\) and let \(\hat{H}\) be a Hermitian operator over \({{{\mathcal{H}}}}_{d}\). There exists a polynomial Hamiltonian \({P}_{\hat{H}}(\hat{q},\hat{p})\) of degree at most 3d over \({{\mathcal{H}}}\) such that

$${P}_{\hat{H}}(\hat{q},\hat{p})=\hat{H}\oplus {\hat{H}}^{{\prime} },$$

(5)

where \({\hat{H}}^{{\prime} }\) is a Hermitian operator over \({{\rm{span}}}{(\left\vert n\right\rangle )}_{n\ > \ d}\). In particular, \({P}_{\hat{H}}(\hat{q},\hat{p})\) generates an evolution in \({{\mathcal{H}}}\) given for all \(\left\vert \psi \right\rangle \in {{{\mathcal{H}}}}_{d}\) by

$${e}^{i{P}_{\hat{H}}(\hat{q},\hat{p})}\left\vert \psi \right\rangle={e}^{i\hat{H}}\left\vert \psi \right\rangle,$$

(6)

Moreover, the polynomial \({P}_{\hat{H}}\) can be computed in polynomial time in d.

The proof of this result is based on the use of interpolation polynomials for reproducing exactly a target finite-dimensional operator on a subspace of the Fock basis, taking advantage of the sparsity of the canonical operators in that basis. We refer to the Methods section for the main techniques and to the Supplementary Information for the multimode generalisation of Theorem 2 and its proof. In particular, defining the unitary evolution operator \({e}^{i{P}_{\hat{H}}(\hat{q},\hat{p})}\) on \({{\mathcal{H}}}\) is highly non-trivial: we restrict its action to states in \({{{\mathcal{H}}}}_{d}\) to avoid such mathematical technicalities.

An important consequence of this theorem is that polynomial Hamiltonians allow us to explore the full Hilbert space, i.e., there are no inaccessible regions of the Hilbert space when starting from a fixed reference state, such as the vacuum state, and restricting to using gates generated by polynomial Hamiltonians:

Corollary 1

(Universal quantum controllability of polynomial Hamiltonians in infinite dimension). Let \(\left\vert \psi \right\rangle \in {{\mathcal{H}}}\). For all ϵ > 0, there exists a polynomial Hamiltonian \({P}_{\epsilon }(\hat{q},\hat{p})\) such that evolving the vacuum state \(\left\vert 0\right\rangle\) under the Schrödinger equation with Hamiltonian \({P}_{\epsilon }(\hat{q},\hat{p})\) for constant time yields a state \(\left\vert {\psi }_{\epsilon }\right\rangle\) satisfying \(D(\left\vert \psi \right\rangle,\left\vert {\psi }_{\epsilon }\right\rangle )\le \epsilon\).

Corollary 1 proves the universal quantum controllability of polynomial Hamiltonians in infinite dimensions, resolving the open question in21 and [ref. 25, Open question 3]. We give a quick proof in the single-mode case hereafter, the multimode case being analogous.

Proof

Since the state \(\left\vert \psi \right\rangle\) is normalized, there exists dϵ such it is ϵ-close in trace distance to the state truncated at dϵ and renormalized, which we denote by \(\left\vert {\psi }_{\epsilon }\right\rangle\). Then, there exists a finite-dimensional unitary operator \({\hat{U}}_{\epsilon }={e}^{i{\hat{H}}_{\epsilon }}\) over \({{{\mathcal{H}}}}_{{d}_{\epsilon }}\) which maps \(\left\vert 0\right\rangle\) to \(\left\vert {\psi }_{\epsilon }\right\rangle\). By Theorem 2, the polynomial Hamiltonial \({P}_{\epsilon }({\hat{q}}, {\hat{p}}) : \!\!={P}_{{\hat{H}}_{\epsilon }}({\hat{q}},{\hat{p}})\) satisfies \({P}_{\epsilon }({\hat{q}},{\hat{p}})={\hat{H}}_{\epsilon }\oplus {\hat{H}}_{\epsilon }^{{\prime} }\). Evolving the vacuum under the Schrödinger equation with Hamiltonian \({P}_{\epsilon }(\hat{q},\hat{p})\) thus leads to the same state as if evolving the vacuum under the (dϵ + 1)-dimensional Schrödinger equation with Hamiltonian \({\hat{H}}_{\epsilon }\), which concludes the proof. □

Beyond quantum state preparation, Theorem 2 provides a universal method for exactly reproducing any finite-dimensional Hamiltonian using polynomial Hamiltonians. This method can be used to engineer universal bosonic simulators capable of emulating the unitary evolution of any discrete-variable quantum system.

Furthermore, Theorem 2 also implies that bosonic circuits composed of input vacuum state, unitary gates generated by polynomial Hamiltonians, and number measurements, can simulate universal qudit computations efficiently (without requiring feed-forward of measurement outcomes), generalizing a recent result for qubit computations [ref. 25, Theorem 4.1].

Effective bosonic computations

In this section, we explore the combined consequences of Theorem 1 (effective dimensions) and Theorem 2 (effective Hamiltonians) for the validity of effective descriptions of bosonic computations. At a fundamental level, both results show that effective descriptions are capturing bosonic computations well, i.e., one can always truncate the dimension of physical unitary evolutions up to an arbitrarily small error and use polynomial Hamiltonians to model finite-dimensional evolutions exactly. Together, these two results imply that polynomial Hamiltonians can generate any physical unitary evolution approximately to arbitrary precision:

Theorem 3

(Infinite-dimensional universality of polynomial Hamiltonians). Let \({{\mathcal{U}}}=\hat{U}{{\boldsymbol{\cdot }}}{\hat{U}}^{{\dagger} }\) be a single-mode unitary channel, with \(\hat{U}\in {{\mathcal{U}}}({{\mathcal{S}}})\) a physical unitary operator. Let E≥0 be an energy parameter, and let ϵ > 0 be an approximation parameter. Then, there exists \(d={{\mathcal{O}}}\left(\frac{E}{{\epsilon }^{4}}{E}_{\hat{U}}\left(\frac{64E}{{\epsilon }^{2}}\right)\right)\in {\mathbb{N}}\) and a polynomial Hamiltonian \(P(\hat{q},\hat{p})\) of degree at most 3d such that, writing \({{\mathcal{V}}}\) the corresponding unitary evolution induced on \({{{\mathcal{H}}}}_{d}\),

$$\parallel {{\mathcal{U}}}-{{\mathcal{V}}}{\parallel }_{\diamond }^{E}\le \epsilon .$$

(7)

Moreover, the polynomial P can be computed from \(\hat{U}\) in polynomial time in d, E, and \(\frac{1}{\epsilon }\).

As we explain in the Methods section, this result is a direct consequence of Theorem 1 and Theorem 2. Formally, Theorem 3 shows that the group of unitary gates generated by polynomial Hamiltonians is dense in the group of physical unitary operators in the strong operator topology (see the Methods section). This places the definition of universality for continuous-variable quantum gate sets, based on the ability to approximate to arbitrary precision any unitary evolution generated by a polynomial Hamiltonian11, on an equal footing with its discrete-variable counterpart, based on the property to approximate to arbitrary precision any unitary operation22.

As such, this shows that polynomial Hamiltonians generate truly universal gate sets and paves the way for a Solovay–Kitaev theorem23 in the infinite-dimensional setting. We obtain a version of this theorem hereafter, for universal gate sets generated by polynomial Hamiltonians as in Theorem 2:

Theorem 4

(Solovay–Kitaev theorem for polynomial Hamiltonians). Let E > 0, ϵ > 0 and \(d\ge \frac{64E}{{\epsilon }^{2}}\in {\mathbb{N}}\). Let \({{\mathcal{G}}}\) be a finite set of unitary operators over \({{{\mathcal{H}}}}_{d}\) generating a dense subset of \({{\mathcal{U}}}({{{\mathcal{H}}}}_{d})\) and let \({{\mathcal{P}}}\) be its realization with polynomial Hamiltonians from Theorem 2. There is a constant c such that for any physical unitary operator \(\hat{U}\in {{\mathcal{U}}}({{\mathcal{S}}})\) with (E, ϵ)-approximate effective dimension d + 1, there exists a finite sequence \(\hat{V}\) of gates from \({{\mathcal{P}}}\) of length \({{\mathcal{O}}}({\log }^{c}(1/\epsilon ))\) and such that \(\parallel {{\mathcal{U}}}-{{\mathcal{V}}}{\parallel }_{\diamond }^{E}\le 2\epsilon\), where \({{\mathcal{U}}}=\hat{U}{{\boldsymbol{\cdot }}}{\hat{U}}^{{\dagger} }\) and \({{\mathcal{V}}}=\hat{V}{{\boldsymbol{\cdot }}}{\hat{V}}^{{\dagger} }\).

Recall that Theorem 1 ensures the existence of an (E, ϵ)-approximate effective dimension for all physical unitary operators. The proof of Theorem 4 combines Theorems 1 and 2 with the Solovay–Kitaev theorem for qudits23 of dimension d + 1, and provides an explicit algorithm for producing the sequence of polynomial Hamiltonians, given the target unitary \(\hat{U}\in {{\mathcal{U}}}({{\mathcal{S}}})\). We refer to the Methods section for the main techniques and to the Supplementary Information for the proof.

Theorem 4 generalises the Gaussian Solovay–Kitaev theorem from ref. 24, thus providing an answer to [25, Open question 4] for the gate sets based on the polynomial Hamiltonians used in Theorem 2. In particular, it implies the computational equivalence of bosonic quantum circuits based on these universal gate sets.