Experimental configuration
Figure 1a shows a general schematic of the experiment. Two remote QDs are used: QD1 functions as a single-photon source (SPS), emitting Photon 1. QD2 serves as an entangled pair source (EPS), emitting an entangled photon pair: Photon 2 and Photon 3. In both cases, the QDs are excited via pulsed two-photon excitation and generate photons via the biexciton-exciton cascade (\(\left\vert XX\right\rangle \to \left\vert X\right\rangle \to \left\vert G\right\rangle\))66,67,68. The biexciton (XX) photons (Photon 1 and Photon 2) are sent to a BSM setup, after two distinct quantum frequency conversion (QFC) processes (see methods), while the exciton (X) emission of QD2 (Photon 3) is analyzed. The joint BSM projects Photon 1 and Photon 2 onto a maximally entangled Bell state, teleporting the polarization state of Photon 1 (named \({\left\vert \xi \right\rangle }_{1}\)) onto Photon 3. The receiver reconstructs the polarization state of Photon 3 (named \({\left\vert \xi \right\rangle }_{3}\)) conditioned on the BSM result.
Fig. 1: Quantum teleportation setup.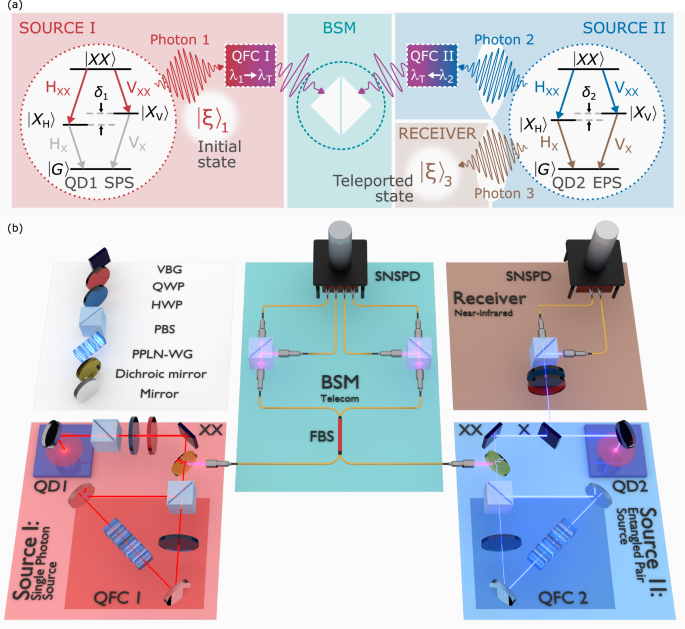
a Schematic of the experiment where QD1 is used as a single-photon source (SPS), while QD2 is used as an entangled pair source (EPS). Two independent quantum frequency converters (QFC) are employed to convert the biexciton photons to a common telecommunication wavelength. After the Bell state measurement (BSM), the state of the single photon (named \({\left\vert \xi \right\rangle }_{1}\)) is teleported onto the non-interfering exciton photon. b 3D sketch of the setup: QD1 generates a single biexciton photon, which is prepared in \({\left\vert \xi \right\rangle }_{1}\) using a polarizing beamsplitter (PBS) followed by a half (HWP) and quarter-wave plate (QWP), and spectrally filtered with a volume Bragg grating (VBG). The photon is frequency converted to telecommunication wavelength using polarization-preserving quantum frequency conversion, employing a periodically-poled lithium niobate waveguide (PPLN-WG), and sent to a fiber beamsplitter (FBS) for the BSM. QD2 generates an entangled photon pair: while the exciton photon is sent to the near-infrared receiver, the biexciton is frequency converted to match the wavelength of the converted biexciton photon of QD1. Polarizing beamsplitters are used in the BSM and receiver side before detection on superconducting nanowire single-photon detectors (SNSPDs).
Figure 1b depicts a detailed illustration of the experimental configuration. During the experimental procedure, a pulsed laser (304.8 MHz repetition rate corresponding to a 3.28 ns repetition period) coherently prepares a XX state in two epitaxially grown droplet etching GaAs QDs29,30 remotely located in different cryostats. The excitation is followed by a cascaded emission of two polarization-entangled photons at NIR wavelengths (~780 nm). The polarization state \({\left\vert \xi \right\rangle }_{1}\) of Photon 1 (to be teleported) is prepared by sending it through a polarizing beamsplitter (PBS), followed by a half- (HWP) and a quarter-wave plate (QWP). Photon 2 and Photon 3 share a maximally entangled oscillating state \(1/\sqrt{2}\left({\left\vert HH\right\rangle }_{2,3}+{e}^{i{\delta }_{2}t/\hslash }{\left\vert VV\right\rangle }_{2,3}\right)\), where \(\left\vert H\right\rangle\) (\(\left\vert V\right\rangle\)) represents horizontal (vertical) polarization, δ2 the fine-structure splitting (FSS) of the EPS, t the time between XX and X emission, and ℏ the reduced Planck constant. For slow FSS-induced oscillations (here δ2 = 2.1(3) μeV) relative to the emitter decay time, the latter state can be simplified to a maximally entangled Bell state \({\left\vert {\Phi }^{+}\right\rangle }_{2,3}=1/\sqrt{2}\left({\left\vert HH\right\rangle }_{2,3}+{\left\vert VV\right\rangle }_{2,3}\right)\) (for more details see Supplementary Note 1G). The wavelengths of Photon 1 and Photon 2 at ~ 780 nm do not spectrally overlap, prohibiting interference. To enable two-photon interference required for a successful BSM, polarization-preserving QFC is employed (see Fig. 1b and methods)65. This process converts the XX photons (Photons 1 and 2) to a common telecommunication wavelength (1515 nm, see Fig. 2a), leaving their quantum state unaltered. Being at technologically relevant telecommunication wavelengths also opens the way for prospective long-distance teleportation experiments. After interference, the (three-photon) state can be written in the Bell basis:
$$\begin{array}{rcl}\left\vert {\Psi }_{{{\rm{tot}}}}\right\rangle={\left\vert \xi \right\rangle }_{1}\otimes {\left\vert {\Phi }^{+}\right\rangle }_{2,3}=\frac{1}{2}\left({\left\vert {\Phi }^{+}\right\rangle }_{1,2}{\left\vert \xi \right\rangle }_{3}+{\left\vert {\Phi }^{-}\right\rangle }_{1,2}{\sigma }_{3}{\left\vert \xi \right\rangle }_{3}\right.\\ \left.+{\left\vert {\Psi }^{+}\right\rangle }_{1,2}{\sigma }_{1}{\left\vert \xi \right\rangle }_{3}-{\left\vert {\Psi }^{-}\right\rangle }_{1,2}{\sigma }_{1}{\sigma }_{3}{\left\vert \xi \right\rangle }_{3}\right),\end{array}$$
(1)
with Pauli matrices σ1 and σ3 (for exemplary calculations see Supplementary Note 2B) and Bell states \({\left\vert {\Phi }^{\pm }\right\rangle }_{1,2}=1/\sqrt{2}\left({\left\vert HH\right\rangle }_{1,2}\pm {\left\vert VV\right\rangle }_{1,2}\right)\) and \({\left\vert {\Psi }^{\pm }\right\rangle }_{1,2}=1/\sqrt{2}\left({\left\vert HV\right\rangle }_{1,2}\pm {\left\vert VH\right\rangle }_{1,2}\right)\). Here, the BSM unit is implemented as a single-mode fiber beamsplitter (FBS) with a PBS at each output arm, followed by superconducting nanowire single-photon detectors (SNSPDs). In this polarization-selective BSM configuration the projections of Photon 1 and Photon 2 onto Bell states \({\left\vert {\Psi }^{+}\right\rangle }_{1,2}\) or \({\left\vert {\Psi }^{-}\right\rangle }_{1,2}\) can be identified, increasing the BSM efficiency considerably45,69. A successful BSM heralds the unitary transformation to be applied to Photon 3 to reconstruct the initially prepared quantum state of Photon 1 (see Supplementary Note 2B). To probe the teleported polarization state \({\left\vert \xi \right\rangle }_{3}\), Photon 3 is analyzed with a tomography unit consisting of a QWP, a HWP followed by a PBS, and two SNSPDs. In the following, the results for one projection onto \({\left\vert {\Psi }^{-}\right\rangle }_{1,2}\) are discussed (other combinations can be found in Supplementary Note 3). For Photon 1, 2, and 3, the single-photon count rates at the detector (summed over all measuring detectors) are B1 = 12.5 kHz, B2 = 20.0 kHz and B3 = 625 kHz. In Supplementary Note 1I and 1J, a detailed quantification of setup and source efficiencies is provided.
Fig. 2: Linewidth and interference of remote quantum light sources.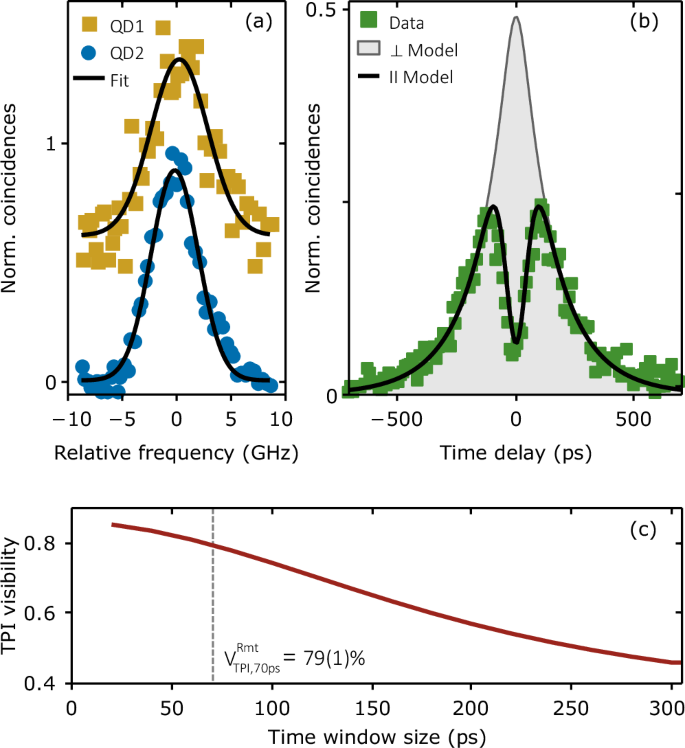
a High-resolution linewidth measurements of the QDs biexciton emissions (\(\left\vert H\right\rangle\) component) after quantum frequency conversion, recorded with a Fabry-Pérot interferometer, also depicting their spectral overlap. The data points depict the measured results, and the solid lines are a Gaussian fit function. The data are shifted in the y-direction for clarity. b The center peak of a remote two-photon-interference (TPI) experiment between Photon 1 and Photon 2 with parallel polarization (green squares) is shown (see Supplementary Note 1H for full histogram). A model function as proposed by ref. 79 is used to fit these data (solid black line). The orthogonal polarization setting (gray area) is deduced from the fit results of the parallel setting. c Temporally post-selected remote two-photon-interference visibility \({V}_{\,{\rm{TPI}}}^{{\rm{Rmt}}\,}\) calculated from the fit results given in (b). The time window is centered around zero time delay.
Two-photon interference after quantum frequency conversion
Two key requirements for successful quantum teleportation are a high degree of entanglement of the EPS45 and a high indistinguishability between the two XX photons entering the BSM. The former is intrinsic to the employed QD structure, and it is maintained by the QFC setup (entanglement fidelities up to 0.97, see Supplementary Note 1G). The latter is mainly achieved thanks to the erasure of the initial frequency mismatch between the remote interfering XX photons via the precise spectral tuning of the pump fields in the QFC processes (being the interference visibility only eventually limited by the pumping scheme and spectral broadening).
Figure 2a depicts a high-resolution spectrum of the XX emission lines of QD1 and QD2 at telecommunication wavelength after frequency matching during QFC. A Gaussian fit function provides a linewidth of 5.2(4) GHz (4.3(1) GHz) for QD1 (QD2). The two given lines have a relative spectral offset of 0.43(27) GHz, due to pump laser drifts in the QFC setup. Decay-time measurements (\({\tau }_{\,{\rm{XX}}}^{{\rm{QD}}\,1,2}\) = 176 ps, 120 ps) suggest the photon Fourier limit to be at 0.903(10) GHz and 1.322 (5) GHz. The deviation of the measured linewidth from the Fourier limit is caused by inhomogeneous spectral broadening mechanisms70,71 and suffices for a Gaussian approximation in the fit. The indistinguishability of the two converted emissions is probed by a two-photon-interference (TPI) experiment at the outputs of the FBS with linear polarized photons. The central peak of the correlation measurement is shown as green data points in Fig. 2b. From this, the remote TPI visibility \({V}_{\,{\rm{TPI}}}^{{\rm{Rmt}}\,}\) is evaluated (following ref. 63 and references therein). While this central peak is expected to vanish for fully indistinguishable photons, in the present case the TPI visibility is limited to 30(1)%. This has two reasons: first, the time-ordered cascade of the three-level system gives an upper limit set by the XX and X decay rates \({V}_{{{\rm{TPI}}},\max }^{\,{\rm{Rmt}}\,}={\gamma }_{XX}/({\gamma }_{XX}+{\gamma }_{X})\) = 59%72, and second, the inhomogeneous spectral broadening observed in the FPI measurements (the spectral broadening mechanisms are discussed in Supplementary Note 1C). The interference visibility can be increased through temporal post-selection, which can mitigate the impact of the two aforementioned mechanisms. Figure 2c depicts the interference visibility for an increasing time window centered around zero time delay. Indeed, the visibility of \({V}_{{{\rm{TPI}}},70\,{{\rm{ps}}}}^{\,{\rm{Rmt}}\,}\) = 79(1)% found for a time window of 70 ps (minimal post-selection time window in the teleportation experiment discussed below) drops to 30(1)% without temporal post-selection.
Teleportation of three conjugate polarization states
To perform the all-photonic teleportation experiment, Photon 1 is prepared in three conjugate polarization states \({\left\vert \xi \right\rangle }_{1}=\left\vert H\right\rangle\), \(\left\vert D\right\rangle\), and \(\left\vert R\right\rangle\), respectively. We measure three-photon coincidences between the BSM and Photon 3 for time windows ranging from 70 ps to 290 ps (the latter being a trade-off between covering the entire interference peak and minimizing unwanted background coincidences), resulting in averaged coincidence rates between 0.11(3) mHz and 2.5(7) mHz, respectively. The density matrix of the teleported state is reconstructed from the coincidence measurements (see methods and Supplementary Note 2C).
In Fig. 3a–c the fidelity of the teleported state \({\left\vert \xi \right\rangle }_{3}\) (heralded by \({\left\vert {\Psi }^{-}\right\rangle }_{1,2}\)) to the three conjugate input states is calculated. Because the TPI visibility decreases as a function of integration time, as shown in Fig. 2c, the fidelity is expected to also depend on this time window. Therefore, the fidelity is evaluated for various three-photon coincidence time windows between 70 ps and 290 ps. The data points are the measurement results with error bars given by one standard deviation of a distribution obtained via a Monte-Carlo simulation (10000 runs), assuming Poissonian statistics (see Supplementary Note 2D). In an ideal scenario when teleporting \(\left\vert H\right\rangle\) (\(\left\vert D\right\rangle\) or \(\left\vert R\right\rangle\)) one would expect the fidelity to the \(\left\vert H\right\rangle\) (\(\left\vert D\right\rangle\) or \(\left\vert R\right\rangle\)) state \({f}^{\left\vert H\right\rangle \to \left\vert H\right\rangle }\) (\({f}^{\left\vert D\right\rangle \to \left\vert D\right\rangle }\) or \({f}^{\left\vert R\right\rangle \to \left\vert R\right\rangle }\)) to be unity and the respective remaining two fidelities to be 1/2 (gray line in Fig. 3a–c). For example, a fidelity to \(\left\vert H\right\rangle\) of 1 means the photon is maximally polarized in \(\left\vert H\right\rangle\) and a fidelity to \(\left\vert R\right\rangle\) of 1/2 means the photon has no polarization component in the \(\left\vert R\right\rangle\)-\(\left\vert L\right\rangle\)-basis. In Fig. 3a the fidelity of the teleported state \(\left\vert H\right\rangle\) to state \(\left\vert H\right\rangle\) is \({f}_{70\,{{\rm{ps}}}}^{\left\vert H\right\rangle \to \left\vert H\right\rangle }=0.860(23)\) for a 70 ps time window. For longer time windows, \({f}^{\left\vert H\right\rangle \to \left\vert H\right\rangle }\) drops only slightly but stays above 0.7. The fidelity obtained when teleporting another state, shown in Fig. 3b (Fig. 3c), is \({f}_{70\,{{\rm{ps}}}}^{\left\vert D\right\rangle \to \left\vert D\right\rangle }=0.630(38)\) (\({f}_{70\,{{\rm{ps}}}}^{\left\vert R\right\rangle \to \left\vert R\right\rangle }=0.672(34)\)) and drops to 0.55 (0.6) for longer time windows. All remaining fidelities of states conjugate to the initial state of Photon 1 show deviations of ± 0.1 from 1/2. The three described teleportation experiments are modeled with theoretical simulations (see methods and Supplementary Note 4 for further details). Based on this model the two main contributors to the non-unity of fidelities \({f}^{\left\vert H\right\rangle \to \left\vert H\right\rangle }\), \({f}^{\left\vert D\right\rangle \to \left\vert D\right\rangle }\) and \({f}^{\left\vert R\right\rangle \to \left\vert R\right\rangle }\) are the limited TPI visibility and multi-photon contributions from the QFC process (anti-Stokes Raman scattered photons generated at the target wavelength73, see methods). For larger time windows, the TPI visibility drops (Fig. 2c) while the fraction of background counts increases, leading to the observed decrease in the fidelities. Higher teleportation fidelities of \({f}^{\left\vert H\right\rangle \to \left\vert H\right\rangle }\) are a result of the BSM basis choice (\(\left\vert H\right\rangle,\left\vert V\right\rangle\)) leading to additional classical correlations between the BSM and Photon 3 (see Supplementary Note 4A for a detailed explanation). Examining the corresponding density matrix ρ of the teleported state is essential to understanding the variations in conjugate fidelities. A theoretical model was developed to quantify the impact of the experimental parameters on the teleportation results (more details are given in the methods section and Supplementary Note 4A). Relying on the quantum process matrix formalism for quantum teleportation with realistic QDs45,74, this formalism provides an analytical description of the output state of the teleportation protocol, depending on the input state, and incorporates the effects of limited single-photon purity, non-zero FSS, and other decoherence processes in the QD. Here, we corrected the original output state matrix using a classical interference term that prioritizes the \(\left\vert H\right\rangle\) state as the output from the teleportation process. The weight of this correction term is determined by the polarization mode overlap Mp, which accounts for the spectral and spatial distinguishability between the \(\left\vert H\right\rangle\) and \(\left\vert V\right\rangle\) wave packets generated by the QD due to non-zero FSS and imperfect polarization mode overlap at the FBS in the BSM. The parameters of the used QDs were either determined by spectral and radiative decay measurements (decay time of exciton τX = 171 ps, dephasing time T2 = 35 ps) or fixed based on the literature on similar QD systems (cross-dephasing time \({\tau }_{HV}=\left[1,10\right]\,{{\rm{ns}}}\), spin scattering time \({\tau }_{ss}=\left[1,10\right]\,{{\rm{ns}}}\))74. In such cases, the uncertainty interval was assumed as an input for the theoretical model, as the dephasing times τHV and τss were not measured for the QD used. Figure 3d, e, and f (g, h and i) depict the measured (simulated) density matrices of the three teleported states, respectively for an exemplary time window of 70 ps around zero time delay, before application of any unitary transformation. The imbalance between the diagonal elements ρHH and ρVV in the real part of Fig. 3f, h and i arise from classical correlations, favoring the teleportation of the \(\left\vert H\right\rangle\) state due to differences in TPI visibilities for \(\left\vert H\right\rangle\) and \(\left\vert V\right\rangle\) wave packets (manifesting itself in a lowered ρHH and increased ρVV when projecting onto \({\left\vert {\Psi }^{-}\right\rangle }_{1,2}\)). This imbalance in TPI visibilities comes from the QD’s non-zero FSS, non-perfect temporal wavepacket overlap, and experimental setup birefringence, which can be described by the degree of polarization mode overlap Mp (see methods). We attribute the less pronounced imbalance between the diagonal elements ρHH and ρVV in the real part of Fig. 3e to a well-compensated experimental setup birefringence for this measurement. The measured off-diagonal elements of the real part ρHV and ρVH for the teleportation of \(\left\vert H\right\rangle\) and \(\left\vert R\right\rangle\) in Fig. 3d,f are slightly lowered compared to the theoretical model in Fig. 3g, i. For the teleportation of \(\left\vert D\right\rangle\) non-zero off-diagonals are expected (Fig. 3e,h). The off-diagonal elements are affected by decoherence processes within the QD, which are determined by factors such as non-zero FSS, cross-dephasing time τHV, spin scattering time τss, and dephasing time T2 (see Supplementary Note 4A). Additionally, the small non-zero off-diagonal elements ρHV and ρVH in the imaginary part for the teleported states \(\left\vert H\right\rangle\) and \(\left\vert D\right\rangle\) (Fig. 3d,e in comparison to Fig. 3g, h) indicate an imperfect transformation between the QD bases and the measurement bases. These effects also result in the observed deviations from 1/2 for fidelities to states conjugate to \({\left\vert \xi \right\rangle }_{1}\) in Fig. 3a–c. Calculated fidelities between the measured and modeled density matrices above 97% confirm the agreement between the experiment and the theoretical model (see Supplementary Note 4B).
Fig. 3: Teleportation of three conjugate polarization states.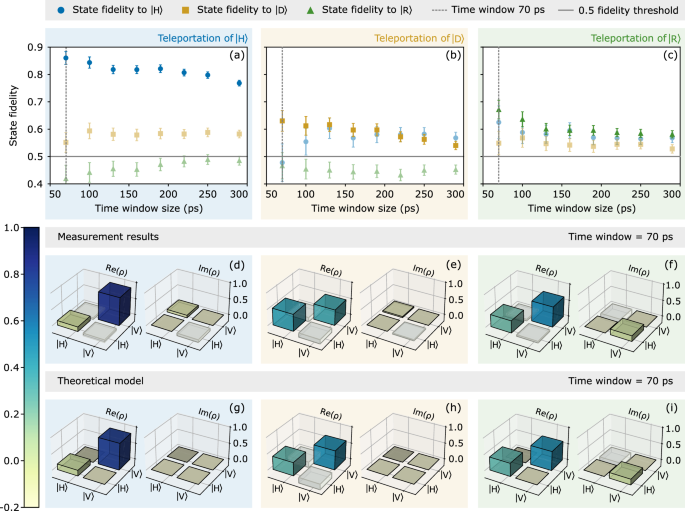
The teleportation experiment is repeated with three conjugate input states of Photon 1: \({\left\vert \xi \right\rangle }_{1}=\left\vert H\right\rangle\), \(\left\vert D\right\rangle\) and \(\left\vert R\right\rangle\) depicted in (a–c). For all three experiments, the fidelity of the measured teleported state \({\left\vert \xi \right\rangle }_{3}\) (heralded by Bell state \({\left\vert {\Psi }^{-}\right\rangle }_{1,2}\)) to the three polarization states \(\left\vert H\right\rangle\), \(\left\vert D\right\rangle\) and \(\left\vert R\right\rangle\) is shown in blue, yellow and green. The error bars correspond to one standard deviation. The solid gray line at 1/2 symbolizes zero degree of polarization in the respective basis. d–i present real \(Re\left(\rho \right)\) and imaginary parts \(Im\left(\rho \right)\) of the density matrix of the teleported state \(-{\sigma }_{1}{\sigma }_{3}{\left\vert \xi \right\rangle }_{3}\) at a 70 ps time window obtained from the measurement data (theoretical model) when teleporting \({\left\vert \xi \right\rangle }_{1}=\left\vert H\right\rangle\), \(\left\vert D\right\rangle\) and \(\left\vert R\right\rangle\) respectively, before the application of any unitary transformation. To obtain the theoretical density matrices (g–i), the following parameters were assumed in the theory model: mode overlap M = 0.85, dephasing time T2 = 35 ps, cross-dephasing time τHV = 5 ns, spin scattering time τss = 5 ns, decay time of exciton τX = 171 ps, TPI visibility V = 79% and ratio of true three-fold coincidences k = 0.85 (see methods).
From the results in Fig. 3a–c an average teleportation fidelity, denoted as \(\bar{f}=({f}^{\left\vert H\right\rangle \to \left\vert H\right\rangle }+{f}^{\left\vert D\right\rangle \to \left\vert D\right\rangle }+{f}^{\left\vert R\right\rangle \to \left\vert R\right\rangle })/3\) is determined. If one would repeat the described teleportation experiment with every possible state on the Poincaré sphere, the expected average teleportation fidelity is given by \(\bar{f}\). For this reason, the average teleportation fidelity is the figure of merit for this work. The value of \(\bar{f}\) indicates successful quantum teleportation when it exceeds the classical threshold of 2/3. Due to the polarization symmetry of our experimental configuration (supported by high entanglement fidelity after conversion and regular birefringence compensation, compare Supplementary Note 1G), we expect the fidelities for the unmeasured input states (\(\left| V\right\rangle, \left| A\right\rangle, \left| L\right\rangle\)) to be comparable to those of the measured states, making the average over three states representative. Solid dots (the red shaded area) in Fig. 4 show the average teleportation fidelity of the experimental (modeled) teleportation process, with error bars obtained via an error propagation of standard deviations. The data correspond to the state heralded by \({\left\vert {\Psi }^{-}\right\rangle }_{1,2}\). For a time window of 70 ps, the measured average teleportation fidelity \({\bar{f}}_{70{{\rm{ps}}}}\) equals 0.721(33), being 1.6 standard deviations above the classical threshold. The fidelity stays above this threshold up to 190 ps, which is longer than the employed XX photon decay time. For longer time windows, this value drops below the classical threshold, reaching a steady state at 0.630(12). Between 70 ps and 160 ps the modeled results closely reproduce the experimental findings. A divergence between the experiment and model, still within one standard deviation, occurs for longer time windows. Other BSM combinations can be found in Supplementary Note 3.
Fig. 4: Average teleportation fidelity.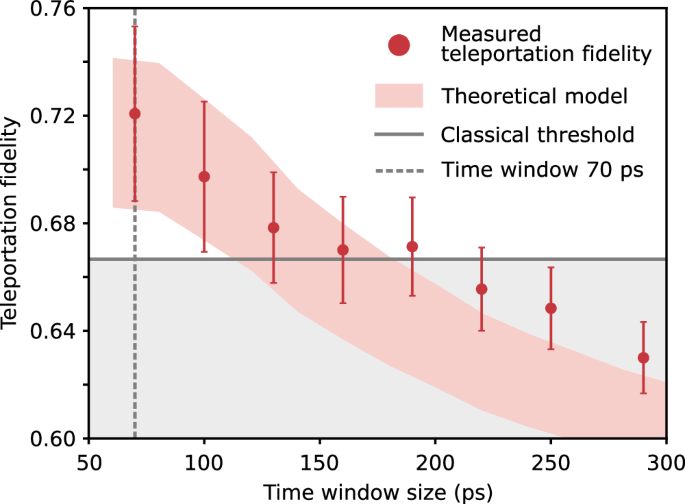
The average fidelity over all three performed teleportation experiments \(\bar{f}=({f}^{\left\vert H\right\rangle \to \left\vert H\right\rangle }+{f}^{\left\vert D\right\rangle \to \left\vert D\right\rangle }+{f}^{\left\vert R\right\rangle \to \left\vert R\right\rangle })/3\), heralded by Bell state \({\left\vert {\Psi }^{-}\right\rangle }_{1,2}\) is shown. Red solid dots represent the measured results with error bars corresponding to one standard deviation. The red shaded area shows the theoretically modeled data, and the gray solid line symbolizes the classical threshold of 2/3. The uncertainty in the theoretical model arises from some parameters that cannot be precisely determined in our experimental setting. Therefore, they were based on literature74 estimated within the following intervals to account for their variability: polarization mode overlap \({M}_{p}=\left[0.8,0.9\right]\), cross-dephasing time \({\tau }_{HV}=\left[1,10\right]\,{{\rm{ns}}}\), spin scattering time \({\tau }_{ss}=\left[1,10\right]\,{{\rm{ns}}}\). The other parameters are assumed as: dephasing time T2 = 35 ps and exciton decay time τX = 171 ps.
The results achieved show successful teleportation when temporal post-selection is applied. The requirement of post-selection is mainly due to the intrinsic performance of the utilized sources and excitation method. The error of the average teleportation fidelity is mainly impacted by the counting statistics of the sources. A higher number of threefold coincidences would decrease the width of the Poissonian distributions used for the Monte-Carlo simulation, reducing the uncertainty in the average teleportation fidelity. The divergence between the experimental and theoretical results for longer time windows is primarily due to uncertainties in the spin scattering and cross-dephasing times, which could not be directly measured for the specific QD. Additional decoherence effects not captured by the simplified process matrix may also contribute, particularly at longer time scales. Thanks to the developed theory, it is possible to quantify the impact of the experimental parameters on the average teleportation fidelity, such as TPI visibility, FSS, and single-photon purity. The average teleportation fidelity achievable with optimal QD parameters is calculated to highlight the significance of these factors, see Table 1. Among them, the TPI visibility was identified as the most crucial parameter, which must be optimized for further improvement of the average teleportation fidelity. In the case of Fourier-limited sources (as shown, e.g., for gated structures55), where the visibility of the used QD is still limited by the decay rates of the radiative cascade to \({V}_{{{\rm{TPI}}},\max }^{\,{\rm{Rmt}}\,}\) = 59% (as discussed before), the calculated fidelity surpasses the classical limit across all scenarios without requiring temporal filtering. Further improvements in TPI visibility can be achieved by incorporating a photonic structure that selectively accelerates the XX decay75. Assuming γXX = 5γX, which corresponds to a visibility of 83%, leads to an average teleportation fidelity of 0.73. Reducing the FSS and g(2)(0) further improves the achievable fidelity. The former can be minimized by mechanical strain31 or exploiting the Stark effects76. The latter can be improved by reducing the conversion-related noise with narrower spectral filtering. In such a scenario (FSS = 0, g(2)(0) = 0), an average teleportation fidelity of 0.85 could be attained. Assuming unity interference visibility, a fidelity above 0.8 is achieved in every scenario, reaching up to 0.99.
Table 1 Theoretical average teleportation fidelity as a function of linewidth, XX and X decay rates, fine-structure splitting (FSS), and g(2)(0) without temporal post-selection
