The molecular structure of Ni(p-Py-V-p-F)(H2O)5 is shown in Fig. 1a, with the Ni atom surrounded by a pyridine in p-Py-V-p-F and five water (H2O) ligand molecules, creating a six-coordinate environment. In the p-Py-V-p-F molecule, the central ring comprises four nitrogen (N) atoms with a maximum spin density22, leading to a localized spin system. Hence, the verdazyl radicals, p-Py-V-p-F, and Ni2+ ions possess spin values of 1/2 and 1, respectively. The crystallographic parameters at 100 K are as follows: monoclinic, space group Pbca, a = 8.37620(10) Å, b = 17.6025(3) Å, c = 33.8343(6) Å, V = 4988.60(14) Å3, Z = 8 (Supplementary Table 1 and Table 2). The crystal structure is isomorphic to that of \([{{\rm{Co}}}(p-{{\rm{Py}}}-{{\rm{V}}}){({{{\rm{H}}}}_{2}{{\rm{O}}})}_{5}]\cdot 2{{{\rm{NO}}}}_{3}\), forming a spin-1/2 Kondo necklace model with no chage degrees of freedom20. The MO calculations indicated predominant AF exchange interaction J1/kB = 14 K, forming a uniform spin-1/2 chain along the a axis, as shown in Fig. 1b. Each radical spin (s) in the 1D chain is coupled with the Ni spin (S) via intramolecular interactions, yielding a Kondo necklace model, as shown in Fig. 1b and c. The intramolecular interaction J2 between the verdazyl radical and the Ni2+ ion, corresponding to Kondo coupling, is expected to be of the order of 10 K, based on previous studies of the complex consisting of Ni and the verdazyl radical23. Moreover, no significant MO overlap was found between the 1D structures, enhancing the 1D nature of the Kondo necklace model (Supplementary Fig. 1 and Note 1).
Fig. 1: Crystal structure and Kondo necklace model of \([{{\rm{Ni}}}(p-{{\rm{Py}}}-{{\rm{V}}}-p-{{\rm{F}}}){({{{\rm{H}}}}_{2}{{\rm{O}}})}_{5}]\cdot 2{{{\rm{NO}}}}_{3}\).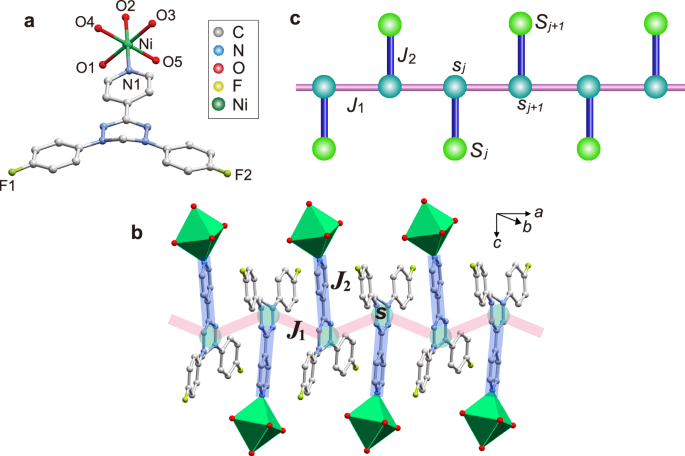
a Molecular structure of Ni(p-Py-V-p-F)(H2O)5. b Crystal structure forming the Kondo necklace model along the a axis. Hydrogen atoms are excluded to enhance clarity. The green nodes represent the spin-1/2 of the radicals. The thick lines represent exchange interactions. c, Spin-(1/2,1) Kondo necklace model comprising intermolecular J1 and intramolecular J2. s and S denote the spins on the radical and Ni2+, respectively.
Figure 2a, b show the magnetic susceptibility (χ = M/H) at 0.1 T and magnetization curve at 1.4 K. We observe a paramagnetic-like increase in χ down to 1.8 K. The magnetization curve also exhibits a paramagnetic-like behavior up to about 10 T, above which a nonlinear increase towards saturation at ~ 40 T appears. Since the value of ~ 2.2 μB/f.u. at 10 T suggests field-polarization of the Ni spins, the higher-field nonlinear behavior is expected to originate from the radical spins forming the spin-1/2 AF chain. Considering the results of MO calculations, the magnetic properties were investigated based on the spin-(1/2,1) Kondo necklace model composed of the AF interactions, J1 and J2. We calculated J2/J1 dependence of the magnetization curve using the QMC method, as shown in Fig. 2c. A clear 1/3-plateau appears for J2/J1 ≥ 1.0, indicating the full polarization of the effective spin-1/2 in the s-S dimer via J2. As J2/J1 decreases, the plateau disappears, and a drastic increase towards 2/3 magnetization becomes apparent, suggesting the full polarization of the Ni spins due to the decoupling of J2 as observed in the spin-1/2 anisotropic Kondo necklace model20. Based on the parameter dependence, we obtained a good agreement between the experimental and calculated results, leading to the evaluations of J1/kB = 20.3 K and J2/kB = 9.9 K (J2/J1 = 0.49), as shown in Fig. 2a and b. The quantitative agreement with the experimental data also confirms that possible F-site disorder has no appreciable effect on either J1 or J2.
Fig. 2: Magnetic behavior of \([{{\rm{Ni}}}(p-{{\rm{Py}}}-{{\rm{V}}}-p-{{\rm{F}}}){({{{\rm{H}}}}_{2}{{\rm{O}}})}_{5}]\cdot 2{{{\rm{NO}}}}_{3}\).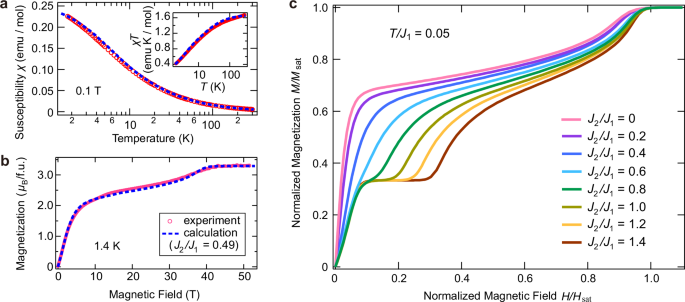
a Temperature dependence of magnetic susceptibility (χ = M/H) of \([{{\rm{Ni}}}(p-{{\rm{Py}}}-{{\rm{V}}}-p-{{\rm{F}}}){({{{\rm{H}}}}_{2}{{\rm{O}}})}_{5}]\cdot 2{{{\rm{NO}}}}_{3}\) at 0.1 T. The inset shows corrresponding χT values. b Magnetization curve of \([{{\rm{Ni}}}(p-{{\rm{Py}}}-{{\rm{V}}}-p-{{\rm{F}}}){({{{\rm{H}}}}_{2}{{\rm{O}}})}_{5}]\cdot 2{{{\rm{NO}}}}_{3}\) at 1.4 K. The dashed lines represent the QMC results for the spin-(1/2,1) Kondo necklace model with J1/kB = 20.3 K and J2/kB = 9.9 K (J2/J1 = 0.49). For the magnetization curve, a radical purity of 95 % is considered for the calculation. c Calculated magnetization curves at T/J1 = 0.05 with the representative values of J2/J1. The magnetic moment and the magnetic field are normalized by the values at the saturation. For J2/J1 ≥ 1.0, a clear 1/3 plateau emerges, reflecting full polarization of the effective spin-1/2 within the s-S dimer mediated by J2. Conversely, for J2/J1 ≪ 1.0, the magnetization exhibits a steep rise toward 2/3, consistent with full polarization of the Ni spins caused by the effective decoupling of J2.
We performed ESR measurements to examine the field-induced decoupling state of the Ni spin. Figure 3a shows the frequency dependences of the resonance signals at 1.8 K. Because the experiments were performed using the powder samples, the observed signals corresponded to the resonance fields for the external field parallel to the principal axes. We plotted the resonance fields in the frequency-field diagram, as shown in Fig. 3b. Assuming the spin-1 monomer attributed to the decoupled S, we consider the on-site anisotropy as \({{\mathcal{H}}}=D{({S}_{z})}^{2}-{\mu }_{{{\rm{B}}}}{{\boldsymbol{H}}}\widetilde{{{\bf{g}}}}{{\boldsymbol{S}}}\), where μB is the Bohr magneton, and \(\widetilde{{{\bf{g}}}}\) denotes the g-tensor. The diagonal components for the principal axes of the g-tensor are gx, gy, and gz and the other components are zero. Figure 3c show the energy levels calculated by using the evaluated parameters. The resonance modes at a sufficiently low temperature of 1.8 K correspond to the transitions indicated by the arrows in the energy branches. As shown in Fig. 3b, we obtained a good agreement between the experimental and calculated results for the resonance modes using D/kB= − 1.2 K, gx = 2.20, gy = 2.25, and gz = 2.34, demonstrating the field-induced decoupling of S.
Fig. 3: ESR of \([{{\rm{Ni}}}(p-{{\rm{Py}}}-{{\rm{V}}}-p-{{\rm{F}}}){({{{\rm{H}}}}_{2}{{\rm{O}}})}_{5}]\cdot 2{{{\rm{NO}}}}_{3}\).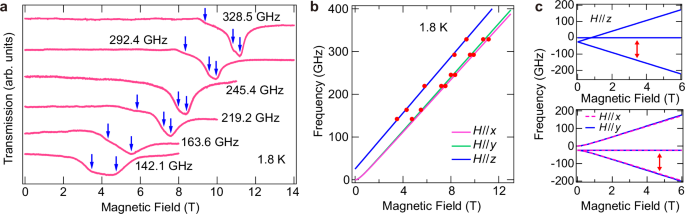
a Frequency dependence of ESR absorption spectra of \([{{\rm{Ni}}}(p-{{\rm{Py}}}-{{\rm{V}}}-p-{{\rm{F}}}){({{{\rm{H}}}}_{2}{{\rm{O}}})}_{5}]\cdot 2{{{\rm{NO}}}}_{3}\) at 1.8 K. The arrows indicate the resonance fields. b Frequency-field plot of the resonance fields. Solid lines indicate the calculated resonance modes of the spin-1 monomer along the principal axes, obtained using an on-site anisotropy of D/kB = − 1.2 K and g-values of gx = 2.20, gy = 2.25, and gz = 2.34. c Calculated energy branch of the the spin-1 monomer for H//z, H//x and H//y. Those for H//x and H//y are qualitatively equivalent. Arrows indicate spin-allowed transitions from the ground state, which correspond to the resonance modes.
Figure 4a shows the temperature dependence of specific heat Cp for H//b, perpendicular to the chain direction. The lattice contributions are not subtracted from Cp, but the magnetic contributions were expected to be dominant in the low-temperature regions considered here. At zero-field, a sharp λ-type peak appears at TN = 1.2 K, indicating a phase transition to an AF order. Note that the application of the magnetic field drastically reduces the peak value, resulting in a shift to a broad peak. Considering the field-induced decoupling of S, the broad peak corresponds to a Schottky behavior attributed to the energy gap of the spin-1 monomer. The experimental results indeed approach the behavior of the spin-1 monomer with increasing fields, as shown in Fig. 4b. Since the Cp of the spin-1 monomer for H//y most closely reproduced the experimental results, the b axis is assumed to be identical to the y axis. The higher temperature deviations are considered to arise from the spin-1/2 chain and lattice contributions. The change in the peak shape with increasing fields suggests the critical field causing the decoupling of S is ~2 T.
Fig. 4: Specific heat of \([{{\rm{Ni}}}(p-{{\rm{Py}}}-{{\rm{V}}}-p-{{\rm{F}}}){({{{\rm{H}}}}_{2}{{\rm{O}}})}_{5}]\cdot 2{{{\rm{NO}}}}_{3}\).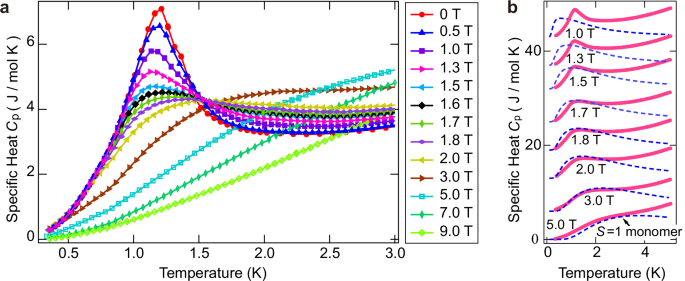
a Temperature dependence of the specific heat Cp of \([{{\rm{Ni}}}(p-{{\rm{Py}}}-{{\rm{V}}}-p-{{\rm{F}}}){({{{\rm{H}}}}_{2}{{\rm{O}}})}_{5}]\cdot 2{{{\rm{NO}}}}_{3}\) at various magnetic fields for H//b, perpendicular to the chain direction. The lines are guides for the eye. b Low-temperature region of Cp. For clarity, the values for 1.0, 1.3, 1.5, 1.7, 1.8, 2.0, and 3.0 T have been shifted up by 43, 37, 32, 25, 19, 13, and 6 J/ mol K, respectively. The broken lines represent the Schottky-type specific heat of the spin-1 monomer for H//y, obtained using an on-site anisotropy of D/kB = − 1.2 K and gy = 2.25. The experimental results approach the behavior of the spin-1 monomer with increasing fields, suggesting the critical field causing the decoupling of S is ~2 T. The higher temperature deviations are considered to arise from the spin-1/2 chain and lattice contributions.
We investigate the ground state of the spin-(1, 1/2) Kondo necklace model described by the spin Hamiltonian
$${{\mathcal{H}}}={J}_{1}\sum\limits_{j}{{{\boldsymbol{s}}}}_{j}\cdot {{{\boldsymbol{s}}}}_{j+1}+{J}_{2}\sum\limits_{j}{{{\boldsymbol{s}}}}_{j}\cdot {{{\boldsymbol{S}}}}_{j}+D\sum\limits_{j}{({S}_{j}^{z})}^{2}.$$
(1)
In the limit J2 ≪ J1, the dominant low-energy physics is governed by the spin-1/2 Heisenberg chain formed by the s spins. This system is known to exhibit a Tomonaga–Luttinger liquid (TLL) state, characterized by gapless excitations and algebraic spin correlations. To investigate the influence of the Kondo-type coupling J2 on S, we treat J2 as a perturbative parameter (Supplementary Note 2). Then, the leading contribution arises from excitations involving neighboring Kondo bonds, (sj ⋅ Sj)(sj+1 ⋅ Sj+1), which generates an RKKY-type effective interaction between neighboring S sites, i.e., \({J}_{{{\rm{eff}}}}{\sum }_{j}{{{\boldsymbol{S}}}}_{j}\cdot {{{\boldsymbol{S}}}}_{j+1}\). The resulting effective coupling constant is given by
$${J}_{{{\rm{eff}}}}=\frac{2{J}_{2}^{2}}{{\pi }^{2}{J}_{1}}\sqrt{\frac{\pi }{2}}\approx {J}_{1}{\left(\frac{{J}_{2}}{{J}_{1}}\right)}^{2}\times 0.254.$$
(2)
This expression reflects the interplay between correlations in the s chain and the s–S dimer. With the evaluated parameters, we obtain Jeff/kB ≈ 1.24K. This gives a ratio D/Jeff ≈ − 0.97, indicating that the single-ion anisotropy is strong enough to stabilize Néel order in the S sites24. Once the Sj spins develop Néel order, the Kondo coupling J2 plays an important secondary role: it acts as a staggered longitudinal field on the sj spin chain. That is, the alternating z-component of the Sj moments induces an effective staggered field on the sj sites through the Kondo interaction. As a result, the TLL state of the s chain becomes unstable and a finite staggered magnetization develops. Therefore, the Néel order initially established on the Sj sites propagates throughout the system, ultimately stabilizing a spontaneously symmetry-broken Néel order over the entire spin-(1,1/2) chain. This mechanism provides a consistent explanation for the magnetic order observed in the present study. Importantly, this behavior is fundamentally distinct from the case where the Kondo coupling acts on S = 1/2 local moments. In that situation, quantum correlations inevitably drive the system into a singlet ground state14,15,16,17,18,19,20. Such singlet formation is unavoidable for S = 1/2, and thus the emergence of Néel order through Kondo coupling is precluded. In sharp contrast, when the local moments are S≥1, the same Kondo mechanism can stabilize long-range AF order. Our present results therefore highlight a universal principle: the fate of Kondo-coupled systems is qualitatively determined by the size of the local spin, with S = 1/2 favoring singlet liquid states and S≥1 supporting magnetic order.
We now analyze the excitation state associated with the Néel order. Assuming the Néel order of S, we apply linear spin-wave theory to estimate the spin gap at zero magnetic field (Supplementary Note 3). In this framework, the excitation gap Δ corresponds to the lowest spin-wave energy and is given by
$$\Delta =\sqrt{{D}^{2}{S}^{2}+4{J}_{{{\rm{eff}}}}| D| {S}^{2}}.$$
(3)
Substituting the parameters yields a zero-field spin gap of Δ/kB ≈ 2.7K. We note that in strictly one-dimensional systems quantum fluctuations are strong, so the spin-wave approach is not quantitatively precise; here it is used only to provide a qualitative description and an appropriate energy scale. For the present system, this temperature corresponds to the regime in which effective interchain couplings can be enhanced by thermally activated magnon excitations, leading to a phase transition to a long-range order25,26. In this context, the energy scale of the observed phase transition temperature, TN ~ 1.2K, is consistent with the gap value derived from the effective spin-wave analysis.
Next we consider the effect of the applied magnetic field for H//y, which is the case for the specific heat measurements (Supplementary Note 4). In the linear spin-wave approximation, the excitation gap at k = 0 increases with the magnetic field, while the gap at k = π decreases. As in the zero-field Néel state, the canted Néel order of S is expected to induce a corresponding canted order in the s chain via the J2 interaction. This canted Néel phase becomes unstable at the critical field Hc where the magnon gap at k = π vanishes, signaling a quantum phase transition. The critical field is given by
$${H}_{c}=4{J}_{{{\rm{eff}}}}S\sqrt{1+\frac{| D| }{4{J}_{{{\rm{eff}}}}}},$$
(4)
Using the evaluated parameters, we obtain Hc ≈ 3.7T. Although this value somewhat exceeds the experimentally observed critical field of ~2T, the discrepancy can be considered reasonably small, given that the linear spin-wave approximation does not incorporate intermagonon interactions and quantum fluctuations. At Hc, the S spins are expected to decouple from the s chain, which is demonstrated in the experimental behaviors. The field-induced suppression of the Kondo coupling thus marks a phase transition from a magnetically ordered state to a quantum-disordered decoupled state. The consistency between the calculated spin gap, the critical field, and the thermodynamic measurements highlights the effectiveness of the perturbative approach in capturing the essential low-energy physics of the spin-(1,1/2) Kondo necklace model (Supplementary Note 5 and Table 3). Such field-induced destabilization of magnetic order is further facilitated by the strong quantum fluctuations inherent in one dimensionality, which naturally render the Néel state fragile. Consequently, the disappearance of the order at Hc and the emergence of TLL-like magnetization in the high-field regime are consistent with this one-dimensional character. While our present data are well explained by a decoupling scenario, the precise nature of the high-field phase remains open. Inelastic neutron scattering could directly track the gap closing and subsequent excitations, while NMR could probe local fields and spin relaxation, providing further insight into the quantum correlations of the high-field phase.
