Thermal conductivity of Fp25 and Fp75 at high pressure and room temperature
We used ultrafast time-domain thermoreflectance (TDTR) coupled with diamond-anvil cells (DACs) to precisely measure ΛFp25 and ΛFp75 to ~100 GPa at room temperature. TDTR has been widely employed to measure the thermal conductivity of various materials with high precision at various high P-T conditions (Refs. 14,22,23,24 and Methods). The unit-cell volume and spin state of Fp75 have also been complementarily characterized by synchrotron X-ray diffraction (Supplementary Note S1). As shown in Fig. 1, ΛFp25 (black symbols) starts from ~2.6 W m−1 K−1 at ambient conditions and increases with pressure until 43.1 GPa, after which it decreases by ~30% at ~54 GPa, presumably due to the pressure-induced spin transition of iron19. Upon further compression, the low-spin ΛFp25 resumes increasing with higher pressure, reaching ~25 W m−1 K−1 at 99 GPa.
Fig. 1: Pressure dependence of ΛFp25 and ΛFp75 for polycrystalline oxides at room temperature.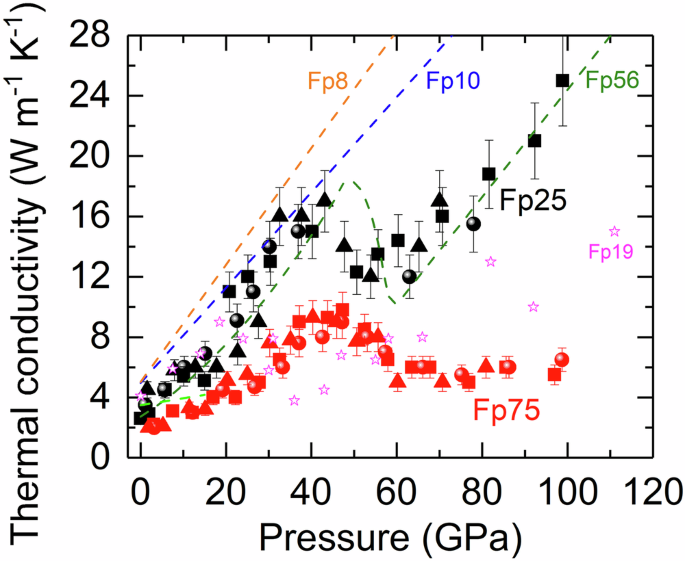
Though ΛFp25 (black symbols) and ΛFp75 (red symbols) both initially increase with compression, they present different pressure evolution. Presumably due to the spin transition of iron, the ΛFp25 decreases by ~30% at P ~ 43–54 GPa, while the ΛFp75 decreases by a larger extent of ~45% at higher pressures of P > ~ 53 GPa. In the low-spin state, the ΛFp75 has a much smaller pressure slope than the ΛFp25. Each symbol shape represents individual measurement run. The vertical bar at each datum point indicates the data uncertainty of ~10–15%. Literature results for single-crystalline Fp8 (orange dashed curve)14, Fp10 (blue dashed curve)14, and Fp56 (green dashed curve)14, as well as sintered polycrystalline Fp20 (bright green dashed line from ambient to 15 GPa)15 and Fp19 (magenta open stars)25 are plotted for comparison.
In contrast, ΛFp75 (red symbols) is systematically lower than ΛFp25, presumably resulting from the higher FeO content and Fe3+/∑Fe (see Methods), which induce stronger phonon-impurity and phonon-defect scatterings, respectively, with larger resistance to heat transport. At ambient conditions, ΛFp75 is ~1.9 W m−1 K−1, ~27% lower than ΛFp25. Under compression, ΛFp75 increases much less with increasing pressure than ΛFp25, and reaches a much lower peak value of ~8.5 ± 1 W m−1 K−1 at P ~ 40–53 GPa. Afterwards, the ΛFp75 decreases by a larger extent ( ~ 45%) and then remains approximately constant, showing a “sluggish” variation at a higher-pressure range than Fp25 through the spin transition. Finally, the low-spin ΛFp75 only increases to ~6.5 W m−1 K−1 at 99 GPa, ~4-fold lower than ΛFp25 at similar pressures.
We note that several factors could affect the ɅFp, including FeO content and ferric iron ratio (Fe3+/∑Fe) (representing impurity and defect in the crystal), and grain size. The Fp8, Fp10, and Fp56 samples in Ref. 14 are single crystals with minor amounts of ferric iron, while the Fp25 and Fp75 samples in the present study are polycrystalline powders with ~6 and ~12% ferric iron, respectively (see Methods). At ambient conditions, the ɅFp56 is expected to be lower than ɅFp25, e.g., Ref. 25. However, our data (Fig. 1) show that the present ɅFp25 seems to be comparable to the literature ɅFp56 up to ~100 GPa, but with slightly lower onset pressure for the Ʌ reduction across the spin transition. Compared to the literature Fp56 sample, the lower FeO content yet with ~6% ferric iron in the present Fp25 sample may have counter-balanced the opposite effects between FeO content (the fewer FeO, the smaller thermal resistance due to less impurity scattering) and ferric iron (the more ferric iron, the larger thermal resistance due to more defects), leading to comparable thermal conductivity. The much lower ɅFp75 along with a weaker pressure dependence in high-spin state (its low-spin state even plateaus) is therefore presumably due to the large amounts of FeO and ferric iron. In addition, using electron backscattered diffraction we found that the typical grain size of present polycrystalline Fp25 and Fp75 samples before and after high-pressure measurements were both ~15–40 μm, comparable or larger than our laser spot size in TDTR thermal conductivity measurements. We thus expect that the grain boundary plays minor roles here in affecting their thermal conductivity. Understanding the detailed, fundamental mechanisms for thermal transport in these samples in high- and low-spin states requires further advanced theoretical and computational studies.
ΛFp25 and ΛFp75 across the spin transition at elevated temperatures
To assess how elevated temperature influences ΛFp25 and ΛFp75 across the spin transition, we first compressed the sample to ~10 GPa and heated it up to 573 K (300 °C) using an externally-heated DAC (EHDAC). We then measured Λ at 573 K from ~12 to 72 GPa across the spin transition. As shown in Fig. 2, ΛFp25 at 573 K (black symbols) initially increases with pressure from 12.9 to ~35 GPa and, given the data uncertainty of ~10–15%, remains at ~11.5 ± 1 W m−1 K−1 between 35 and 46 GPa. We then observed a slight decrease ( ~ 17%) until ~56 GPa, after which the ΛFp25 re-increases with pressure to ~11.8 W m−1 K−1 at 71 GPa. Overall, in contrast to the behavior at room temperature through the spin transition (Fig. 1), the ΛFp25 at 573 K is systematically lower, with a plateau and fairly gentle decrease over a wider pressure range ( ~ 35–56 GPa). In addition, to explore its pressure dependence in the low-spin state, we have further measured the ΛFp25 at 873 K (blue symbols) in a separate experimental run, which shows a smaller pressure slope than at room temperature. Finally, ΛFp75 (red symbols) at 573 K is, again, systematically lower than the ΛFp25, with a plateau at ~6.5 ± 0.5 W m−1 K−1 at higher pressures of ~38–50 GPa. We also observed a sluggish decrease ( ~ 30%) to ~4.6 W m−1 K−1 until ~66 GPa. Though our measurement pressure was only extended to 72 GPa, the low-spin ΛFp75 seems to have a weak pressure dependence as that at room temperature.
Fig. 2: Pressure dependence of the ΛFp25 and ΛFp75 at elevated temperatures.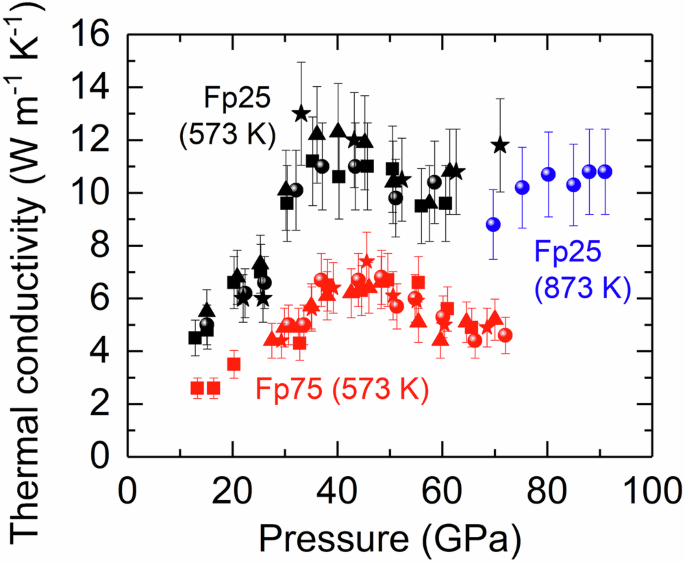
Compared to the pressure evolution at room temperature, the ΛFp25 (black symbols) and ΛFp75 (red symbols) at 573 K both soften in a more sluggish and gentle manner across the spin transition, where the pressure interval shifts to slightly higher pressures. The low-spin ΛFp25 at 873 K (blue symbols) has a weaker pressure slope than at room temperature. Each symbol shape represents individual experimental run. The vertical bar at each datum point shows its uncertainty of ~10–15%.
Since the Λ of a material scales with the square of its sound velocity14,26 (proportional to elastic constants), the pressure evolution of ΛFp25 and ΛFp75 in Figs. 1 and 2 can be primarily accounted for by the softening of elastic constants across the spin transition14,18. Moreover, compared to room temperature, the extent of decrease in Λ through the spin transition at 573 K is more sluggish, and the transition extends to higher pressures. These observations are in good agreement with the qualitative evolution of elastic constants across the spin transition at elevated temperatures as predicted by ab initio calculations18,19.
Temperature dependence of the low-spin ΛFp25 and ΛFp75
Understanding the temperature dependence of ΛFp25 and ΛFp75 in the low-spin state is critical to better constrain the deep-mantle thermal state. To this end, we explored how the low-spin ΛFp25 and ΛFp75 change with temperature to ~973 K (Fig. 3). To quantify their temperature dependence, for simplicity, we assumed that the transition to the low-spin state is complete above ~62–64 GPa and that low-spin ΛFp25 and ΛFp75 can be modelled as Λ(T) = ΛLST n, where ΛLS is a normalization constant. Such a power law dependence for Λ(T) is based on fundamental heat transport theory under Debye approximation and on an assumption that the three phonon umklapp scattering between acoustic phonons is the predominant mechanism for heat transport27,28,29,30. Since phonon relaxation time can be approximated to be inversely proportional to T, heat transport theory predicts that for a pure crystal, Λ(T) would scale with T −1, while for an impurity-bearing crystal, Λ(T) would scale with T −0.5, see Refs. 27,28,29,30 for detailed derivations of the theory for thermal conductivity at high temperatures. We determined the temperature exponent n by linearly fitting a regression line in the lnΛ-lnT plot. For low-spin ΛFp25, we found n = –0.36( ± 0.07) at P = 62–68 GPa and n = –0.41( ± 0.06) at P = 72–78 GPa (Fig. 3a), slightly weaker (less sensitive to temperature change) than the typical T –0.5 dependence for several Fe-bearing mantle minerals14,15,31,32,33,34. Note that despite the spin state, Λ(Mg,Fe)O(T) has been conventionally approximated to T –0.5 throughout the whole mantle14,15,31,33, although a T –0.24 dependence for high-spin Fp5 and Fp20 only up to 14 GPa and ~1150 K had once been reported30. Furthermore, the ΛFp75 has a much weaker temperature dependence with n ranging from –0.15( ± 0.04) to –0.3( ± 0.07), see Fig. 3b. We emphasize that our findings represent critical experimental results indicating a weaker temperature dependence for the low-spin ΛFp25 and ΛFp75 than conventionally thought. We use this result to update modelled values for the deep-mantle conditions (see discussion below).
Fig. 3: Temperature dependence of ΛFp25 and ΛFp75 in the low-spin state.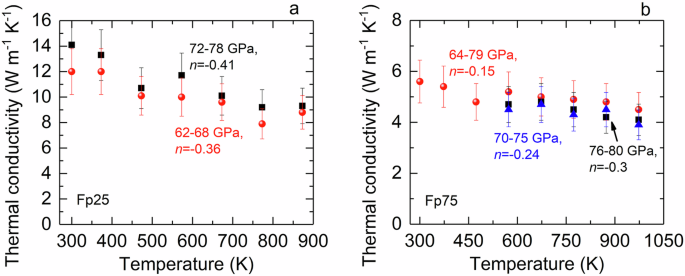
a ΛFp25 has a temperature dependence T n with n = –0.36 to –0.41, which is slightly weaker than the typical T –0.5 for Fe-bearing mantle minerals14,15,31,32,33,34. b ΛFp75 shows an even smaller temperature exponent of –0.15 to –0.3 at deep-mantle pressures. The vertical bar at each datum point represents its uncertainty of ~15%. The thermal pressure has minor effects on the temperature dependence, see Supplementary Note S2 for details.
Modelling the thermal conductivity of lower mantle minerals along a mantle geotherm
Our results for ΛFp25 and ΛFp75 with different P, T, and FeO content provide better constraints on the thermal conductivity profiles of (Mg,Fe)O and pyrolitic mantle, which in turn play a key role in the thermochemical evolution and dynamics in the deep mantle, including the impacts on LLSVPs and ULVZs. Here we first modelled ΛFp25 and ΛFp75 along a representative mantle geotherm35, to which we added a steep temperature rise from 2587 K at 2800 km depth ( ~ 130 GPa)35 to 4000 K at the CMB ( ~ 136 GPa). Furthermore, we assumed that the Λ(T) of high-spin ΛFp25 and ΛFp75 follow the typical T –0.5, while in the low-spin state they follow the trend we found in Fig. 3—i.e., ɅFp25 scales with T –0.39 and ɅFp75 scales with T –0.23. In the mixed-spin state, Λ(T) is approximated as the average of the high- and low-spin states. We find that ΛFp25 (black solid line in Fig. 4a) starts from ~4 W m−1 K−1 at 660 km and increases with depth, followed by a slight decrease across the spin transition at ~1000–1400 km depth. The low-spin ΛFp25 then reaches ~11.5 W m−1 K−1 at 2800 km depth, and slightly reduces to 10 W m−1 K−1 at the CMB due to the steep temperature rise. Compared to the conventionally assumed T –0.5 for both high- and low-spin states (black dashed line), the weaker temperature-dependence in the low-spin state (T –0.39) we found yields an ~20% higher ΛFp25 at the lowermost mantle. Moreover, we highlight that the ΛFp75 (red solid line) remains as low as ~3.6–3.8 W m−1 K−1 from ~1600–2800 km depth ( ~ 50% higher than that with the conventional T –0.5 dependence, red dashed line). The CMB’s high temperature further decreases the ΛFp75 to an exceptionally low value of ~3.4 W m−1 K−1.
Fig. 4: Modelled thermal conductivity profiles of lower mantle minerals along a representative mantle geotherm.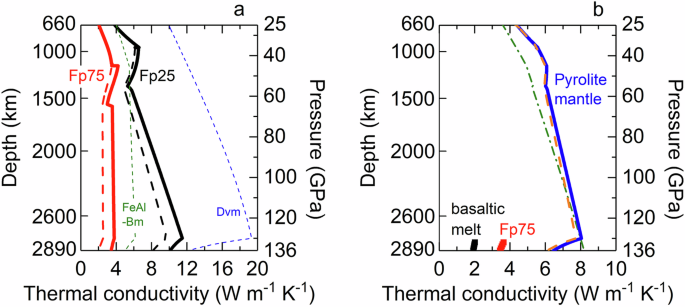
a The red solid line represents the ΛFp75 with a conventional T –0.5 dependence for high-spin state and a weaker T –0.23 dependence as we experimentally found for low-spin state, while, for comparison, the red dashed line indicates the ΛFp75 with the conventional T –0.5 dependence for both high- and low-spin states. The black solid line shows the ΛFp25 with the conventional T –0.5 dependence for high-spin state and a weaker T –0.39 dependence for low-spin state; the black dashed line is the ΛFp25 with the conventional T –0.5 dependence for both high- and low-spin states. Overall, both ΛFp25 and ΛFp75 increase with depth, except for the range where the spin transition occurs. The low-spin ΛFp75 remains nearly a constant of ~3.6–3.8 W m−1 K−1 due to its weak temperature dependence. The small artifact discontinuities at the start and end of the spin transition result from the assumed temperature dependence in the mixed-spin state. Profiles of ɅFeAl-Bm (FeAl-Bm, green dashed line) and Ʌdavemaoite (Dvm, blue dashed line) are plotted for comparison. b From the top to the bottom of the lower mantle, the ɅLM (blue solid line) increases two fold and converges to the previously modelled one (green dash-dotted line)14 at 8 W m−1 K−1 at the lowermost mantle. The sudden decrease in Ʌ profile above the CMB is due to the steep temperature rise.
Figure 4a also shows our modelled Ʌ profile of (Fe,Al)-bearing bridgmanite (FeAl-Bm) with an assumed T –0.5 dependence33 (FeAl-Bm, green dashed line) and CaSiO3 davemaoite with a T –1.1 dependence36 (Dvm, blue dashed line). Combining these two profiles with our ɅFp25 and using a Voigt-Reuss-Hill (VRH) volumetric average scheme then provide an estimate of the thermal conductivity of pyrolitic lower-mantle aggregate, ɅLM. Based on the pyrolite model, the lower mantle is composed of FeAl-Bm ( ~ 75 vol%), (Mg,Fe)O ( ~ 18 vol%), and CaSiO3 davemaoite ( ~ 7 vol%), and for calculations we assume ɅLM = 0.75ɅFeAl-Bm + 0.18ɅFp25 + 0.07Ʌdavemaoite. At ~1000 km depth, our present modelled ɅLM (blue solid line in Fig. 4b) is ~22% higher than the previously modelled profile based on room-temperature data (green dash-dotted line in Fig. 4b with a potential temperature of 2500 K14). Nevertheless, these two lines gradually converge in the deep mantle. Our modelled profile reaffirms that with the davemaoite, ɅLM is ~8 W m−1 K−114 at ~2800 km depth, but decreases to ~6.5 W m−1 K−1 at the CMB, consistent with previous results, e.g., Refs. 37,38. For comparison, we also modelled a ɅLM, where the ɅFp instead follows the conventional T –0.5, despite its spin state (orange dashed line in Fig. 4b). Because the (Mg,Fe)O only contributes ~18 vol%, the ɅLM with different Λ(Mg,Fe)O(T) in the low-spin state only differs by <4% throughout the deep mantle. For similar reasons, the variable FeO content in the (Mg,Fe)O with depth also has a minor effect on the modelled ɅLM14. Finally, the ɅLM is insensitive to the average scheme we adopted: when using Hashin–Shtrikman scheme14, the modelled ɅLM is comparable ( < ~10–15% difference) to that using the VRH scheme throughout the lower mantle.
Impacts of thermally-insulating ULVZs on the lower-mantle thermal structure and dynamics and geodynamo evolutions
The anomalously low velocities and higher density of ULVZs relative to ambient mantle imply that they are likely thermochemical heterogeneities1,2,5, e.g., Fe-rich mantle minerals, partial melts, or subducted slab materials. If made of Fe-rich oxides10,11, e.g., Fp75, ULVZs would have an exceptionally low thermal conductivity, ɅULVZ, ~3.4 W m−1 K−1 (red short stripe above 2890 km depth in Fig. 4b). This conductivity would further decrease with higher FeO content and thus, ULVZs may locally act as a thermal insulator at the CMB, meaning first that the amount of heat flowing from the core to the mantle may be limited at ULVZs locations, and second that ULVZs may have remained hot compared to their surroundings. Estimating temperature excess within ULVZs requires numerical simulations of mantle dynamics. Such excess potentially reaches several tens to a few hundreds of degrees, as suggested by temperature excess within low conductivity LLSVPs39. Such low conductivity is comparable to the previously modelled Fe-rich mantle aggregate14. Based on the results of Ref. 40, we further modelled thermal conductivity of basaltic melt at CMB-relevant high P-T conditions to be ~1.9 W m−1 K−1 (black short stripe above 2890 km depth in Fig. 4b). This value should be considered an upper bound relative to thermal conductivity of Fe-enriched melt40. If formed by heavy melt patches originated from the remnants of basal magma ocean41,42 or subducted slabs4,7, ULVZs have not only ultralow seismic velocities, but also ultralow thermal conductivity, typically about 3-fold lower than the ambient mantle.
The different thickness and amplitude of velocity and density anomalies among ULVZs observed at different locations2,4 may imply that they result from distinct formation mechanisms or are composed of different combinations of candidate materials. Recent seismic studies suggest that the internal structure of ULVZs may be complex with chemical heterogeneity and/or multilayer structures41,43, making it difficult to resolve the spatial changes in the thermal conductivity within individual ULVZ. Nevertheless, since ULVZs are small-sized and share common features of Fe-enrichment and low-velocity, these properties coherently reduce their ability to conduct heat. We thus expect that the ultralow ɅULVZ we modelled based on that of Fp75 and basaltic melt (Fig. 4b) should be reasonably representative of ɅULVZ, although, again, different ULVZs may have different origin and nature.
Our findings have important consequences on the evolution of the CMB region. The ultralow ɅULVZ with strong thermal insulating effect would promote accumulation of heat (and temperature) at their base, thus delaying cooling, which in turn further reduces Ʌ, as the Ʌ decreases with higher temperature (Fig. 3). This positive feedback mechanism results in thermal runaway that raises the local temperature, enhancing the buoyancy of ULVZs, their interactions with the surrounding LLSVPs and mantle, as well as the formation of thermal plumes rooted in ULVZs. Meanwhile, the large radial temperature gradient across the thin ULVZ patches caused by the efficient thermal insulation could produce a local, relatively cooler condition above them. Such reduced temperature may facilitate the growth of pPv above the ULVZs, and induce small-scale lateral thermal instability that could alter the regional mantle dynamics. Moreover, the thermal conductivity of the outer core, depending on its composition and investigation methods, has been suggested to a wide range of ~25–250 W m−1 K−1, e.g., Refs. 24,44,45 and references therein. Thus, within ULVZs, thermal conductivity on the mantle side of the CMB would be much lower than that on the outermost core side (Fig. 5) by at least one-order-of-magnitude. Combined with a high ULVZ temperature, TULVZ, this may significantly depress the local QCMB. Furthermore, if TULVZ is higher than the CMB temperature, local patches of negative QCMB, where heat flows from the mantle to the core, may be triggered. Such patches could in turn influence core flow, at least locally. Patches of very low or negative QCMB would further strongly increase the amplitude of lateral variations in QCMB, increasing the Q* parameter33 (defined as the ratio between the amplitude in QCMB lateral variations and twice the difference between the horizontally average QCMB and the core adiabatic heat flux). These effects would then impact the spatial and temporal evolution of the geodynamo, including the timing between polarity reversals of geomagnetic field46. Future direct experimental measurements on the thermal conductivity of (Mg,Fe)O and other candidate ULVZ materials under deep-mantle’s high P-T conditions will enable assessment of the validity of our modelled conductivity profiles and offer crucial insights to the heat transport at the lowermost mantle. Coupled with advanced numerical modelling that considers the effects of deep-mantle heterogeneities (e.g., LLSVPs, ULVZs, and slabs), these studies should bring better constraints on the complex evolution of lower-mantle thermochemical structures, the formation and growth of plumes, changes in the CMB heat flux pattern, and the stability of geodynamo.
Fig. 5: Illustration for the modelled thermal conductivity in the lower mantle.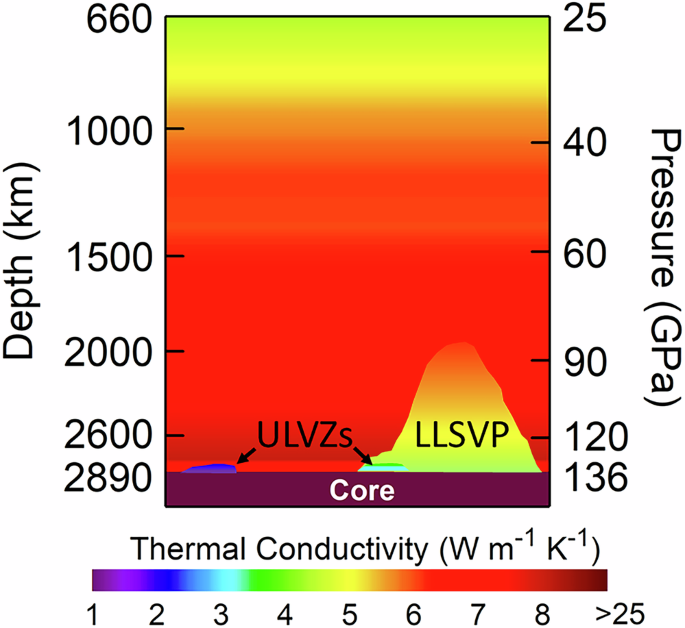
The profiles for the pyrolitic lower mantle and representative LLSVP, respectively, are from present study and Ref. 39. A ULVZ made of Fp75 and basaltic melt has an ultralow thermal conductivity of ~3.4 W m−1 K−1 and ~1.9 W m−1 K−1, respectively. A significant thermal conductivity discontinuity across the CMB is present, in particular between the ULVZ and core.
