A graphene-based quantum sensor uses two decoupled layers to form a quantized 4 × 4 Landau-level checkerboard when exposed to vertical magnetic fields. The resulting fixed δD/B spacing provides a robust signature that could enable precise detection of strong magnetic fields under cryogenic conditions.
You have full access to this article via your institution.
For many years, researchers have sought physical observables whose values are directly locked to fundamental constants. Classic milestones include the a.c. Josephson effect1, the quantum Hall effect2, and a range of topological electronic states3,4,5,6. In these systems, quantities such as conductance are fixed by immutable parameters of nature, namely Planck’s constant (h) and the elementary charge (e). The resulting conductance quantization, \({G}_{0}={e}^{2}/h\), underpins modern quantum metrology and quantum information processing. However, the number of physical variables exhibiting such quantization remains small, making the search for new quantized systems compelling for both fundamental physics and potential applications.
Now, writing in Nature Sensors, Han and co-workers report a quantized quantity: the ratio of the electric displacement field (D = εE with ε being the permittivity) to the magnetic field, D/B, quantized to e2/h in decoupled bilayer graphene twisted by a large angle7. In the high magnetic field regime where spin and valley degeneracies are fully lifted, Landau-level (LL) crossings between the top and bottom layers produce equal-sized checkerboard patterns (Fig. 1a) throughout the D/B–ν space, where ν is the filling fraction of the quantum Hall effect and B is the external magnetic field applied perpendicular to the graphene plane. The authors suggest that this resulting 4 × 4 LL checkerboard functions as a quantum sensing element for low-temperature, high-field environments — up to several tens of tesla — because the size of the resistive gaps along the displacement field directly encodes the magnetic field. Specifically, B and δD scale linearly, with a slope given by the von Klitzing constant h/e2 (Fig. 1b).
Fig. 1: Schematic of the quantized checkerboard at interlayer Landau-level crossings, which holds promises as a magnetic sensor for strong fields at low temperatures.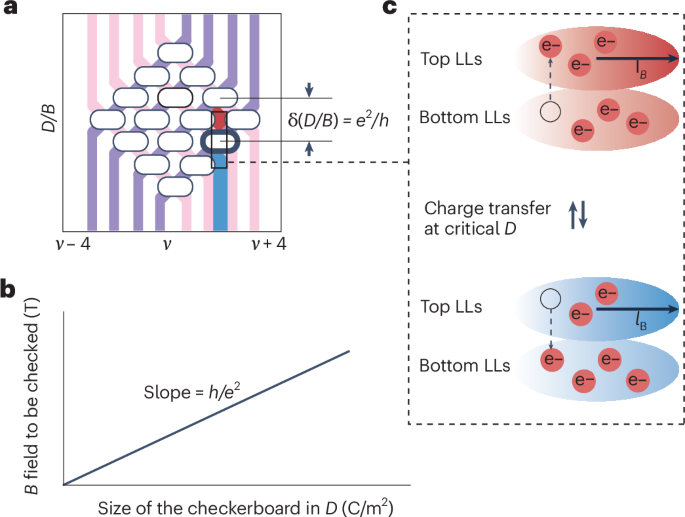
a, Landau-level (LL) crossings between top and bottom graphene layers produce equal-sized checkerboard patterns in D/B–ν space. b, B and δD scale linearly, with a slope given by the von Klitzing constant h/e2. c, In a finite vertical magnetic field, Landau cyclotron orbits start to develop in 2D electron gases. The dashed arrows indicate charge transfer. lB is the magnetic length in c.
Imagining a single electron transferred between two closely spaced two-dimensional (2D) conducting layers separated by a distance \(d\), the process follows the conventional picture of capacitive coupling under a vertically applied electric field. In this scenario, the charge transfer per area can be written as eδn = δQ = εδV/d. From the definition of the displacement field D, the carrier density change can then be expressed as
$$\updelta n=\updelta D/e.$$
(1)
Up to this point, the underlying physics appears straightforward. Nevertheless, once a finite vertical magnetic field is at play, Landau cyclotron orbits start to develop in the 2D electron gases (Fig. 1c), with the area of each Landau orbit being A = 2πlB2, where lB = \(\sqrt{\frac{\hslash }{{eB}}}\) is the magnetic length. With this constriction of LLs, the carrier density change mentioned above will also follow the relation
$$\updelta n=\updelta /A={eB}/h.$$
(2)
Combining Eqs. (1) and (2), one gets δD/B = e2/h. Specifically, the unusual electric-field-driven interlayer charge transfer of one elementary charge per flux quantum, occurring between two adjacent Landau orbits, gives rise to quantized intervals of critical displacement fields. The quantized change in the carrier density is rooted in the incompressibility of the quantum Hall insulators. Similar features have been observed in double quantum well system, but with lower resolutions8. A precisely defined spatial separation at the close limit appears to be the key. Meanwhile, the decoupled bilayer graphene (assembled with a large twist angle)7 exhibits both strong capacitive coupling, and the absence of band hybridizations between the twisted graphene layers.
It is worth noting that the above simplified picture of single-electron transfer between spatially separated Landau orbits relies on specific underlying conditions. First, for theoretical simplicity, the exchange energy is assumed to be additive across spin and valley degrees of freedom, as the long-range Coulomb interaction dominates the system. Indeed, atomic-scale interactions in graphene occur at a much smaller energy scale than the dominant SU(4)-symmetric long-range Coulomb interaction, reduced by a factor of a0/lB, where a0 is the lattice constant of monolayer graphene. For a typical magnetic length at 10 T, a0/lB ≈ 0.03 (ref. 9). Second, the reported evenly distributed checkerboard pattern may nevertheless depend on the atomic-scale interactions, since the checkerboard patterns in some samples were distorted, where these resistive states (crossing points in the 4 × 4 matrix) are divided into four sub-groups. This point is then examined by tilted-field magneto-transport of the large-angle twisted bilayer graphene sample, directly evidencing that those checkerboard pattern at LL crossings can be effectively influenced by tuning the Zeeman energy in the system.
Intriguingly, such linear magnetic field dependence of δD, scaled by the conductance quantum e2/h, can be used as a magnetometric sensor under cryogenic temperatures and high magnetic fields. That is, literally by measuring the size of the checkerboard in the space of D–n, one can immediately have the actual value of the magnetic field under test. It is known that magnetometers generally fall into two categories. Weak-field sensors (such as superconducting quantum interference devices, nitrogen–vacancy centres and fluxgates) are often engineered for fT–pT/√Hz sensitivities in near-zero background fields, and therefore typically require magnetic shielding and offer only limited dynamic range. In contrast, strong-field sensors (such as vibrating-sample magnetometers, Hall probes and nuclear magnetic resonance) are engineered for multi-tesla static or pulsed magnetic environments, prioritizing robustness and a wide dynamic range over ultimate sensitivity. In this context, the quantized checkerboard device occupies a unique niche: it offers the potential for scalable on-chip integration and micrometre-scale spatial resolution, while reliably sensing ultra-high magnetic flux densities (above 30 T) under cryogenic conditions. Interlayer charge transfer in the quantum Hall regime thus gives rise to striking physical phenomena. In large-angle twisted graphene, Landau-level crossings produce quantized checkerboard patterns, reflecting both the discrete filling fractions of the quantum Hall phase and the quantized spacing between critical displacement fields where charge is transferred. Exploiting the intrinsic relation \(\updelta D/B={e}^{2}/h\), this system can serve as a quantum-derived magnetometer, capable of sensing ultra-strong magnetic fields under cryogenic conditions, offering a rare combination of fundamental insight and potential device functionality.
