Sign up for the Starts With a Bang newsletter
Travel the universe with Dr. Ethan Siegel as he answers the biggest questions of all.
Our physical universe, to the best of our understanding, can only be made sense of because it always obeys the same fundamental laws: everywhere and at all times. It isn’t just the underlying laws of nature that apply to all physical systems, but a series of fundamental constants as well. Chief among these constants are h, Planck’s constant that governs quantum physics, c, the speed of light in a vacuum that’s the same for all observers, and G, the gravitational constant that was introduced by Newton and that remains, even today, as an inseparable part of Einstein’s field equations in General Relativity.
Even though Newton introduced G in the late 1600s, it wasn’t until 1798 that we were first able to measure it. 200 years later, we realized that many of our claimed refinements were in error, and that our uncertainties were still quite large. Even today, in 2025, G remains one of the least well-known fundamental constants, as the current figure still has a 0.0022% uncertainty on it, while h and c are now defined exactly. Can our understanding of G be improved, and if so, how? Can going to space help? That’s what our reader Otto Krog wants to know, asking:
“Given how notoriously difficult it is to measure the gravitational constant G on Earth — with different experiments still disagreeing beyond quoted uncertainties — do you think it might ever be feasible to measure G more precisely in space?”
It’s a tough question to answer, because yes, it theoretically could be done someday, but it’s very unlikely to be done anytime soon for a variety of reasons. Let’s go through the challenges and history in measuring G, and look ahead to how going to space might help.
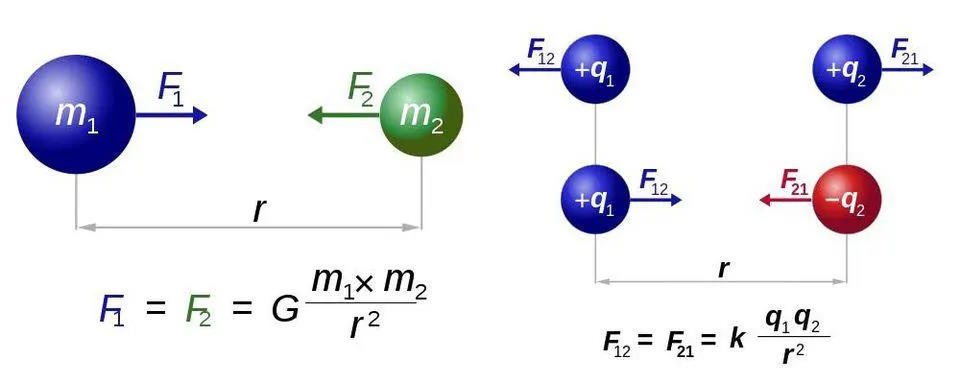
Newton’s law of universal gravitation (left) and Coulomb’s law for electrostatics (right) have almost identical forms, but the fundamental difference of one type vs. two types of charge open up a world of new possibilities for electromagnetism. In both instances, however, only one force-carrying particle, the graviton or the photon, respectively, is required.
Credits: Dennis Nilsson/RJB1, Wikimedia Commons
When Newton first came up with his law of universal gravitation, it represented a remarkable connection between the terrestrial and the celestial. Objects on Earth accelerated at the rate they did because of Earth’s gravity, the Moon orbited the Earth because of Earth’s gravity, Jupiter’s moons orbited around it because of Jupiter’s gravity, the planets all orbited the Sun because of the Sun’s gravity, etc. That one universal force of gravity — the mutual attraction of all massive objects located at any distance from one another — could explain an enormous suite of hitherto unrelated phenomena. Even Kepler’s laws of planetary motion, determined observationally, could now be derived from Newton’s law of universal gravitation.
That force law was simple:
take any two masses and multiply them together,
then divide that by the square of the distance separating those masses,
and finally, multiply that quantity by the negative of G, the universal gravitational constant,
and you’ll arrive at the strength of the (attractive) force of gravity between those two objects. But all of the examples that Newton knew to consider were based on a very large mass of some kind: the Earth, Jupiter, or the Sun, for instance. While there were many things Newton could measure or determine, G wasn’t one of them on its own; he could only determine the product of G with the larger mass in question: the G times the mass of the Earth, for terrestrial experiments, or G multiplied by the mass of the Sun, for planetary motion.
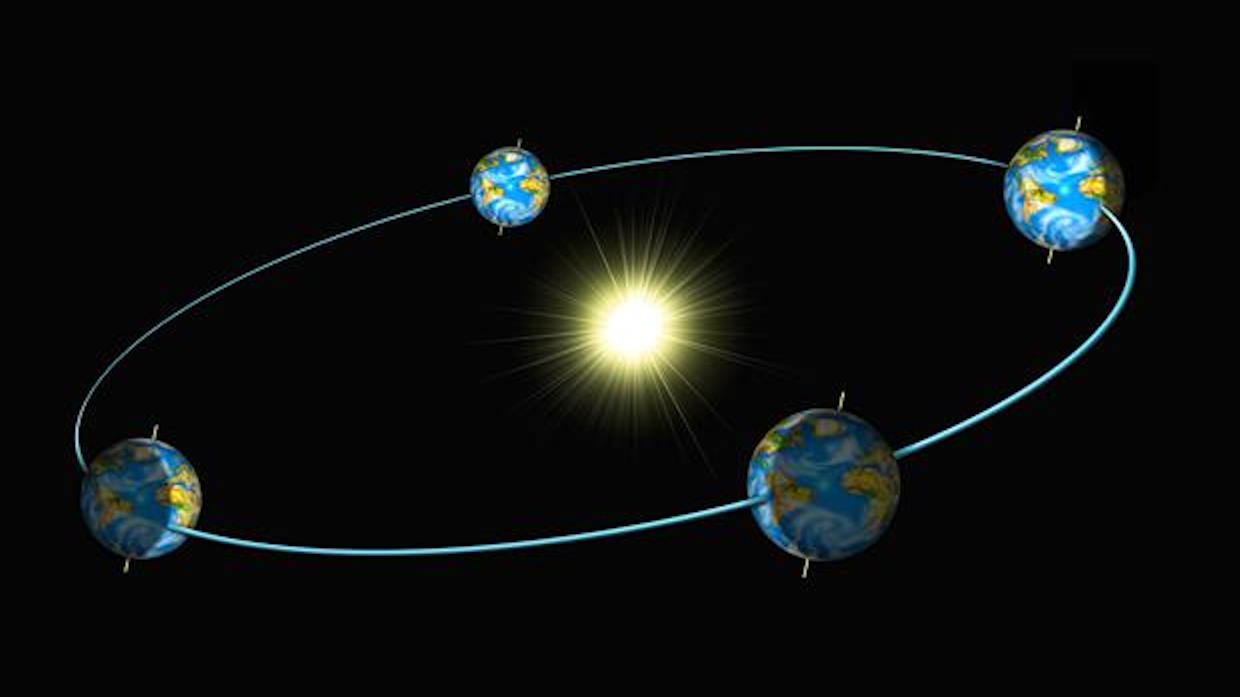
As Earth orbits around the Sun, it rotates on its axis. Although the speed of Earth’s motion is slow compared to the speed of light, moving at just 30 km/s in orbit, or 0.01% the speed of light, it’s much faster than the rotational speed, which maxes out at the equator at a much more modest 1670 km/hr (0.47 km/s). Although it’s easy to compute the laws and equations of motions for the Earth-Sun system, for example, this doesn’t provide sufficient information to arrive at a value for G, the universal gravitational constant.
Credit: Sophie DesRosiers/Montréal Space for Life
Sure, you could make crude approximations for the mass of the Earth by doing something like taking an Earth rock, measuring its density and then calculating the volume of the Earth to obtain Earth’s total mass. This method, however, is disastrous for those looking for both precision and accuracy, as it underestimates the Earth’s mass by more than 50%. (The Earth’s core and mantle, as we now know, are far denser than the crustal rocks found at the planet’s surface.) What you’d really want to do, if you were interested in separating the product of G with any mass, is to devise a way to measure one independently of the other. If you could do that, not only could you know what G is, but you could also know the mass of the Earth, of the Sun, and of any celestial body possessing orbiting satellites.
How could we do this?
The method for making such a measurement was devised not by Newton nor by Cavendish (for whom the key experiment is named), but by Cavendish’s former advisor: John Michell. John Michell was a polymath in many ways, and was the first person to theorize the existence of black holes: objects so massive in such a small volume of space that not even light could escape from it. However, Michell also devised a method for measuring G independently of any mass in the Universe, designing and constructing an apparatus known as a torsion balance back in 1783. (Yes, the first torsion balance was invented back in 1777 by Charles Coulomb, of Coulomb’s law fame, but Michell’s invention was completely independent of Coulomb’s work.)
The way a torsion balance would work is as follows.
You’d construct a stable, horizontal beam high off of the ground.
You’d protect the beam from air currents by housing it inside of a closed box.
Then, from the beam, you’d hang two small, spherical weights that were supported by a fine torsion wire in the center.
And then, you’d attach two large weights that was attached to a separate, fixed suspension.
Finally, you’d allow the small weights to be attracted to the larger weights, where the beam would rotate slightly and the torsion wire would slightly deflect, on account of the gravitational attraction between the masses.
This was Michell’s design, begun in 1783, but it remained unfinished upon his death 10 years later, in 1793.
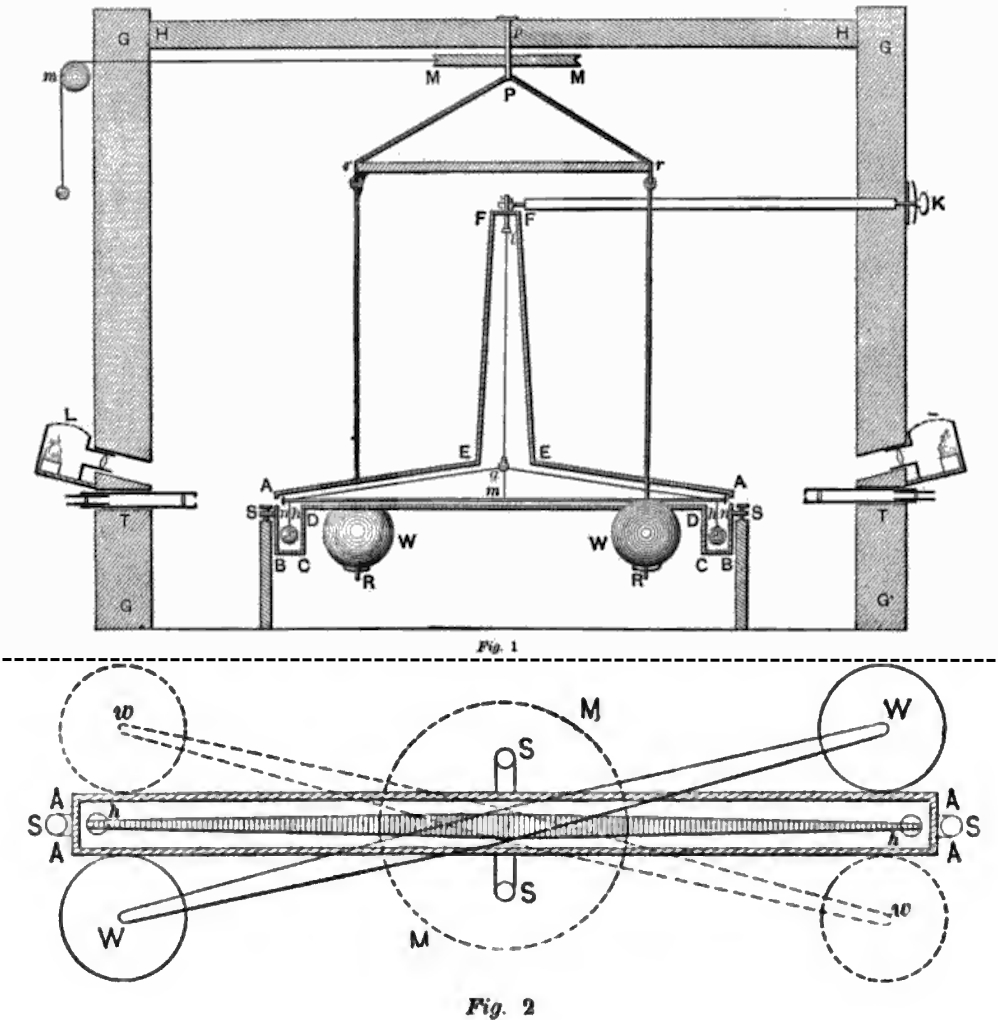
These two figures show a face-on view (top) and top-down view (bottom) of the Cavendish experiment, as illustrated by Henry Cavendish himself back in 1798. The large and small masses, the torsion balance, and the horizontal wooden beam supporting the experimental apparatus can all be easily identified here.
Credit: Henry Cavendish/public domain
After Michell’s death, the apparatus went to Francis Wollaston, before finding its way into the hands of Henry Cavendish: a scientist already famous for his discovery of hydrogen. Cavendish rebuilt and completed the torsion balance, adhering closely to Michell’s original designs, and using two large, 12-inch (0.3 meter) diameter lead balls, each weighing 348 pounds (158 kg) as the large weights. The torsion balance rod did deflect only by a super tiny amount: 0.16″ with a normal suspending wire and just 0.03″ with a stiffer suspending wire. Cavendish completed construction of this apparatus in 1797, and completed his research and published the results in 1798.
The results of the Cavendish experiment allowed him to perform some vital calculations. The angle of the rod and a knowledge of the torque of the wire leads to a determination of the forces between the pair of masses. Because Cavendish also knew the gravitational force of the Earth on the various parts of the apparatus, the ratio of those two forces would allow him to calculate the total mass of the Earth.
Cavendish could then use the mass of the Earth, because he knew the planet’s volume, to calculate the density of the Earth. Although Cavendish did make an error that wouldn’t be corrected until 1821, his value of 5.480±0.038 grams-per-cubic centimeter represented the first measurement of Earth’s density: about double the density of crustal rocks found at the surface. (The current best value is 5.514 grams-per-cubic centimeter.)
Although only 0.02% of Earth’s mass is in the form of water, that water is distributed not only in the oceans, in stores of continental freshwater, and in icecaps and glaciers, but in groundwater as well. According to a 2023 study, approximately 0.00016% of all of Earth’s water was rearranged, from groundwater to ocean water, from 1993-2010.
Credit: USGS
Interestingly from a historical perspective, this wasn’t translated into a formal gravitational constant until 1873: 75 years later. While Cavendish was interested in “weighing the world,” as he put it, the idea of calculating the gravitational constant was of great interest by the late 1800s. Using the corrected value for Cavendish’s density of the Earth, as expressed in modern units (meters cubed per kilogram per second squared), was that G = 6.74 × 10-11, which differs from the modern value by a mere 1%.
And that’s because Cavendish leveraged a key aspect of gravitation: the fact that it occurs between all objects that possess mass/energy. It doesn’t matter that we’re on the Earth, it doesn’t matter what Earth’s gravity actually is, and it doesn’t matter how large or massive or what the composition of Cavendish’s masses were. All that matters is the fact that we had masses attracting masses at a short distance, and that attraction led to a gravitational force whose effects were measurable.
Over the subsequent years, decades, and even centuries, as it’s now a full 227 years after Cavendish first published his results on “weighing the Earth,” we’ve done our best to refine our measurements of G to greater and greater precisions.
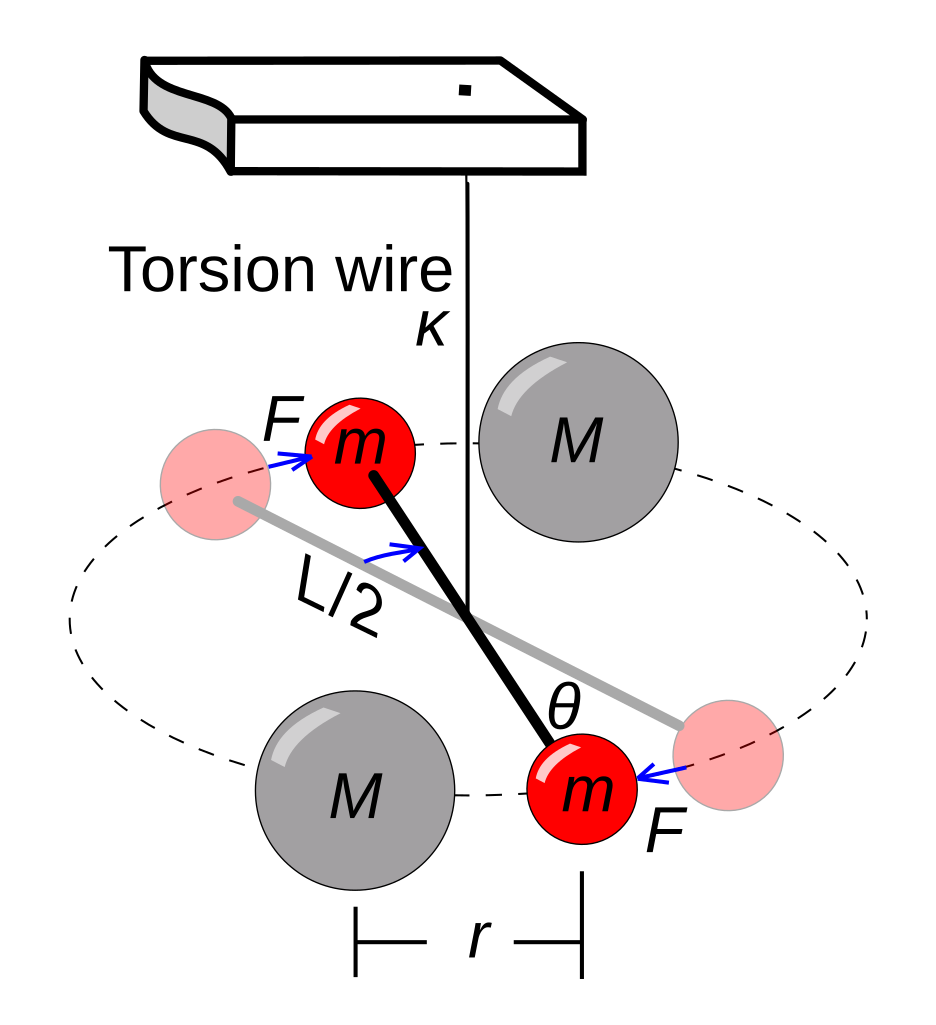
This diagram shows a torsion balance experiment similar to the one used by Cavendish (and later scientists) in attempts to measure the gravitational constant directly. The large masses (M) attract the small movable masses (m), which in turn cause the torsion wire to deflect from their equilibrium position in the absence of those masses.
Credit: Chris Burks (Chetvorno)/Wikimedia Commons
Similar attempts to measure either the mass of Earth (or, correspondingly, the gravitational constant) were conducted via pendulum experiments, but the results were less reliable than via Cavendish’s method. The first improvement came from John Henry Poynting in 1891, who measured a value of Earth’s density (and, hence, G) that differed only by 0.2% from the modern value. In 1894, Charles Boys introduced the gravitational constant, G, in the notation we still use today, and although there were many attempts to improve on Poynting’s precise results, only with the arrival of the 1930s and 1940s and the painstaking work of Paul Heyl did the errors in G finally get down to the sub-0.1% level, or fewer than 1000 parts-per-million.
Again, for all of these post-Cavendish measurements, the torsion balance method was by far the most successful one at measuring G. Other attempts have been made throughout history, such as:
by leveraging pendula and their deflection due to nearby masses,
using beam-balance scales, which can be sensitive to not only masses resting on the scale but the external influence of gravitational sources,
and through atom interferometry, a technique first successfully leveraged in 2014,
with varying degrees of success. In the latter half of the 20th century, it appeared that physicists were getting more and more precise measurements of G, with quoted uncertainties falling as low as 120 parts-per-million or even less in the 1980s and 1990s. But then, in 1998, a new, independent measurement of G came out, and it turned out to be a full 0.1% higher than those precise figures so often published in the late 20th century.
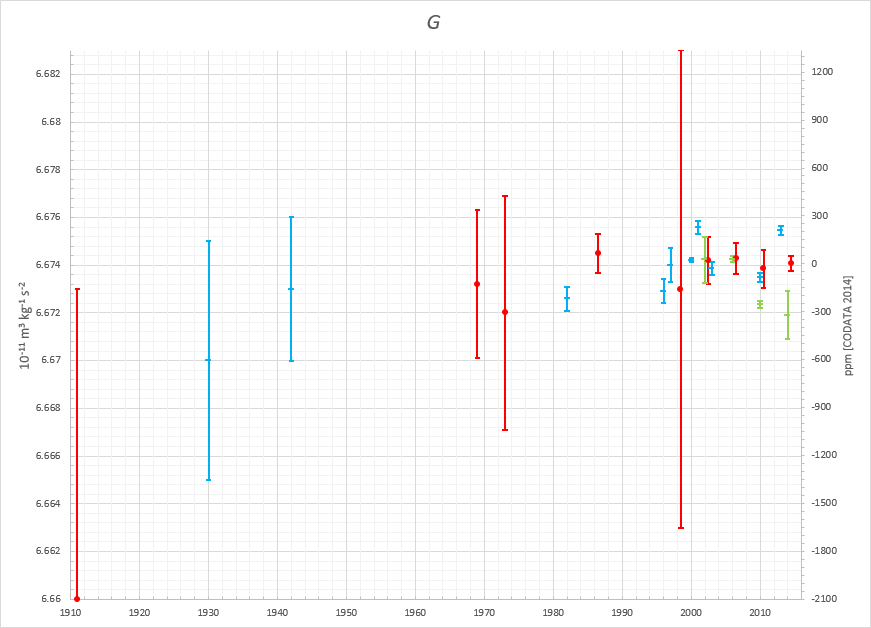
This graph shows the evolution in our best measurements of G, the gravitational constant, as a function of time. The sizes of the error bars have been variously small and large, and many of the 1980s and 1990s “consensus” measurements (that had small error bars and low values) are omitted here. A new experiment in 1998, with large error bars as shown, helped bring about our modern measurements of G. Red points are recommended values based on meta-studies; blue points are torsion balance experiment results; green points represent values from other methods, including pendula, beam balances, and atom interferometry.
Credit: Dbachmann/Wikimedia Commons
While the preferred value throughout most of the 1990s was that G = 6.67256 × 10-11 or so (again, in units of meters cubed per kilogram per second squared), that independent method instead favored G = 6.674 × 10-11, which was substantially higher than the prior consensus figures. (And hence provides the reason why, in the graph above, an enormous error bar appears in red in about 1998.) Today, our best measurements indicate that the best value of the gravitational constant is G = 6.6743 × 10-11, with an uncertainty of 0.0022% (or about 0.00015 × 10-11) on that figure.
22 parts-per-million would be a great advance to someone like Cavendish, but when you consider that many fundamental constants (like the fine-structure constant, α) are known to better than one part-per-billion, these uncertainties are actually tremendous for our modern times. In August of 2018, a new group using two independent methods published results from the world’s most accurate torsion balance experiment of all time, obtaining two excellent but mutually incompatible values for the gravitational constant of
G = 6.674484× 10-11 and
G = 6.674184 × 10-11,
each with an uncertainty of just 0.000078 × 10-11 (or 12 parts-per-million) on them. Although type Ia supernova data has established that G hasn’t varied over cosmic time by more than 1-part-in-10-billion over the past 9 billion years, we still have a long way to go to pin down the exact value of G to our desired precision.

The equivalence principle holds that there should be no difference between a gravitational acceleration and an acceleration due to any other force in the Universe. Since one is dependent on the gravitational constant and the other is not, testing the equivalence principle is a way to constrain time variations in the gravitational constant. To date, the most precise test of this principle was accomplished by the MICROSCOPE satellite: demonstrating gravitational and inertial mass equivalence to 1 part in 10^15. Measuring the gravitational constant absolutely, however, is a more challenging task.
Credit: APS/Carin Cain
Obviously, there are sources of error, uncertainty, and noise here on Earth. It stands to reason that, by going to space, we’d have a few potential advantages.
You could perform an experiment based on simple harmonic motion where an external mass attracts a ball that’s set in motion to roll within a sphere.
You could follow the lead of the proposed Project SEE (Satellite Energy Exchange), seeking to test the equivalence principle, composition dependencies of gravity, seeking inverse-square law violations, and G of course, by measuring gravitational effects on the scale of meters (within a satellite) and at distances around the radius of the Earth, projecting an error on G of under one part-per-million.
Or, in the most ambitious proposal so far, you could even leave the bounds of Earth entirely and design a deep space experiment to measure G, which would leverage harmonic motion and laser ranging to potentially improve our knowledge of G to under 100 parts-per-billion.
In theory, all of these are achievable goals. But in practice, there’s a tremendous set of difficulties that come into play. One has to do with the stability of the system and a precise, quiet knowledge of the initial conditions. For the deep space experiment, for example, the authors warn, “significant engineering advances in the release mechanism of the apparatus from the host spacecraft will likely be necessary,” pointing out just how challenging it is to achieve stable conditions.
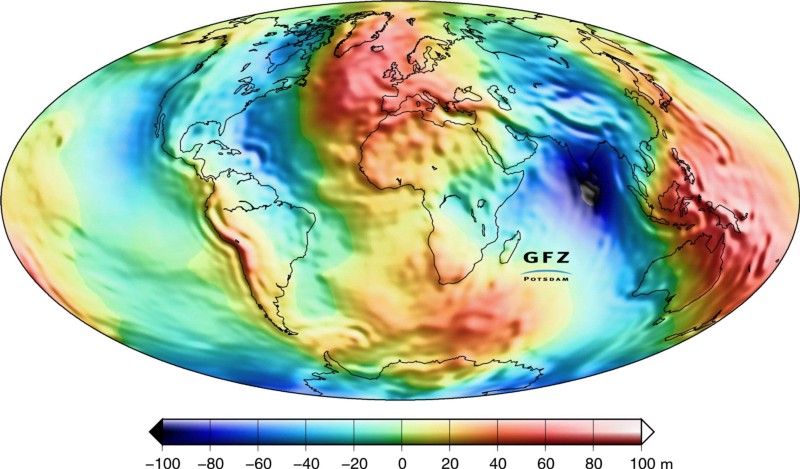
The gravitational field on Earth varies not only with latitude, but also with altitude and in other ways, particularly due to crustal thickness and the fact that the Earth’s crust effectively floats atop the mantle. As a result, the gravitational acceleration varies by a few tenths of a percent across Earth’s surface.
Credit: C. Reigber et al., Journal of Geodynamics, 2005
For experiments that are in low-Earth orbit, like the proposed Project SEE mentioned earlier, the big problem is that Earth doesn’t behave as a uniform sphere or as a point mass, but rather is a highly asymmetric object. Even if the satellite itself is exceptionally well-crafted to produce negligible gravitational forces on the measuring apparatuses inside, the problem is that masses on the Earth, as they move, can affect the internal measurements severely.
Is that gravitational effect that you see a novel gravitational effect, or is it the result of a herd of cattle in motion?
Is that a novel gravitational effect you see, or is it the result of having insufficiently precise position data?
Is that a novel gravitational effect you’re observing, or a thermal effect of the spacecraft being halfway in direct sunlight?
In fact, arrays of multiple satellites that are in orbit around Earth and are sensitive to extremely small distance differences induced between those spacecraft have been used to track how density fluctuations change in the uppermost layers of Earth’s surface. While it could have been used to track the construction of skyscrapers, the main goal of the experiment — NASA’s Gravity Recovery And Climate Experiment (GRACE) — was able to measure the seasonal movement of water across and beneath Earth’s surface. We were able to track groundwater reserves, glacial ice distribution, and even the motion of tectonic plates.

NASA’s GRACE mission consisted of two satellites in orbit around Earth. The mission lasted 15 years: from 2002-2017, and directly measured, via a variety of instruments, ice loss from Greenland and Antarctica, as well as the depletion of groundwater across the globe. It’s successor, GRACE-C, is scheduled to launch in 2028.
Credit: NASA/JPL-Caltech
But this is an accurate depiction of the problem we face. Sure, you can go to space, but if you go to the space around the Earth, you have to understand the mass distribution and how it’s changing on the Earth itself in order to measure the pure effects of gravity. In a world where freight, cargo, vehicles, equipment, livestock, and passengers are all routinely moving across Earth’s surface, this is a much more difficult task than even modern technology is up to. Performing an experiment around the Earth can better help you measure the Earth, but the same problems that plague terrestrial experiments are also going to plague low-Earth orbit experiments, with the additional burden of the enormous and increasing number of satellites present there to reckon with as well.
So it seems that going to deep space is the best bet, after all, for vastly improving our measurements of G. But you have to go quite deep:
deeper than the asteroid belt, because that changing mass distribution is not well-characterized and will have substantial effects,
deeper than the Jupiter system, because the population of Trojan asteroids poses the same problem,
and away from comets, centaurs, and any interlopers that would pass too near your spacecraft, as those gravitational effects could severely bias your results.
Additionally, the calibration issues and sources of noise aboard the spacecraft(s) sent to conduct the mission would need to be overcome as well. It’s possible, and perhaps inevitable, that in order to better measure the gravitational constant, deep space is the place to be. But the sober truth is we’re not quite ready yet; the issues to be overcome may have been identified, but the solutions to them still remain elusive.
Send in your Ask Ethan questions to startswithabang at gmail dot com!
Sign up for the Starts With a Bang newsletter
Travel the universe with Dr. Ethan Siegel as he answers the biggest questions of all.

