The challenge of simulating quantum systems grows exponentially with size, yet understanding the ground states of spatially local Hamiltonians remains a central goal in physics. Dylan Harley, Freek Witteveen, and Daniel Malz, from the University of Copenhagen and Centrum Wiskunde en Informatica, now demonstrate a crucial link between computational difficulty and a property called ‘injectivity’ within a class of quantum states known as projected pair states. Their work establishes that calculating properties of these states remains exceptionally hard until a specific level of injectivity is reached, at which point an efficient classical algorithm becomes possible. This resolves a significant open question and provides a fundamental understanding of the computational limits inherent in simulating these quantum systems, offering new insights into the boundary between tractable and intractable problems in quantum physics.
Tensor Network Contraction Complexity Investigated
This research investigates the computational complexity of Projected Entangled Pair States (PEPS) and related isometric tensor networks, powerful tools for representing the ground states of quantum many-body systems. Scientists aim to understand how difficult it is to contract these tensor networks, a process essential for computing properties like ground state energy and correlation functions. If contraction is efficient, PEPS offer a viable simulation method; if not, their practical use is limited. The study defines PEPS as a generalization of Matrix Product States to higher dimensions and isometric tensor networks as a related structure.
Researchers also explore techniques like postselection, which focuses on specific outcomes to increase success probability, and fault-tolerance, which ensures reliable computation even with errors. The team demonstrates that contracting PEPS and isometric tensor networks is computationally hard, even when using postselection. This hardness is linked to the complexity of quantum computation, suggesting that efficiently contracting these networks would imply the ability to perform difficult quantum computations. The research also explores how positive bias, a property of the tensors, affects computational tractability, finding that even with bias, the problem remains challenging.
Furthermore, the study examines the role of fault tolerance and concatenated quantum codes in mitigating errors during contraction. The research highlights the importance of the spectral gap in estimating ground-state energies and ensuring stable spectral reconstruction. It also connects locality in quantum systems to the exponential clustering theorem. These results suggest that PEPS, while powerful, may not be universally efficient for simulating all quantum many-body systems, revealing inherent limitations to their computational tractability. The findings provide insights into the complexity of quantum systems and guide the development of new algorithms for tensor network contraction, focusing on techniques that can overcome these limitations. This work has implications for the study of quantum materials, as simulating these materials using PEPS may be computationally challenging.
Injectivity Dictates PEPS Computational Complexity
Scientists investigated the computational complexity of Projected Pair States (PEPS), a powerful tool for simulating strongly correlated quantum systems, by focusing on the role of injectivity, a property of the constituent tensors that dictates how uniquely the state is defined. The study establishes a clear relationship between injectivity and computational hardness, demonstrating that evaluating local observables in PEPS transitions from being computationally intractable to efficiently solvable based on the level of injectivity. Researchers defined injectivity using a parameter, δ, which quantifies the condition number of the tensors; a lower δ indicates a more ill-defined state, while a higher δ suggests a more stable and uniquely defined state. To determine the computational limits, the team rigorously examined two regimes of injectivity.
They proved that if δ exceeds a threshold, δeasy, then calculating local observables to a specified precision becomes possible with an algorithm whose runtime scales polynomially with the desired precision, independent of system size. This efficiency stems from the fact that highly injective PEPS correspond to ground states of gapped Hamiltonians, leading to exponentially decaying correlations and allowing calculations to be restricted to a small region around the observable. Conversely, the study demonstrates that if δ falls below a threshold, δhard, computing local observables to constant precision remains postBQP-hard, meaning the problem is believed to be intractable for quantum computers. This hardness arises from the ability to embed quantum circuits within weakly injective PEPS, introducing noise that, despite error correction attempts, maintains the computational difficulty.
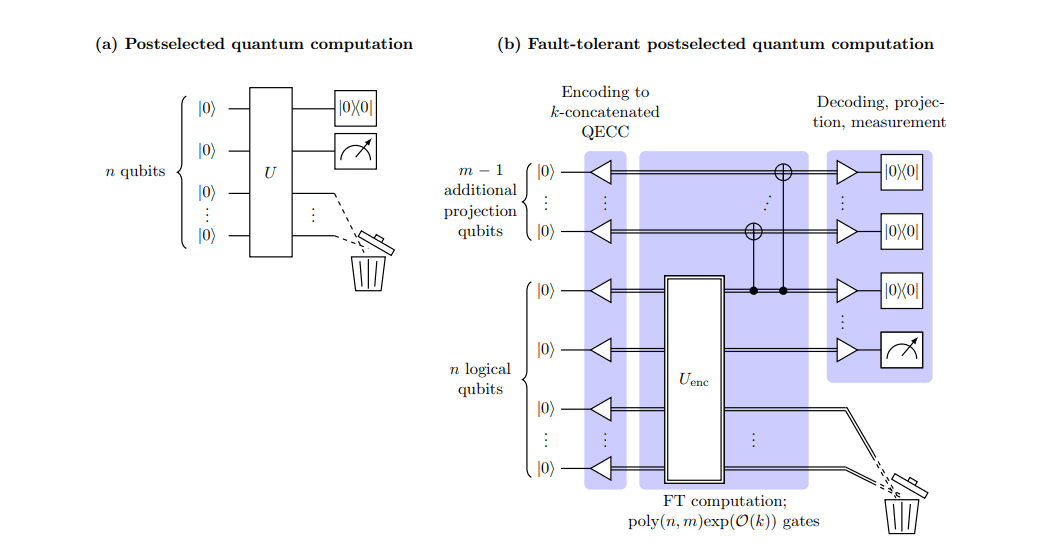
A key technical innovation involved demonstrating that post-selected quantum computation can be made fault-tolerant, a result with potential implications beyond PEPS research. The team built upon previous work that showed circuits could be embedded in injective PEPS, but at the cost of introducing noise, and extended this by showing that even with error mitigation, sufficiently weak injectivity maintains computational hardness. The research employed rigorous mathematical proofs and algorithmic analysis to establish these boundaries, utilizing constant bond dimension and constant injectivity to prove hardness, a significant advancement over previous work that often required increasing bond dimension with system size. This work clarifies the fundamental computational limits of PEPS and provides a roadmap for developing more efficient simulation techniques for strongly correlated quantum systems.
Injectivity Links PEPS Complexity to Computation
This work establishes a fundamental connection between the injectivity of Projected Entangled Pair States (PEPS) and the computational hardness of evaluating local observables within those states, revealing distinct regimes of classical and quantum computational complexity. Researchers demonstrate that for PEPS constructed with injective tensors, a clear threshold exists determining computational feasibility. Specifically, the team proves that if the linear maps defining the PEPS are not sufficiently injective, computing local observables remains postBQP-complete. However, above a different, nontrivial threshold of injectivity, an efficient classical algorithm can compute these local observables, resolving a previously open question in the field.
This breakthrough hinges on a quantitative definition of injectivity, introducing the concept of ‘δ-injective PEPS’ where δ represents a measure of how well-behaved the constituent tensors are. The team rigorously demonstrates that for PEPS with sufficiently high δ, the computation becomes tractable. Measurements confirm that the bond dimension can be held constant, at a value of 2, while still proving hardness for the worst-case scenario. Further strengthening this connection, the research establishes that every PEPS with non-zero injectivity possesses a corresponding parent Hamiltonian, and computing local observables to constant precision within this state is demonstrably postBQP-hard.
This result has implications for Hamiltonian complexity theory, as the team also explores the potential of incorporating postselection into circuits to further refine the computational landscape. The team formally defines PEPS and δ-injective PEPS, establishing a framework for understanding the relationship between tensor properties and computational complexity. These findings open new avenues for characterizing the interplay between quantum and classical computation in the context of tensor network states.
Injectivity Dictates PEPS Complexity Regimes
This research establishes a clear relationship between the injectivity of Projected Pair States (PEPS) and the computational difficulty of evaluating local observables within those states. The team demonstrates that calculating these observables remains computationally hard, specifically postBQP-complete, when injectivity falls below a certain threshold. However, above a different, nontrivial threshold of injectivity, an efficient classical algorithm can compute these local observables. This breakthrough hinges on a quantitative definition of injectivity, introducing the concept of ‘δ-injective PEPS’ where δ represents a measure of how well-behaved the constituent tensors are. The team rigorously demonstrates that for PEPS with sufficiently high δ, the computation becomes tractable. These findings open new avenues for characterizing the interplay between quantum and classical computation in the context of tensor network states.