Underwater explosion (UNDEX) has found applications in diverse research fields, including underwater mineral mining, waterway and port excavation, and warship impact and protection. The UNDEX phenomenon can be broadly divided into three distinct stages: charge detonation, shock wave propagation, and bubble pulsation1,2,3,4. The detonation stage is primarily characterized by the detonation wave generated upon ignition of the charge within its confines. This process results in the formation of high-temperature, high-pressure gas products. The discontinuity between these products and the surrounding fluid leads to the generation of a strong shock wave in the water. Subsequently, the expansion of the gas products within the water drives the bubble pulsation phenomenon. Understanding the state characteristics of the flow field behind detonation waves is a crucial prerequisite and fundamental condition for developing and refining instantaneous detonation models7,16.
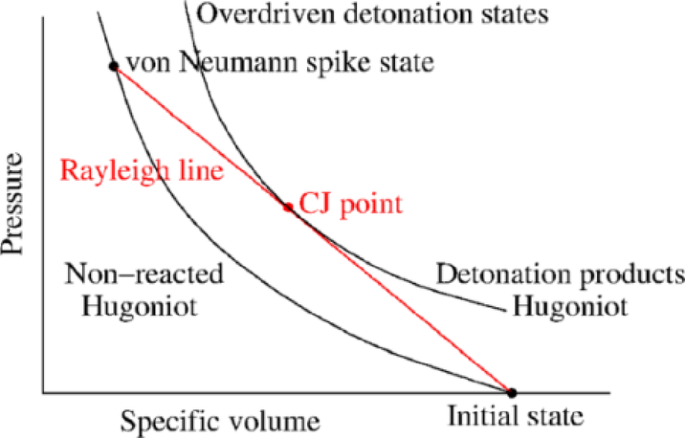
Taylor and Sedov pioneered the study of the fluid field state behind detonation waves, independently proposing the analytical solution for Chapman-Jouguet (C-J) detonation flow using self-similar theory. This solution is also known as the Sedov-Taylor solution. The nonlinear state region between the detonation wave front and the static region in the gas products is termed the Taylor wave. In a stable detonation configuration, the reaction zone is characteristically succeeded by a Taylor rarefaction wave, which effects a pressure reduction from the C-J threshold to a configuration-specific equilibrium value. As an expansion wavefront, the Taylor wave undergoes progressive spatial dilation during its propagation. In planar detonation scenarios, particle velocity exhibits approximately linear variation through the Taylor wave region, whereas pressure profiles display nonlinear decay dynamics5. The thermodynamic transformation from unreacted explosive to detonation products can be graphically represented on a pressure-specific volume diagram (see Fig. 1)6. The detonation front imparts a shock compression to the explosive, transitioning it from the initial state to the von Neumann spike condition. Subsequent pressure relaxation occurs across the reaction zone until the C-J state is attained at the sonic locus of the planar wave. Beyond this critical point, further pressure attenuation is mediated by the Taylor wave mechanism.
The diagram for the relationship between pressure and specific volume for the ZND model of detonation.
To quantitatively describe the state of the static zone and Taylor rarefaction zone, Henrych proposed that for steady detonation problems involving explosives with densities exceeding 1000 kg/m³, the state parameters behind the detonation wave of a spherical charge can be expressed as follows7:
$$\left\{ \begin{gathered} \frac{\rho }{{{\rho _D}}}={\left( {\frac{{\gamma – 1}}{\gamma }\frac{R}{{{R_D}}}+\frac{1}{\gamma }} \right)^{2/(\gamma – 1)}} \hfill \\ \frac{u}{{{u_D}}}=2\frac{R}{{{R_D}}} – 1 \hfill \\ \frac{p}{{{p_D}}}={\left( {\frac{{\gamma – 1}}{\gamma }\frac{R}{{{R_D}}}+\frac{1}{\gamma }} \right)^{2\gamma /(\gamma – 1)}} \hfill \\ \end{gathered} \right.$$
(1)
where ρ, u and p represent the density, radial velocity, and pressure within the detonation zone, while ρD, uD and pD signify the corresponding quantities at the detonation wave front. r and RD denote the interior point position and detonation wave front position. γ is the gas parameter, indicating that the gas products in the detonation zone satisfy the gamma equation. The value of γ depends on the type of explosive and is generally recommended to be between 2.54 and 3.0. For condensed explosives with densities exceeding 1000 kg/m³, the state parameters of density, velocity, and pressure on the detonation wave front can be expressed as follows:
$$\left\{ \begin{gathered} {\rho _D}=\frac{{\gamma +1}}{\gamma }{\rho _0}{\text{ }} \hfill \\ {p_D}={p_0}+\frac{{{\rho _0}{D^2}}}{{\gamma +1}} \hfill \\ {u_D}=\frac{D}{{\gamma +1}} \hfill \\ \end{gathered} \right.$$
(2)
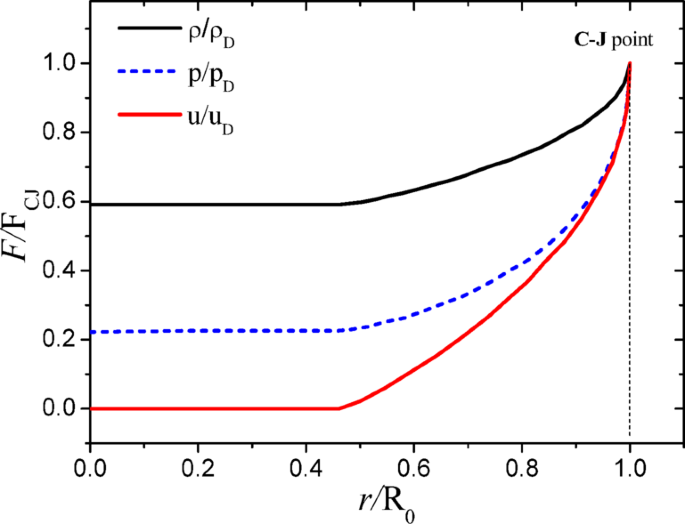
where ρ0 and p0 denote the initial density and pressure of the charge, respectively, while D represents the detonation speed. Figure 2 illustrates the distribution of density, velocity, and pressure of particles within the detonation zone following the initiation of a one-dimensional spherical TNT explosive. The parameters γ = 3 and D = 6930 m/s are employed in this analysis.
The density, velocity and pressure distribution of particles in the detonation zone after initiation of one-dimensional spherical TNT explosive.
Figure 2 shows that the particle motion in the detonation zone is similar at any time during the detonation period, and becomes the self-similarity motion. Henrych further simplifies the detonation zone to a uniform flow field. The average density, velocity and pressure of the equivalent flow field are7.
$${\rho _{eq}}=\frac{3}{4}{\rho _D}{\text{; }}{u_{eq}}=\frac{1}{4}{u_D};{\text{ }}{p_{eq}}=\frac{1}{2}{p_D}$$
(3)
The previously proposed concept of an equivalent detonation calculation model, as outlined in the preceding theory, significantly simplifies engineering calculations and has enjoyed widespread adoption. However, the model’s accuracy is limited, rendering it suitable primarily for analyzing detonation effects in far-field explosions. It is not well-suited for the precise prediction, analysis, and optimization of near-field explosions.
Jia incorporated self-similar variables into the symmetric Euler equations, thereby deriving state curves for the detonation product region under steady one-dimensional planar TNT detonation conditions, as graphically represented in Fig. 38. The state of the detonation product is characterized by the γ rate, with γ = 3 being the recommended value.
Analytical solution of self-similarity flow of detonation products in 1D plane TNT charge.
Upon comparison of Figs. 2 and 3, it becomes evident that the density and pressure within the static zone of Jia’s one-dimensional planar TNT explosive are lower than those observed in Henrych’s 1D spherical TNT explosive. Given that the detonation zone of a spherical charge explosive decays more rapidly for the same explosive type, it is reasonable to infer that the density, velocity, and pressure distribution within Jia’s 1D spherical charge zone are significantly lower than those within Henry’s. Based on the author’s investigation and experience, it is noted that no empirical formula or method equivalent to the widely recognized high-precision instantaneous detonation model has been proposed in the field of underwater explosions. Hence, there exists an urgent necessity to introduce a concise and efficient instantaneous detonation model to enhance the computational efficiency of multiphase flow in underwater explosions.