The quest to understand exotic states of matter has led researchers to explore symmetry-protected topological phases, which exhibit unusual properties arising from fundamental symmetries, and now, a team led by Hong-Yu Wang, Bao-Zong Wang, and Jian-Song Hong, all from the International Center for Quantum Materials at Peking University, reveals a new form of non-Abelian statistics within these phases. This research demonstrates that strongly correlated bosonic systems can exhibit zero modes with braiding statistics falling into two distinct classes, moving beyond the conventional behaviour expected of identical particles. The discovery is significant because these unconventional statistics, reminiscent of those found with symmetry-protected Majorana pairs, open new avenues for encoding and manipulating quantum information, potentially leading to more robust and powerful quantum computers. By focusing on a specific bosonic phase and proposing a tri-junction implementation, the team not only predicts the existence of these statistics but also outlines feasible experimental schemes and parameter regimes for achieving high-fidelity braiding, bringing the prospect of realising this exotic quantum behaviour closer to reality.
In the field of physical quantum computing, this work proposes a novel type of symmetry-protected nodal abundance (SPNA) statistics in one-dimensional strongly correlated bosonic symmetry-protected topological (SPT) phases and reveals its exotic universal features through a comprehensive investigation. Specifically, the research demonstrates that topological zero modes within these phases fall into two distinct classes of braiding statistics: one exhibiting conventional hard-core boson behaviour, and another featuring fractionalization reminiscent of non-Abelian statistics observed in other complex quantum systems.
Superconducting Qubits and Trapped Ion Research
This extensive list of references details current research in quantum computing, focusing on various platforms and techniques including superconducting qubits and trapped ions or neutral atoms. Superconducting qubits represent a leading technology, with research focused on improving coherence, scalability, and control, while trapped ions and neutral atoms offer long coherence times and high fidelity, though scaling remains a challenge. The bibliography also covers digital quantum simulation, where quantum algorithms are implemented to simulate other quantum systems, and highlights a demonstration of quantum advantage using a superconducting processor. Beyond these core areas, the bibliography covers techniques like error correction, improving quantum gate fidelity, and addressing the challenge of scalability.
Research also focuses on implementing quantum algorithms and utilizing Rydberg atoms, which have strong interactions and are used for quantum simulation and computation. Many papers explore the use of quantum computers to simulate many-body physics problems, with some hinting at the exploration of topological quantum computing concepts. The bibliography demonstrates the breadth of research being conducted in quantum computing, covering different platforms, techniques, and applications, and emphasizes practical implementation focusing on improving qubit coherence, fidelity, and scalability. It draws on expertise from physics, computer science, engineering, and materials science, and the volume of references indicates that quantum computing is a rapidly evolving field.
Symmetry-Protected Non-Abelian Statistics in Bosonic Systems
Researchers have uncovered a new form of quantum statistics, termed symmetry-protected non-Abelian (SPNA) statistics, within one-dimensional bosonic systems exhibiting strong correlations and topological protection. This discovery expands the understanding of how particles behave and interact, and opens new avenues for quantum computing. Unlike previously studied non-Abelian anyons, this SPNA statistics is inherently robust due to its reliance on fundamental symmetries. The research demonstrates that these bosonic systems, specifically those classified as symmetry-protected topological (SPT) phases, host unique zero modes at their boundaries, exhibiting exotic braiding statistics crucial for performing quantum computations.
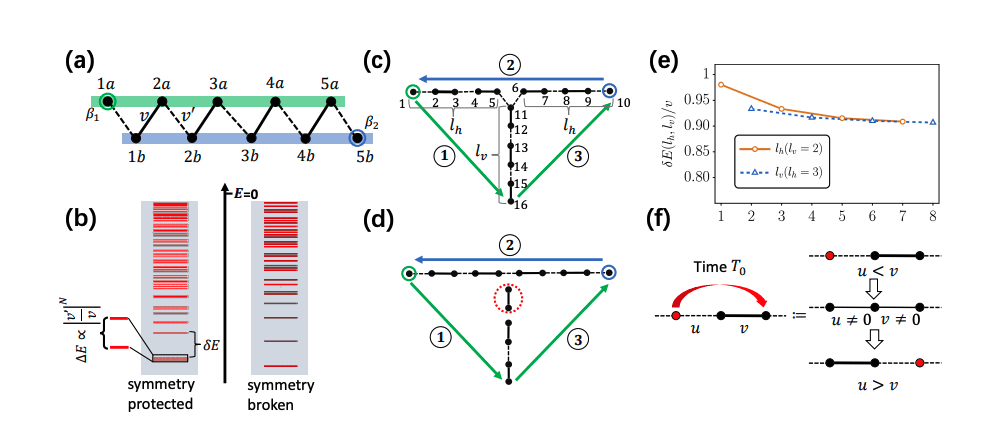
The team identified two distinct classes of braiding statistics, one resembling conventional behaviour and another exhibiting fractionalization, a splitting of quantum properties, representing a novel category of SPNA statistics. This fractionalization arises from the strong correlations within the bosonic system and distinguishes it from previously known forms of quantum statistics. The team proposes a practical method for realizing and manipulating these SPNA statistics using a tri-junction configuration within the bosonic SPT phase, allowing for the controlled braiding of the zero modes and effectively encoding and manipulating quantum information. Numerical simulations confirm the theoretical predictions, demonstrating the feasibility of implementing logical qubits and performing both single- and two-qubit gates. The robustness of this SPNA statistics offers a significant advantage over other approaches, potentially paving the way for more stable and reliable quantum computers, and extends the concept to strongly correlated systems beyond previously studied free fermion systems.
Braiding Statistics and Reflection Symmetry Revealed
This research introduces a new understanding of symmetry-protected non-Abelian (SPNA) statistics, a concept with implications for advanced quantum computation and simulation. The team demonstrates the existence of two distinct classes of SPNA statistics within one-dimensional strongly correlated bosonic systems, revealing universal features independent of specific symmetries. These classes differ in their braiding behaviour, with one exhibiting conventional hard-core boson statistics and the other displaying more exotic characteristics reminiscent of symmetry-protected Majorana pairs. The researchers establish that these distinct braiding statistics arise from the classification of non-Abelian Berry phases, determined by whether the braiding process involves a reflection operation.
They demonstrate the feasibility of realizing both classes of statistics within a specifically designed tri-junction of a bosonic symmetry-protected phase, utilising controlled local defects to manipulate the system. Importantly, the zero modes within this setup are protected by unitary symmetries, ensuring robustness against dynamical symmetry breaking. Numerical results validate the theoretical predictions, and the team proposes viable experimental schemes for implementing these SPNA statistics in analog quantum simulations. Maintaining symmetry protection throughout the dynamical evolution of the zero modes is crucial for well-defined SPNA statistics, and understanding the effects of dynamical symmetry breaking is also important, as it could potentially disrupt the braiding process. Future research directions include further exploration of the parameter regimes that ensure high-fidelity braiding and investigation of the potential for encoding and manipulating logical qubits using these newly discovered SPNA statistics.