Noise presents a major obstacle to realising the potential of quantum computers, demanding effective methods to reduce errors in calculations, and researchers are now offering a promising solution. Alexander X. Miller and Micheline B. Soley, from the University of Wisconsin-Madison’s Departments of Chemistry and Physics, alongside colleagues, present a new technique called Random Inverse Depolarizing Approximation, or RIDA, which estimates and corrects for errors using randomly generated circuits. This simple, universally applicable method effectively calculates the extent of signal loss due to noise and recovers the correct result, demonstrably outperforming existing error mitigation strategies. The improved accuracy offered by RIDA promises to unlock more reliable quantum computations across diverse scientific fields, including physics and materials science.
Numerical tests indicate RIDA outperforms key benchmarks, suggestive of significant accuracy improvements for applications of quantum computing across fields including physics and chemistry. Presently, one of the key problems facing quantum information science is how to harness its potential in the face of the high error rates encountered by today’s Noisy Intermediate-Scale Quantum (NISQ) devices. Achieving reliable results requires mitigating these errors, and current error mitigation techniques often rely on assumptions about the noise model or require substantial computational resources. Therefore, a robust and efficient method for estimating and correcting errors is crucial for advancing the field and realising the promise of quantum computation.
RIDA, ZNE, and TREX Performance Comparison
This research presents a comprehensive comparison of several quantum error mitigation techniques. The study focuses on RIDA, a promising method that estimates and corrects for errors after a computation, alongside Exponential Zero-Noise Extrapolation (ZNE) combined with TREX, and a technique using only CNOT gates with quadratic extrapolation. The results consistently demonstrate that RIDA outperforms these other techniques across a range of qubit numbers and error rates, achieving lower error and greater robustness. RIDA accurately estimates the probability of depolarization, the loss of quantum information due to noise, leading to more accurate error-free expectation values.
Importantly, RIDA’s performance degrades more gracefully as the number of qubits and the error rate increase, suggesting better scalability. The study also reveals that RIDA requires significantly fewer measurements, or ‘shots’, to achieve a given level of accuracy compared to exponential ZNE, particularly in situations with high error rates. The researchers validated the analytical predictions of RIDA’s performance, confirming that the predicted error aligns well with the numerical results. In contrast, exponential ZNE and the CNOT-only depolarization method exhibit limitations, including instability, sensitivity to noise, and the emergence of large errors.
The researchers observed a characteristic ‘V’ shape in the error curves for unmitigated circuits, exponential ZNE, and CNOT-only depolarization, indicating limitations in their ability to accurately model the error. The report’s comprehensive comparison, extensive numerical simulations, analytical validation, and detailed analysis strengthen its findings. The open-source implementation of RIDA facilitates further research and development. Further exploration could involve testing these techniques on larger quantum systems with more qubits, investigating their performance under different error models, and testing them on actual quantum hardware.
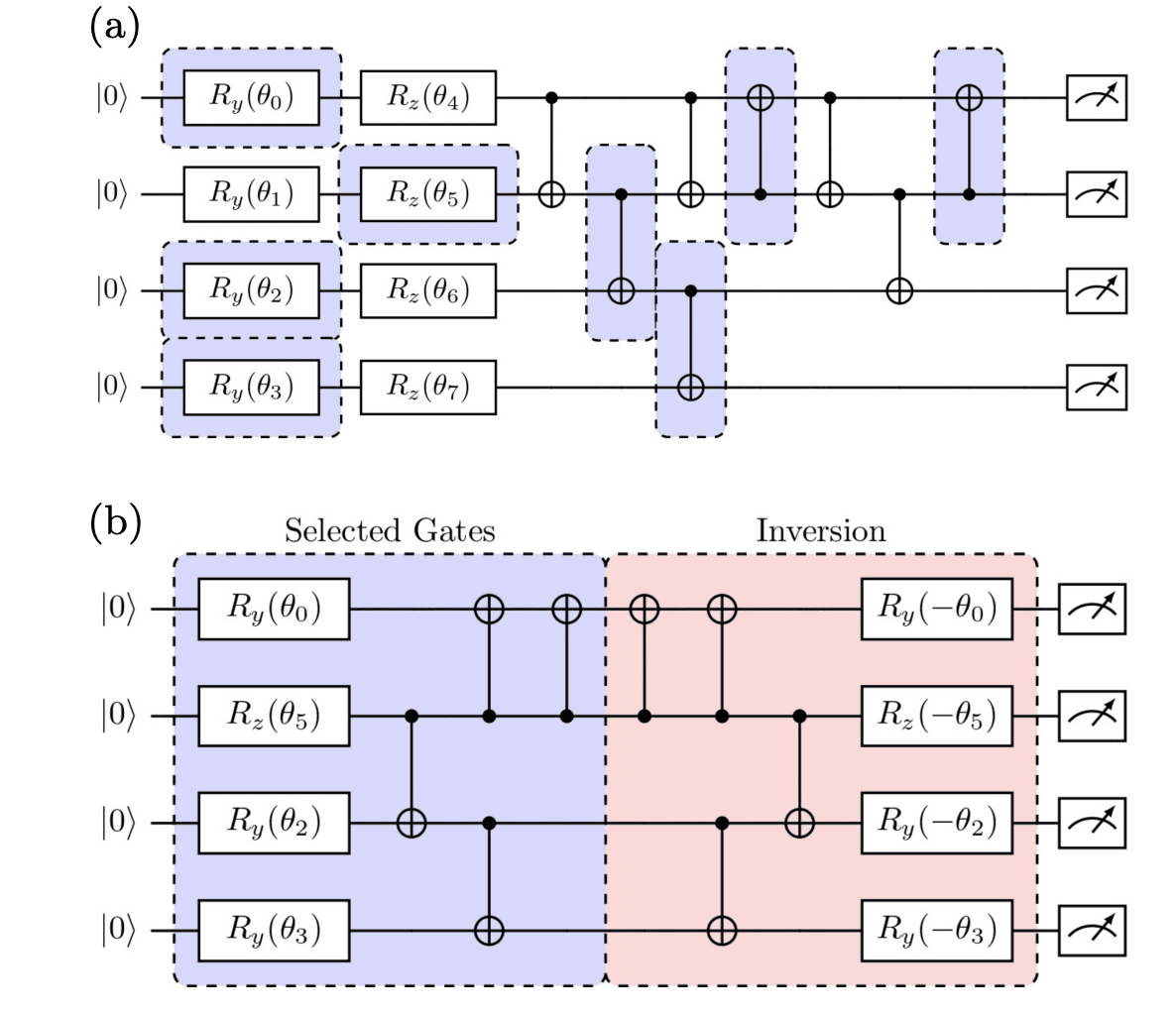
Hybrid approaches combining different error mitigation techniques could also lead to improved results. Investigating how well these techniques can characterize the underlying error sources could improve quantum control and calibration. Analyzing the computational resources required by each technique is important for practical applications, and developing adaptive error mitigation strategies that dynamically adjust parameters based on observed error rates could improve performance and efficiency. This report has significant implications for the field of quantum computing, suggesting that RIDA is a promising error mitigation technique that could enable the execution of more complex quantum algorithms on near-term quantum devices. The method addresses the critical challenge of errors that accumulate during computations, offering a pathway to more reliable results even with imperfect hardware. RIDA leverages the concept of depolarization, modeling errors as a combination of perfect quantum evolution and random noise that scrambles quantum information. The core of RIDA involves estimating the probability of depolarization using a cleverly designed estimation circuit.
Researchers randomly select half of the gates from the target circuit and combine them with their inverse, creating an estimation circuit with a known, trivial error-free expectation value. This allows for a straightforward calculation of the depolarization probability, which is then used to amplify the noisy expectation value and approximate the true, error-free result. Experiments demonstrate that RIDA consistently outperforms benchmark error mitigation techniques, including Zero-Noise Extrapolation (ZNE) and a CNOT-only depolarization method, across a range of circuit sizes, error rates, and measurement counts. This positive comparison suggests broad applicability in modern NISQ computing applications, potentially unlocking more complex and reliable quantum computations. By efficiently approximating the depolarization probability, RIDA offers a promising pathway toward mitigating errors and realizing the full potential of near-term quantum computers. RIDA estimates the overall error in a quantum circuit by using randomly generated circuits, allowing it to efficiently correct for both gate and measurement errors. Tests demonstrate that RIDA outperforms existing error mitigation methods across a range of simulated scenarios, suggesting significant potential for enhancing the accuracy of near-term quantum computers. Notably, RIDA achieves these improvements with a favourable scaling of computational resources, requiring fewer shots and gates than alternative techniques to achieve comparable accuracy. Given its promising performance, RIDA is predicted to be applicable to today’s quantum computers with up to 100 qubits, offering a practical pathway towards more reliable quantum computation.