Approaches to forecast
The simplest way to forecast is to use past values of these variables and estimate a univariate autoregressive model. In the case of the demand for health services, the forecast for each variable and for each state yields the one-step ahead forecast (see Appendix A – Eq. 1 and 2).
It is possible to augment this model by taking advantage of cross-sectional information from other states in forecasting state s’s health demand (see Appendix A – Eq. 3 and 4). This approach is consolidated practice in forecasting.
In recent times, machine learning models have also been used to generate forecasts by building up, in an iterative process, new models from the residuals of the existing models to capture complex non-linear relationships. This feature sets apart machine learning model from traditional time-series models18. The intuition behind Gradient Boosting Machines (GBM) is rooted in the idea of building on mistakes. At each stage, a weak learner is introduced to correct the errors and shortcomings of the existing ensemble. As a result, this iteration combines the predictions of multiple weak learners (individual trees) to generate a final prediction.
The combination of weak models to form a stronger ensemble is akin to the concept of Bayesian Model Averaging (BMA) in that both methods involve aggregating the predictions of multiple models. However, two alternatives are possible, and we use them both. The first one focuses on decision trees and employs a boosting approach, where each tree is trained to address the shortcomings of its predecessors, enhancing the model’s overall performance through sequential refinement.
The second approach involves combining predictions from different models using a weighted average, considering them as parallel rather than sequentially improved models. Parameters of the model are iteratively estimated by minimizing the prediction error (difference between predicted and actual values)—a procedure called gradient descent optimization technique19. In each iteration, a new decision tree is added to the ensemble, focusing on capturing the remaining errors from the combined predictions of the existing models. The model assigns weights to each tree based on its performance, allowing more accurate trees to contribute more to the final prediction. While gradient boosting is often associated with large datasets, it uses regularization techniques that are efficient in fitting non-linear relationships for small datasets20.
Using a machine learning model
We use a nonlinear machine learning model that is referred to as XGBoost (eXtreme Gradient Boostin), an implementation of gradient boosting machines (GBMs), a category of ensemble learning methods, which is efficient in handling large-scale dataset or a large number of variables. The efficiency stems from several key features. First, XGBoost employs a scalable and parallelized implementation of gradient boosting, allowing it to efficiently process and analyze massive amounts of data. It introduces regularization techniques such as L1 and L2 regularization, which mitigate overfitting and enhance generalization, crucial factors when dealing with extensive datasets. Second, XGBoost utilizes a tree-based ensemble approach, where decision trees are added sequentially to correct errors made by previous models. This not only enables the model to capture complex non-linear relationships but also facilitates the handling of a large number of variables, as it can naturally select and prioritize features. The combination of these features, along with its ability to handle missing data and provide insights into variable importance, makes XGBoost a versatile and efficient choice for a variety of tasks, especially in scenarios involving large and complex datasets.
XGBoost uses the gradient descent optimization technique to minimize an objective function
$$\hat{y}_{t} = \Sigma_{k = 1}^{K} f_{k} \left( {x_{t} } \right),f_{k} \in F$$
with respect to the model’s parameters. This approach is formalized in Eqs. 5 and 6 in Appendix A.
Gradient descent and well-established gradient methods like BFGS (Broyden-Fletcher-Goldfarb-Shanno) share the common goal of optimizing a function by iteratively adjusting parameters. However, they differ in their approaches. Gradient descent is a first-order optimization algorithm that relies solely on the first-order derivative (gradient) of the objective function. It updates parameters in the direction opposite to the gradient, aiming to minimize the function step by step. In contrast, BFGS belongs to the family of quasi-Newton methods and is a second-order optimization algorithm. It not only considers the gradient but also incorporates information about the curvature of the function through the Hessian matrix. BFGS tends to converge faster than simple gradient descent methods since it utilizes additional information about the local curvature, making it more suitable for optimizing complex and non-linear objective.
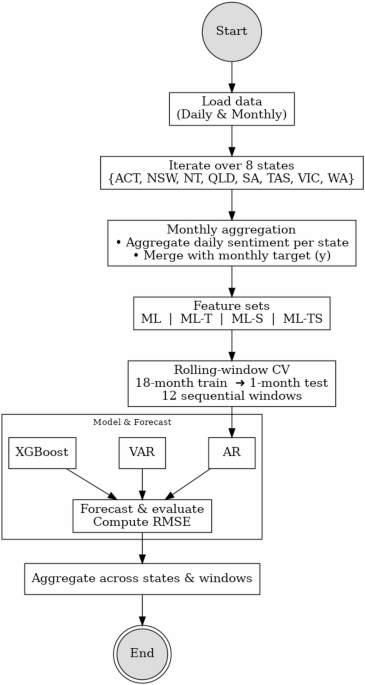
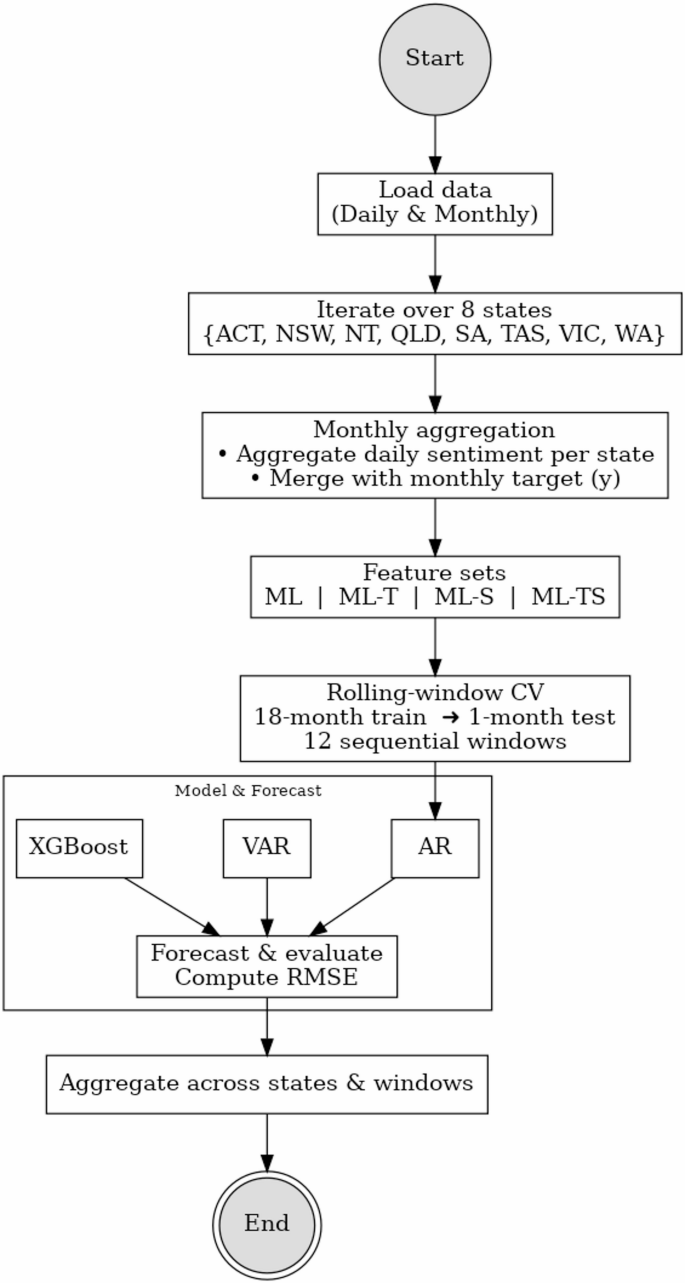
Figure 1 illustrates the full forecasting pipeline described above. The process begins with the loading of both daily and monthly data, followed by iteration across eight states and territories. Daily sentiment data are aggregated to the monthly level and merged with target variables. We then construct various feature sets with Machine learning approach (ML) and apply three forecasting models which are Autoregression (AR), Vector Autoregression (VAR), and XGBoost within a rolling-window cross-validation framework (18-month training, 1-month testing, over 12 windows). Forecast performance is evaluated using Root Mean Square Errors (RMSE) and results are aggregated across states and time windows. The details are presented in section “Results”.
Forecasting pipeline overview. Note: This flowchart outlines the end-to-end forecasting procedure used in the study. The process begins with loading daily sentiment and monthly health data, followed by state-level aggregation and feature construction.
Combining data collected at different frequencies (nowcasting)
Nowcasting model is the model to predict current events, nearby events in the past or future21,22. We applied Mixed Data Sampling (MIDAS) regression as one of common method in nowcasting model23 to utilize higher frequency data in direct predicting lower frequency data:
$$y_{t}^{s} = \beta _{0} + \beta _{1} B(L^{{1{ / }d}} ;\theta )x_{{t – h}}^{d} + \varepsilon _{t}$$
where \(B(L^{{1{ / }d}}\);\(\theta )\) is a lag polynomial that fits h-lags of the daily explanatory variable \(x_{t – h}^{d}\) as a function of a small parameter space \(\theta\) in predicting the monthly health demand \(y_{t}^{s}.\)
Therefore, we use a parametric MIDAS regression with an exponential Almon lag structure to relate daily sentiment indicators to monthly health outcomes. This structure imposes a smooth weighting across high-frequency lags using a low-dimensional parameter space. An alternative specification is the unrestricted MIDAS approach, which relaxes functional constraints on lag coefficients, enabling greater flexibility and compatibility with machine learning models. While U-MIDAS can enhance forecasting accuracy in large datasets, our approach favors parsimony and interpretability, which is important given our explanatory focus and relatively short time span of data.