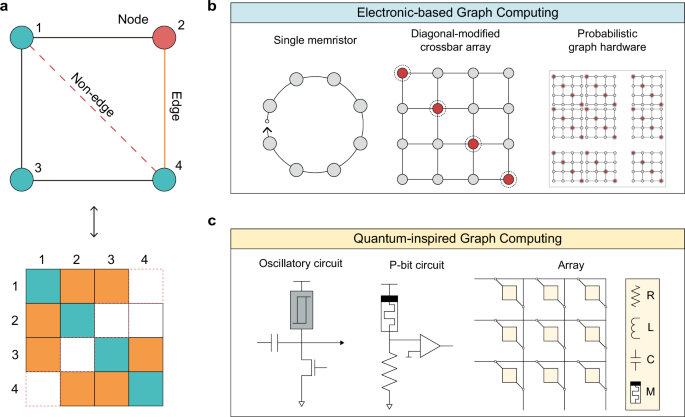
Graph computing theory
When modeling a space or circumstance in a graph, nodes represent each entity, and edges represent the relationships between the nodes. A graph \(G=(V,{E})\), which consists of \(N\) nodes \(V=\left\{{v}_{i},|,0 < i < N\right\}\) and a set of edges \(E=\left\{{e}_{{vu}},|,v,u\in V\right\}\), can be represented as an adjacency matrix \(A\in {R}^{| {N|}\times {|N|}}\). When \({e}_{{uv}}\;\ne \;{e}_{{vu}}\), \(G\) is considered a directed graph, and when a characteristic value, such as weight, \({w}_{{vu}}\) exists for \({e}_{{vu}}\), \(G\) is regarded as a weighted graph.
A graph is classified as either Euclidean or non-Euclidean based on its spatial characteristics, with distinct methodologies applied to interpret them. Each node in the Euclidean graph belongs to a metric space, situated in physical space or on a plane where Euclidean geometric concepts, such as distance and angles, are applied. For example, the graph is located on a two-dimensional coordinate plane, and the relationship between two points ((\({x}_{1}\), \({y}_{1}\)) and (\({x}_{2}\), \({y}_{2}\))) can be obtained through metric calculation, aiming to obtain the Euclidean or Manhattan distance. The distance d between two nodes satisfies the following relationships for any \(x\), \(y\), and \(z\) nodes.
$$\left\{\begin{array}{c}\left(x,y\right)=0\iff x=y\\ d(x,y)\ge 0\\ d(x,y)=d(y,x)\\ d(x,y)+d(y,z)\ge d(x,z)\end{array}\right.$$
(1)
The quantified distance implies the strength of the relationship between nodes and can be used for analyzing geographic distances.
A non-Euclidean graph is defined as one that cannot be explained using standard Euclidean geometry. Specific position vectors cannot represent any two nodes in a non-Euclidean graph. Therefore, the relationship between two nodes is abstractly expressed (for example, in a social network, the “distance” between two people refers to the degree of connection rather than actual physical distance).
Graph embedding is required to map the graph to a lower-dimensional vector space (Euclidean space) to interpret complex, high-dimensional non-Euclidean graphs more easily. In this case, the embedded graph must reflect the relationships of the original high-dimensional space as much as possible. The embedding vectors generated through the mapping function \({ENC}(v)\) must represent the local and global information that the nodes in the original graph had, which must be preserved within the embedding space61. The node \(v\) can be embedded into a lower-dimensional Euclidean vector space through the mapping function \({ENC}(v)\). Ideally, when the connection strength with a node in the original graph is high, it should be embedded close to each other. When the connection strength is low, it should be embedded farther apart.
Recently, embedding vectors have been effectively extracted using random walk-based graph embedding methods, such as DeepWalk and Node2Vec62,63. These methods do not require separate labeled data but have several inherent limitations64,65. First, they cannot reflect real-time characteristics of nodes that change over time or in response to environmental inputs. Second, the unavoidable loss of information during the graph embedding process is also a problem.
Quantum-inspired graph computing
Quantum computing employs qubits that exhibit superposition and entanglement, enabling exploration of exponentially large solution spaces. While these properties offer theoretical speed-ups over classical methods66,67, practical quantum computing remains limited by decoherence and error-correction overhead, restricting its usability for near-term, large-scale graph problems.
In this regard, QGC has emerged as a class of approaches that share conceptual elements from quantum mechanics, such as energy-based optimization and state transitions, while implementing them through classical or stochastic hardware. In QGC, problems are mapped onto graph structures, where nodes represent two-level systems and coupling edges encode their interactions. This enables hardware to directly utilize the graph’s connectivity for efficient computation, eliminating the need for coherent quantum states.
Among the approaches in QGC, probabilistic computing (p-computing) is closely aligned with quantum computing and follows similar research directions. As an intermediate between classical deterministic bits and qubits, p-bits fluctuate between 0 and 1. Various nanodevices are used for p-bit implementation, and the p-computing system is explained through the following relationships24.
$${s}_{i}={\mathrm{sign}}\left(\tanh \left(\beta {I}_{i}\right)-{\mathrm{rand}}\right)$$
(2)
$${I}_{i}=\mathop{\sum}\limits_{j}{{{\boldsymbol{W}}}}_{{ij}}{s}_{j}+{h}_{i}$$
(3)
In these relationships, the state of a two-level system si is determined by the nonlinear activation of input Ii, and inverse temperature \(\beta\), with an additional random number from [−1,1]. The input Ii to each node si (p-bit) is calculated considering the coupling matrix W and external bias field h. Here, the coupling matrix is analogous to the adjacency matrix in EGC, which explains edge interactions between the nodes. The p-computing framework is widely adopted in optimization and probabilistic inference problems24,40. Specifically, the Ising model description of the system’s energy is adopted to solve classically intractable optimization problems as follows:
$$E=-\left(\mathop{\sum}\limits_{i < j}{{{\boldsymbol{W}}}}_{{ij}}{s}_{i}{s}_{j}+\mathop{\sum}\limits_{i}{h}_{i}{s}_{i}\right)$$
(4)
Expanding upon the Ising model, other variants of QGC, such as ONN and HNN, also use graph structures to address optimization problems. Oscillatory nodes in ONN represent a multi-level system through phase difference, physically coupled according to the coupling matrix. On the other hand, HNN directly calculates the derivative of the energy (Eq. 4) to solve optimization problems. Recent studies on HNN directly map the graph to extract connectivity information56,57,58. The physical implementation of nodes and edges in quantum computing and QGC differs, as discussed in the following section, but they all physically organize graphs for efficient computation.
Advancements in structures for physical graph representation
In EGC, memristive characteristics are used to represent and interpret high-dimensional graphs without preprocessing (Fig. 2). Unlike conventional methods that require converting the graph into a vector format for interpretation (graph embedding), the goal is to represent the high-dimensional graph physically. The proposed structures commonly employ electrical signal responses to applied voltages to infer critical connectivity in graph interpretation.
Fig. 2: Hardware structures for EGC.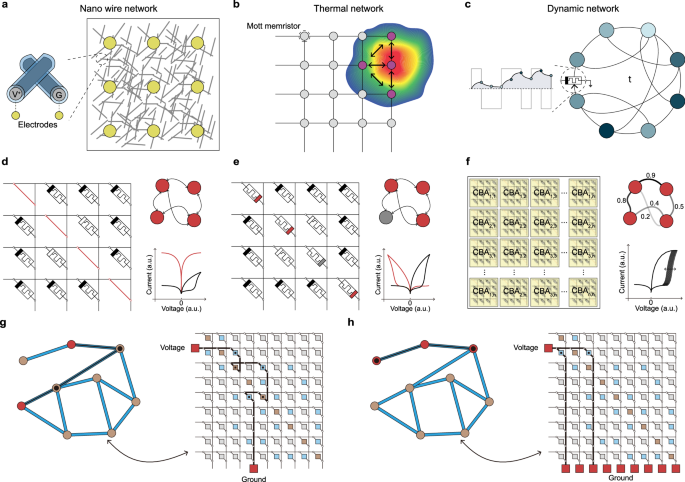
a A self-assembled metal nanowire network. Metal wires coated with ion-conductive materials are crossed, exhibiting memristive properties. Random graph dynamics arise from conductive pathways determined by the random arrangement of metal wires. b A spatiotemporal thermal conduction network based on Mott memristors. Connections between nodes are formed through thermal diffusion. c The dynamic and stochastic characteristics of memristors form a virtual circulatory network driven by applied voltage. d A CBA with a shortened diagonal. Using a self-rectifying memristor as an individual element in the array enables the physical mapping of the graph’s adjacency matrix. The right panel illustrates the represented graph and the electrical characteristics of the devices. Current flows bidirectionally through the shorted device (orange line), while it flows unidirectionally through the self-rectifying device (black line). e A CBA with a cross-wired diagonal. Similar to m-CBA, self-rectifying memristors are used as individual elements in the array. The right panel illustrates the represented graph and the electrical characteristics of the diagonal devices (orange line) and off-diagonal devices (black line). The cross-wiring configuration enables rectification along the diagonal direction, allowing for more accurate graph representation. f A module utilizing probabilistic switching devices in the diagonal shorted CBA. The right panel illustrates the probabilistic graph and the electrical characteristics of probabilistic switching devices. g, h A schematic for applying voltage to extract connectivity from the graph mapped onto the crossbar. A 9 × 9 graph can be directly mapped onto a 9 × 9 diagonal shorted CBA. The connectivity between the two nodes is determined by applying voltage and grounding to the word line and bit line of the crossbar.
For instance, nanowire graph networks are constructed in previous works8,10,11, where memristive junctions are randomly generated in self-assembled metal nanowires (Fig. 2a). The metal nanowires are electrically insulated via resistive-switching coatings (metal oxide, polyvinylpyrrolidone), and crossed wires form metal-insulator-metal junctions. When voltage is applied through additional metal pads on the nanowire graph, conductive pathways are formed within the nanowire graph, generating dynamic behavior within the random graph. This structure was used to find the shortest path in nanowire graphs, enabling applications such as associative memory. Moreover, the neuromorphic dynamics of the nanowire graph were applied in reservoir computing for data processing8,68.
Another example includes Mott memristor neuron devices (nodes of the graph), which are placed in a CBA to induce thermal conduction between them (Fig. 2b). They integrate spatiotemporal thermal information for network communication18. When the oscillation of Mott memristor neurons increases the local temperature, adjacent neurons oscillate even below their critical voltage. This thermal diffusion between neurons enables fundamental graph representation. The arrangement of neurons within the crossbar was also used to solve optimization problems such as Max-cut, providing a new perspective on graph representation through thermal conduction.
However, as the interactions between nodes are constrained by their physical positions, the structures shown in Fig. 2a, b are limited to representing grid graphs. In contrast, Fig. 2c–f shows the EGC structures capable of representing non-Euclidean graphs. Figure 2c illustrates a structure that utilizes the dynamic characteristics and inherent probabilistic behavior of a single memristor to form a complex virtual network. Appeltant et al. proposed a method to interpret a single dynamic node as a virtual cyclic graph through time multiplexing12. Guo et al. advanced this approach by utilizing the spontaneous resistance variability of memristors to implement a virtual small-world network that reflects non-uniform topological properties13. Reservoir computing using virtual graphs was demonstrated by applying time-domain inputs to memristors with such dynamic characteristics68. This method effectively generates non-Euclidean graphs by adopting the fading memory of the memristor, but its expressive capacity remains limited.
Other recent research focused on mapping the adjacency matrix of graphs to the CBAs. A two-dimensional N × N self-rectifying memristive CBA with modified diagonal components can store adjacency matrix data of a graph with N nodes14,15,16,17,21. Each (u, v) element of the adjacency matrix can be mapped based on the conductance of the memristor at uth word line (WL) and vth bit line (BL) of the CBA. The first self-rectifying memristor-based EGC hardware utilized a shorted diagonal structure14,17 (Fig. 2d). This array maps the graph by allowing reverse current flow (from BL to WL) in the diagonal devices (orange curve of Fig. 2d) while restricting current flow to the forward direction (from WL to BL) in the off-diagonal devices (black curve of Fig. 2d). Two approaches were explored to implement shorted diagonals: metal-at-diagonal CBA (m-CBA)14 and soft breakdown-at-diagonal CBA17. The latter approach offers an advantage over the former, as it allows for dynamic changes in the state of the nodes.
In another self-rectifying memristor-based EGC structure, the cross-wired CBA (cw-CBA) introduces a cross-wiring process to the conventional CBA, where the diagonal elements are connected through crossed WL and BL (Fig. 2e)15. Since the diagonal components are still composed of self-rectifying memristors, they retain the ability to modify the node states of the graph. This structure also allows the diagonal elements to flow reverse current while blocking forward current, suppressing undesired current within the array, and further enhancing the precision of graph representation15.
Research on probabilistic graph processing using probabilistic switching devices in the m-CBA was also proposed21. In this work, multiple m-CBA structures were used to implement probabilistic connectivity (Fig. 2f). When the identical adjacency matrix mapping is applied to the individual m-CBAs in Fig. 2f, probabilistic state changes occur due to device property, resulting in a probabilistic graph representation. Such a physically implemented probabilistic graph modeling system enables probabilistic graph algorithms such as steady-state estimation and PageRank69.
Moreover, methods for extracting connectivity from the self-rectifying memristor-based EGC have been proposed (Fig. 2g). The example graph contains nine nodes (left panel) and can be mapped onto a 9 × 9 shorted diagonal crossbar (right panel). To determine the connectivity between two nodes (red nodes) in the original graph, voltage and ground are applied to the WL and BL of the CBA, respectively (red boxes in Fig. 2g). Selected WL and BL correspond to the source and target node in the example graph, respectively. The amount of current output to the ground is interpreted as a measure of the node pair’s connectivity strength. This method is referred to as the single-ground method (SGM). SGM efficiently extracts information from the original graph without preprocessing. Moreover, when the ground is applied to all BLs of CBA (red boxes in Fig. 2h), a parallel circuit is formed by the devices connected to the selected WL, and information regarding the edges connected to the selected node is converted into current. The magnitude of the output current enables the estimation of the degree and 1-hop connection of the selected node. This method of quantifying the direct connectivity of individual nodes using CBA is referred to as the multi-ground method, which can be effectively used with the SGM to describe the graph’s structural characteristics.
The system needs to be designed with a structure more advanced than the peripheral circuits of conventional CBA. CBAs for high-density memory typically require random access to a single memory element. In particular, for applying CBAs in EGC, a TIA-ADC capable of current sensing in the analog domain and a multi-channel DAC structure are required for implementing a voltage scheme during the writing process. Moreover, the inclusion of a switch matrix to allow a more flexible selection of WLs and BLs should be considered.
In summary, previously reported EGC structures include nanowire8,10,11, thermal interaction, delay18, and self-rectifying memristor-based EGCs14,15,16,17,21. Nanowire and thermal interaction approaches are generally limited to grid or Euclidean graphs, while delay-based EGCs offer less flexibility in non-Euclidean graph representation (Table 1). Therefore, the following sections will focus primarily on self-rectifying memristive CBA-based approaches in further discussion of the EGC.
Table 1 Comparison of the graph representation capabilities of various EGC and QGC approaches
Figure 3 shows three different QGC structures: probabilistic computing (p-computing), ONN, and HNN. Although each structure differs in its specific design choice, they can be interpreted as graph structures with physical nodes and edges (coupling) between them. The right panels of each structure depict the implementation of nodes and edges in graphs.
Fig. 3: Hardware structures for QGC.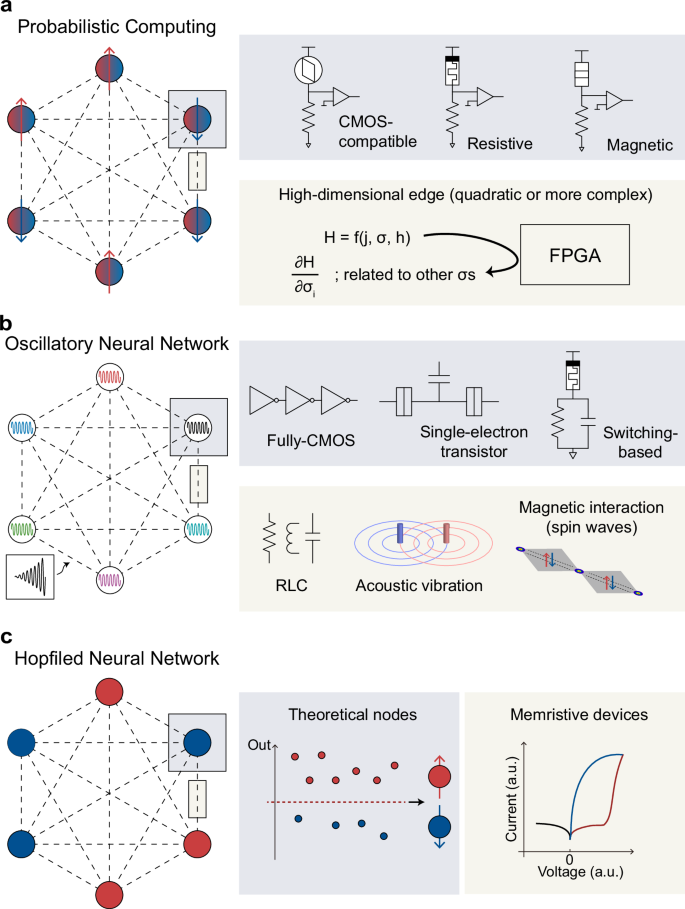
a Hardware structure for p-computing. The upper panel shows nodes of p-computing, p-bit, which are usually composed of nanodevices. b Hardware structure for ONN. Oscillatory nodes are coupled through various physical interactions. The left panel shows an injected signal for phase locking. c Hardware structure for HNN. It shows a hardware implementation based on CBA, where memristive devices are used for graph mapping.
P-computing offers a promising approach using p-bits—binary units with tunable stochasticity that mimic qubit behavior without requiring environmentally sensitive superposition (Fig. 3b)26,27. Various methods were adopted to generate p-bit, including digital complementary metal-oxide-semiconductor (CMOS) devices26,27,28,29,30,31,32, stochastic magnetic tunnel junction (MTJ)33,39, bistable resistors34, and volatile memristive devices35,36,37,38. Although their functional operations are similar, each design choice requires a different p-bit structure for nonlinear activation and thresholding. Then, these p-bits form a network in which each p-bit is interconnected with others, with the connections represented by a weight matrix W. Even though these edges encode synaptic weights between p-bits, they are usually implemented as theoretical edges and calculated in peripheral CMOS circuits such as field programmable gate arrays (FPGAs). P-computing proved efficient for logic operations and combinatorial optimization problems, as discussed in the next section.
The structures of ONN, another variant of QGC, utilize oscillator-based computing for low-power computation by using the phase and frequency of oscillation as information carriers41 (Fig. 3c). Recently, Ising machines based on ONN showed promising results in computationally demanding problems solvable in nondeterministic polynomial time. These works implemented oscillatory circuits such as CMOS ring oscillators42,46, phase-transition devices48,49,50,51, and single electron transistors53 as nodes (upper panel of Fig. 3c). Then, a network was constructed by coupling the oscillators according to the problem type. For instance, capacitive coupling of electrical oscillators tends to increase the probability of out-of-phase behavior, which can guide the system toward a stable state determined by the problem’s constraints62. Coupled oscillatory networks were also demonstrated by coupling the nodes with acoustic vibration or magnetic interaction54.
Lastly, the hardware structure of HNN, a recurrent neural network used for various optimization and content-addressable memory applications, is illustrated in Fig. 3d. The upper panel shows that a memristive CBA is employed for network mapping and parallel computation through vector-matrix multiplication55,56,57,58. Specifically, the edges of the given network are mapped to the conductance of memristive CBA, and read voltages are applied to determine the binary state of the nodes. These nodes are “theoretical” because they are not physically manifested but are defined by thresholding multiplication results. Table 1 summarizes the graph representation capabilities of the various reported QGC approaches.
Various applications of EGC and QGC
EGC offers unique advantages for implementing graph algorithms and solving real-world problems across various fields. Figure 4a–c illustrates how EGC-based graph algorithms perform compared to conventional approaches in pathfinding, link prediction, and community detection tasks.
Fig. 4: Comparison of the performance of EGC in various applications with existing models.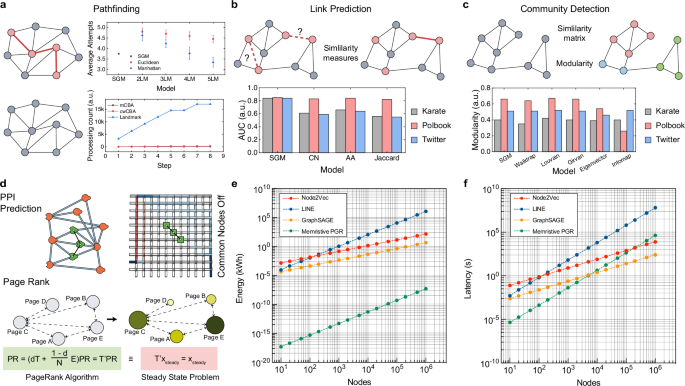
a Results of pathfinding (upper panel) and on-condition pathfinding (lower panel) using EGC and LM algorithm. In the upper panel, each symbol represents the average number of attempts, and the error bars denote the standard deviation across trials. b, c Results of link prediction and community detection using EGC and software-based algorithms. d EGC-based PPI prediction and PageRank algorithm. In the PPI network-mapped CBA, a 3-hop similarity for the PPI prediction can be achieved by deactivating the common proteins between two proteins (upper panel). The PageRank algorithm can be implemented with steady-state estimation of the EGC-based probabilistic graph. e, f Comparison of energy consumption and latency between CPU-based graph embedding and memristive PGR. The energy consumption and latency of the CPU-based graph embedding were calculated based on a single core of the Intel Core i7-10700K. The memristive PGR results were estimated based on the power and latency of the devices and peripheral circuits involved in physically mapping the graph. The graph density was fixed at 0.1 for all comparisons.
Pathfinding algorithms rely on estimating the distance from the current node to the target node. In EGC, since electrical current naturally flows along the shortest path in the graph, the inverse of the current between nodes can be used as a measure of distance. The upper panel of Fig. 4a compares the performance of the CBA-based EGC to that of traditional landmark (LM) algorithms70. In this case, a graph with nine nodes and a density of 0.3 is used to evaluate the average number of attempts required to find the shortest path. The results show that EGC’s SGM current-based pathfinding outperforms the LM algorithm when the LM algorithm uses up to four LM nodes. This outperformance results from the fact that EGC does not require graph embedding. While LM accuracy improves with the number of LM nodes, it comes at the cost of increased computational complexity and the risk of information loss during the embedding process. In contrast, EGC stores the graph structure directly in the hardware and utilizes electrical current along the shortest paths to estimate distance, providing higher accuracy and lower computational load compared to LM methods.
The lower panel of Fig. 4a presents a more complex task: on-condition pathfinding in a graph with 40 nodes and a density of 0.1, where several nodes may become unavailable during the pathfinding process (dynamic graph). In LM, every time a node becomes unavailable, the graph must be re-embedded, leading to a high processing cost. On the other hand, EGC only requires modification of the graph data stored in the CBA, making it far more suited to dynamic pathfinding. Among the EGC methods, cw-CBA is more effective than m-CBA because it allows direct modification of node states, while m-CBA requires physically turning off the edges of the unavailable node.
For link prediction tasks, which aim to forecast potential future connections between nodes, EGC offers a distinct advantage. The key to effective link prediction is the ability to evaluate multi-hop connections between nodes, typically based on their similarity71. In EGC, the SGM current between two nodes serves as a similarity measure. The lower panel of Fig. 4b compares the link prediction performance of SGM current with conventional similarity indices such as Common Neighbor72, Adamic Adar73, and Jaccard74 across three datasets14,75. In all datasets, the SGM current consistently outperforms the other models, attributed to SGM’s ability to reflect the continuous nature of graphical topology. In contrast, conventional similarity indices are discrete and may lack the resolution to distinguish subtle differences between node pairs.
Similarly, community detection algorithms, which identify clusters of nodes that are more densely connected than the rest of the graph, also benefit from EGC’s capabilities. The process typically involves creating a similarity matrix for all node pairs and merging highly connected nodes into clusters to maximize modularity76. Community detection is considered successful when the maximum modularity is high, as this reflects the quality of the identified clusters. EGC’s SGM provides a comprehensive assessment of direct and indirect connections, making it an effective similarity measure for community detection. The lower panel of Fig. 4c compares the modularity achieved by the SGM current with other algorithms across three datasets. The results show that EGC’s SGM current is comparable to the latest models, indicating that it effectively captures the high-dimensional information of the graph, while still consuming much lower computational costs.
Additionally, EGC can address real-world problems, such as protein-protein interaction (PPI) prediction or the PageRank algorithm. PPIs are fundamental to understanding the molecular mechanisms underlying various biological processes, which are essential for drug discovery and disease modeling4,77 The PPI follows the key-lock principle, where proteins with complementary structures interact selectively, requiring specialized similarity measures for accurate modeling78,79. EGC is suited for this because SGM current paths can be adjusted to match PPI characteristics (upper panel of Fig. 4d). It has been shown that SGM using EGC hardware outperforms traditional similarity measures in predicting PPIs across diverse datasets15.
The PageRank algorithm ranks nodes in a graph based on the likelihood that a random walker would land on a particular node69. PageRank is mathematically represented as a steady-state problem (lower panel of Fig. 4d). To implement PageRank with EGC, it is necessary to map probabilistic networks onto the hardware. Recent research implemented PageRank using a multiple m-CBA-based probabilistic graph21. It utilized device-to-device variations in multiple m-CBAs for probability-voltage mapping, achieving steady-state estimation with reduced time complexity.
Building on EGC’s demonstrated high performance across various tasks, its advantages extend beyond accuracy to include significant hardware efficiency. One area where this is particularly evident is graph embedding, a notoriously resource-intensive process on conventional CPU-based hardware64. As graph sizes increase, the energy consumption and latency required for embedding grow substantially. Figure 4e, f compares the energy consumption and latency of various graph embedding algorithms63,80,81 implemented on CPU hardware with the memristive PGR approach. By simplifying the embedding process, the memristive PGR method achieves not only superior energy efficiency, far surpassing traditional CPU-based algorithms, but also competitive latency performance, especially for graphs with fewer than 5000 nodes. Also, EGC offers efficient similarity computation after embedding, where the SGM retrieves node-pair similarity with a single voltage application. In contrast, conventional hardware typically relies on vector-based distance formulas, where the latency scales with the embedding dimension. While EGC latency may increase when the current path spans multiple devices due to increased R-C delay, this effect is typically minimal in real-world graphs, which tend to maintain short average path lengths owing to their small-world characteristics. When such hardware delays do occur, they can be mitigated by enhancing the on-state performance of the device, particularly by reducing resistance and ensuring Ohmic behavior.
In contrast, QGC is widely used for different applications from EGC by computing the time evolution of the networks. Figure 5 shows three representative applications of QGC. First, the invertible calculation was extensively researched using p-computing (Fig. 5a). Invertible Boolean logic and integer factorization were achieved by the energy-based representation of the problem. The right panel of Fig. 5a shows the maximum number factorized using networks of p-bits. The integer factorization of larger numbers requires complex graphs and a finely tuned annealing schedule. Subsequently, p-computing based on mature CMOS technology achieved a higher number of factorizations more effectively than emerging memories.
Fig. 5: Comparison of the performance of QGC in various applications.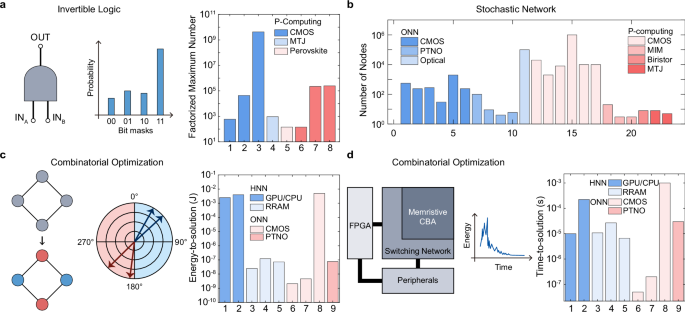
a Invertible logic of QGC. The left panel shows QGC-based invertible logic, and the right panel depicts the factorized maximum number from various structures. b The QGC-based implementation of a stochastic network and the number of nodes from different structures. c, d Combinatorial optimization using phase-based ONN (c) and iterative process in HNN (d). The right panels of (c, d) show ETS and TTS in combinatorial optimization.
ONN and p-computing are also used in stochastic network implementation (Fig. 5b). Although these methods aim for general computing purposes using network implementation, most works have focused on Ising machines for combinatorial optimization. It shows that the number of nodes in p-computing is generally larger than that of ONN due to the difficulty in the physical coupling of oscillators in ONN. Moreover, nodes based on CMOS technology, such as ring oscillator and linear-feedback shift register31,46, could achieve more complex networks than phase-transition nano-oscillators, memristors, and MTJs did33,35,48.
The third example illustrates the combinatorial optimization of QGC, further expanding the application of stochastic networks (Fig. 5c, d). The left panel of Fig. 5c shows the phase difference used for Max-Cut problem-solving through ONN, while the left panel of Fig. 5d depicts the iterative process to find the global minimum in HNN. Two qualitative parameters of energy-to-solution (ETS) and time-to-solution (TTS) are shown in the right panel of Fig. 5c, d, respectively, which refer to energy and time to obtain the global minimum in the given optimization problems. CMOS implementation59 consumes higher energy than emerging memory devices48,56,57,58. In addition, various works on ONN and HNN demonstrate TTS on the scale of nanoseconds to microseconds. However, determining the optimal approach remains challenging because the TTS is often calculated based on theoretical switching speeds or predicted clock speeds in scaled devices and is highly sensitive to the specific tuning of the algorithms employed.
Opportunities and technical challenges for future development of EGC and QGC
This section discusses the achievements and potential enhancements in device technology and integration for EGC and QGC. These improvements aim to enhance performance or broaden the scope of solvable problems for both graph computing methods.
Currently, self-rectifying memristors are predominantly used as the fundamental units for EGC (upper left panel of Fig. 6a). These self-rectifying memristors typically exhibit nonlinear current–voltage (I–V) characteristics, posing challenges for analyzing large-scale graphs. Nonlinear I–V behavior makes it difficult to extract information from graph paths with longer distances. In such cases, multiple memristors arranged in series along a graph path can cause voltage division, resulting in SGM currents that fall below measurable levels. Even when measurable, the excessively high resistance can significantly increase hardware latency. Although lower currents can enhance the energy efficiency of the CBA, the energy consumption in ADCs and DACs within peripheral circuits is much higher than that in the CBA. Therefore, decreasing latency in the CBA’s unit devices is more beneficial. To accurately capture information from distant graph paths with low latency, devices must possess rectifying and Ohmic characteristics, enabling linear I–V behavior and high current flow under specific biases, while exhibiting nonlinear I–V behavior and restricted current flow under opposite biases. This performance can be achieved by integrating a diode with a memristor with Ohmic properties (upper middle panel of Fig. 6a).
Fig. 6: Technical challenges and opportunities for future development of EGC and QGC.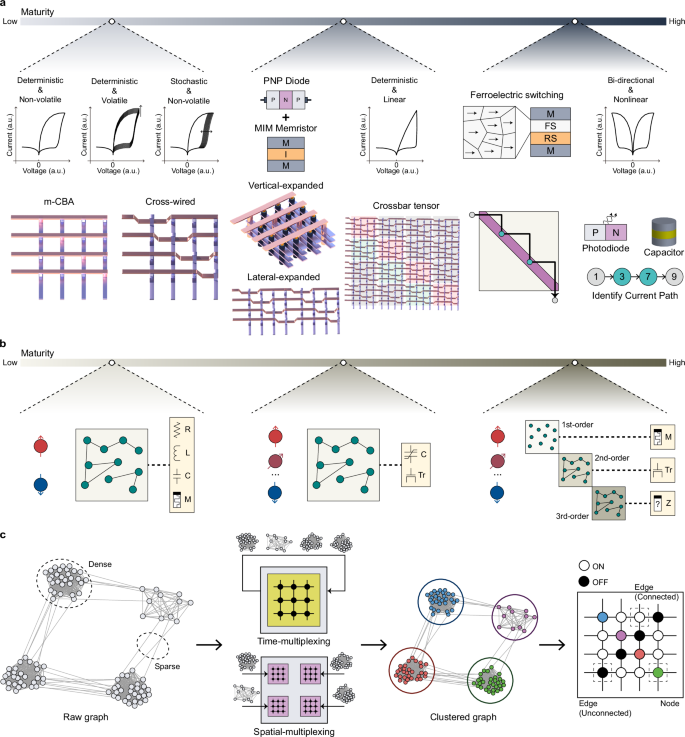
a Current and future directions for EGC. The leftmost panel illustrates the current state of EGC, showing various types of self-rectifying memristors (upper panel) integrated with CBA structures designed for planar graphs (lower panel). Progressing to the right, the figure highlights research directions to improve hardware efficiency and expand the scope of solvable problems in EGC. Developing rectifying devices with Ohmic characteristics under forward bias is required to decrease latency, along with advancements in CBA structures to support multidimensional and hierarchical graphs (middle panel). Furthermore, achieving reconfigurability in EGC hardware requires exploring devices and CBA structures capable of physically representing SGM current paths. Obtaining precise SGM current path information plays a critical role in mitigating EGC’s limitation of sequential operation. b Current and future directions for QGC. The leftmost panel depicts the current QGC, utilizing a two-level system and a low-dimensional graph. Progressing to the right, the future vision for QGC involves adopting high-dimensional, multifunctional devices to enable multi-level systems with high-order interaction edges. c Suggested clustering for EGC and QGC. A raw graph is first clustered into smaller graphs, which can be processed in a single core. After either time- or spatial multiplexing, the processed results from clustered graphs are integrated for the final output.
Furthermore, the hardware becomes reconfigurable by developing devices that manipulate rectification direction, thereby enhancing area efficiency. By allowing each device to function interchangeably as a node or an edge, processes such as metal vias or cross-wiring are unnecessary. This reconfigurability enables the same CBA hardware to represent planar, multilayer, and hierarchical graphs. Developing such devices may involve integrating ferroelectric materials, which enable polarization-based resistive switching, with memristors (upper right panel of Fig. 6a).
Also, expanding the range of solvable problems within EGC is essential. Although various graph structures exist, current EGC research is mainly limited to planar graphs (lower left panel of Fig. 6a). Representing multilayer and hierarchical graphs requires expanding CBAs laterally or vertically and utilizing crossbar tensor architectures, where multiple CBAs are arranged in a tensor structure (lower middle panel of Fig. 6a). Moreover, existing EGC hardware has only been able to verify the current value. If current path information could be obtained physically, it would enable one-shot pathfinding and applications to complex problems, such as the traveling salesperson problem. This goal could be achieved using physical elements such as light or charge. For example, incorporating light-emitting diodes at node devices would allow optical verification of current paths, or connecting parallel capacitors to node devices could enable the detection of current paths by measuring the charge on each capacitor immediately after SGM operations (lower right panel of Fig. 6a).
As discussed in Fig. 3, QGC utilizes nanomaterials to achieve high energy efficiency. As FPGA-based approaches benefit from high integration density and flexibility, QGC should utilize the massive parallelism and dynamics of nanomaterials, similar to AI accelerators19. However, QGC requires CMOS peripheral circuits, which account for most of the energy consumption and hinder achieving the theoretical switching and reading speeds. Consequently, current research focuses more on increasing the number of two-level nodes to enhance parallelism rather than improving individual devices.
Nevertheless, many real-world optimization problems require more complex nodes and interactions than the quadratic interactions of binary nodes typically handled by QGC. For example, satisfiability problems can be modeled as hypergraph problems, requiring nodes with multiple levels as the clause number increases. Furthermore, nodes interact at higher orders in these problems, which conventional QGC cannot implement without external CMOS calculations (middle panel of Fig. 6b). Recently, third-order interactions have been demonstrated by duplicating memristive devices with limited functionality55. Moreover, auxiliary nodes were used to translate a multi-level node into binary nodes for complex optimization problems in QGC40.
In the long term, the device itself should implement additional functionalities to decrease area overhead and increase integration density (right panel of Fig. 6b). For instance, three-terminal devices showed improved solution quality through continuous modulation of an additional terminal to implement adiabatic annealing60. The increased functionality will also enable parallel calculation of high-order coupling of p-computing, which was calculated in an FPGA in the previous works. In ONN, both complex nodes and edges can be realized through device engineering. The number of levels of oscillatory nodes is determined by dividing the phase into several subgroups; therefore, more precise edge coupling weights and uniform oscillations can expand the range of solvable problems using ONN. Moreover, as the edges in ONN need to correspond to those in the problem graph each time, their coupling strengths must be reconfigurable and programmable. Although electrically programmable devices, such as ferroelectric materials, are available, their practical implementation requires further development, particularly in improving the on-off ratio and endurance.
While EGC and QGC hardware have been implemented with up to tens to thousands of nodes, the ultimate goal for both hardware is to solve large-scale real-world graph problems. However, denser integration with scaled devices cannot support millions of nodes because the edge connection and coupling will increase quadratically. Consequently, full-stack research, in addition to device integration, is required.
One practical approach is clustering, which divides large graphs into manageable units by separating them into inter-cluster and intra-cluster graphs. This hierarchical analysis enables handling complex, large-scale graphs without the need for infinitely expanding hardware. It was also adopted in p-computing to realize asynchronous parallel computing42. Moreover, clustering helps address the inefficiency of mapping sparse graph data onto dense CBAs, where mapping N nodes requires an N²-sized CBA. Decreasing node numbers through clustering mitigates the discrepancy between the graph’s sparsity and the CBA’s density, enhancing area efficiency. To implement clustering-based analysis, hardware must support time-multiplexing or spatial-multiplexing operations. Achieving this would require device engineering to enable computing cores with plausible performance and architecture-level engineering to control them efficiently. Specifically, device latency and variation should be diminished to calculate on larger clustered graphs.