The steps of the improved modified extended Tanh method that were explained in the preceding section will be applied in this section to determine the exact solution for Eq. (1).
$$\begin{aligned} u(x,y,t)=z(\xi ), ~ \xi =x+y+c t. \end{aligned}$$
(7)
Substitute Eq. (7) into the original PDE Eq. (1) to obtain this ODE equation:
$$\begin{aligned} & (6+90 z) (z’)^2+(c+\sigma +6z+45z^2) z”+15(z”)^{2}+30z’z^{(3)}+z^{(4)}+15zz^{(4)}+z^{(6)}=0. \end{aligned}$$
(8)
After applying the principle of balance between the highest-order linear term \(z^{(6)}\) with nonlinear term \(zz^{(4)}\) or \(z’z”’\) in Eq. (8), we obtain \(l=2\) using the equation \((l + 6 = 2 l + 4)\). Equation (8)’s solution can therefore be expressed as follows:
$$\begin{aligned} z(\xi )=a_0+a_1 \phi (\xi )+a_2 \phi ^2(\xi )+\dfrac{b_1}{\phi (\xi )}+\dfrac{b_2}{\phi ^2(\xi )}. \end{aligned}$$
(9)
Case 1: \(d_0=d_1=d_3=0\)
Result (1)
$$\begin{aligned} a_0= & \frac{1}{15} \left( -20 d_2-1\right) ,~d_4=-\frac{a_2}{4},~a_1=b_1=b_2=0,~d_2=\frac{\sqrt{-5 c-5 \sigma +1}}{4 \sqrt{5}}.\nonumber \\ u(x,y,t)= & \frac{1}{15} \left( -\sqrt{5} \sqrt{-5 c-5 \sigma +1}+3 \sqrt{5} \sqrt{-5 c-5 \sigma +1} ~\text {sech}^2\left( \frac{1}{2} \root 4 \of {-c-\sigma +\frac{1}{5}} (c t+x+y)\right) -1\right) ,\nonumber \\ & -5 c-5 \sigma +1>0. \end{aligned}$$
(10)
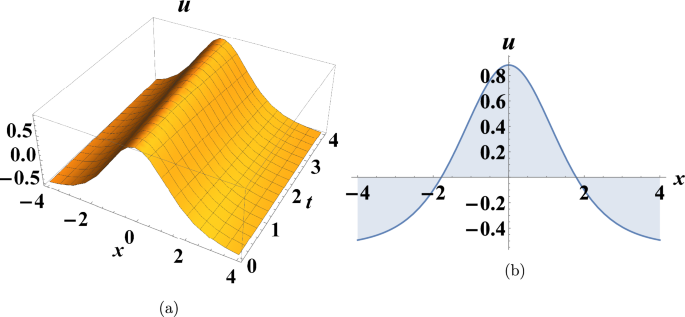
This is a representation of a bright soliton solution.
Result (2)
$$\begin{aligned} a_0= & \frac{1}{15} \left( -20 d_2-1\right) ,~d_4=-\frac{a_2}{4},~a_1=b_1=b_2=0,~d_2=-\frac{\sqrt{-5 c-5 \sigma +1}}{4 \sqrt{5}}.\nonumber \\ u(x,y,t)= & \frac{1}{15} \left( \sqrt{5} \sqrt{-5 c-5 \sigma +1}-3 \sqrt{5} \sqrt{-5 c-5 \sigma +1}~ \sec ^2\left( \frac{1}{2} \root 4 \of {-c-\sigma +\frac{1}{5}} (c t+x+y)\right) -1\right) ,\nonumber \\ & -5 c-5 \sigma +1>0. \end{aligned}$$
(11)
This is a representation of a singular periodic solution.
Case 2: \(d_1=d_3=0,~d_0=\frac{d_2^2}{4d_4}\)
Result (1)
$$\begin{aligned} a_0= & \frac{1}{15} \left( -20 d_2-1\right) ,~d_4=-\frac{a_2}{4},~a_1=b_1=b_2=0,~d_2=\frac{\sqrt{-5 c-5 \sigma +1}}{2 \sqrt{5}}.\nonumber \\ u(x,y,t)= & \frac{1}{15} \left( -2 \sqrt{5} \sqrt{-5 c-5 \sigma +1}-3 \sqrt{5} \sqrt{-5 c-5 \sigma +1} ~\tan ^2\left( \frac{1}{2} \root 4 \of {-c-\sigma +\frac{1}{5}} (c t+x+y)\right) -1\right) ,\nonumber \\ & -5 c-5 \sigma +1>0. \end{aligned}$$
(12)
This is a representation of a singular periodic solution.
Result (2)
$$\begin{aligned} a_0= & \frac{1}{15} \left( -20 d_2-1\right) ,~d_4=-\frac{a_2}{4},~a_1=b_1=b_2=0,~d_2=-\frac{\sqrt{-5 c-5 \sigma +1}}{2 \sqrt{5}}.\nonumber \\ u(x,y,t)= & \frac{1}{15} \left( 2 \sqrt{5} \sqrt{-5 c-5 \sigma +1}-3 \sqrt{5} \sqrt{-5 c-5 \sigma +1} ~\tanh ^2\left( \frac{1}{2} \root 4 \of {-c-\sigma +\frac{1}{5}} (c t+x+y)\right) -1\right) ,\nonumber \\ & -5 c-5 \sigma +1>0. \end{aligned}$$
(13)
This is a representation of a hyperbolic solution.
Result (3)
$$\begin{aligned} a_0= & \frac{1}{15} \left( -20 d_2-1\right) ,~a_1=b_1=a_2=0,~d_4=-\frac{d_2^2}{b_2},~d_2=\frac{\sqrt{-5 c-5 \sigma +1}}{2 \sqrt{5}}.\nonumber \\ u(x,y,t)= & \frac{1}{15} \left( -2 \sqrt{5} \sqrt{-5 c-5 \sigma +1}-3 \sqrt{5} \sqrt{-5 c-5 \sigma +1}~ \cot ^2\left( \frac{1}{2} \root 4 \of {-c-\sigma +\frac{1}{5}} (c t+x+y)\right) -1\right) ,\nonumber \\ & -5 c-5 \sigma +1>0. \end{aligned}$$
(14)
This is a representation of a singular periodic solution.
Result (4)
$$\begin{aligned} a_0= & \frac{1}{15} \left( -20 d_2-1\right) ,~a_1=b_1=a_2=0,~d_4=-\frac{d_2^2}{b_2},~d_2=-\frac{\sqrt{-5 c-5 \sigma +1}}{2 \sqrt{5}}.\nonumber \\ u(x,y,t)= & \frac{1}{15} \left( -2 \sqrt{5} \sqrt{-5 c-5 \sigma +1}-3 \sqrt{5} \sqrt{-5 c-5 \sigma +1}~ \coth ^2\left( \frac{1}{2} \root 4 \of {-c-\sigma +\frac{1}{5}} (c t+x+y)\right) -1\right) ,\nonumber \\ & -5 c-5 \sigma +1>0. \end{aligned}$$
(15)
This is a representation of a singular soliton solution.
Result (5)
$$\begin{aligned} a_0= & \frac{1}{15} \left( -20 d_2-1\right) ,~d_4=-\frac{a_2}{4},~b_2=-\frac{d_2^2}{d_4},~d_2=\frac{\sqrt{-5 c-5 \sigma +1}}{8 \sqrt{5}},~a_1=b_1=0.\nonumber \\ u(x,y,t)= & \frac{1}{60} \Bigg (-2 \sqrt{5} \sqrt{-5 c-5 \sigma +1}-3 \sqrt{5} \sqrt{-5 c-5 \sigma +1} ~\tan ^2\left( \frac{1}{4} \root 4 \of {-c-\sigma +\frac{1}{5}} (c t+x+y)\right) \nonumber \\ & -3 \sqrt{5} \sqrt{-5 c-5 \sigma +1}~ \cot ^2\left( \frac{1}{4} \root 4 \of {-c-\sigma +\frac{1}{5}} (c t+x+y)\right) -4\Bigg ),\quad \quad \quad -5 c-5 \sigma +1>0. \end{aligned}$$
(16)
This is a representation of a singular periodic solution.
Result (6)
$$\begin{aligned} a_0= & \frac{1}{15} \left( -20 d_2-1\right) ,~d_4=-\frac{a_2}{4},~b_2=-\frac{d_2^2}{d_4},~d_2=-\frac{\sqrt{-5 c-5 \sigma +1}}{8 \sqrt{5}},~a_1=b_1=0.\nonumber \\ u(x,y,t)= & \frac{1}{60} \Bigg (-2 \sqrt{5} \sqrt{-5 c-5 \sigma +1}-3 \sqrt{5} \sqrt{-5 c-5 \sigma +1} ~\tanh ^2\left( \frac{1}{4} \root 4 \of {-c-\sigma +\frac{1}{5}} (c t+x+y)\right) \nonumber \\ & -3 \sqrt{5} \sqrt{-5 c-5 \sigma +1} ~\coth ^2\left( \frac{1}{4} \root 4 \of {-c-\sigma +\frac{1}{5}} (c t+x+y)\right) -4\Bigg ),\quad \quad \quad -5 c-5 \sigma +1>0. \end{aligned}$$
(17)
This is a representation of a singular soliton solution.
Case (3): \(d_1=d_3=d_4=0\)
Result (1)
$$\begin{aligned} a_0= & \frac{1}{15} \left( -20 d_2-1\right) ,~a_1=b_1=a_2=0,~d_0=-\frac{b_2}{4},~d_2=\frac{\sqrt{-5 c-5 \sigma +1}}{4 \sqrt{5}}.\nonumber \\ u(x,y,t)= & \frac{1}{15} \left( -\sqrt{5} \sqrt{-5 c-5 \sigma +1}-3 \sqrt{5} \sqrt{-5 c-5 \sigma +1} ~\text {csch}^2\left( \frac{1}{2} \root 4 \of {-c-\sigma +\frac{1}{5}} (c t+x+y)\right) -1\right) ,\nonumber \\ & -5 c-5 \sigma +1>0. \end{aligned}$$
(18)
This is a representation of a singular soliton solution.
Result (2)
$$\begin{aligned} a_0= & \frac{1}{15} \left( -20 d_2-1\right) ,~a_1=b_1=a_2=0,~d_0=-\frac{b_2}{4},~d_2=-\frac{\sqrt{-5 c-5 \sigma +1}}{4 \sqrt{5}}.\nonumber \\ u(x,y,t)= & \frac{1}{15} \left( -\sqrt{5} \sqrt{-5 c-5 \sigma +1}-3 \sqrt{5} \sqrt{-5 c-5 \sigma +1}~ \csc ^2\left( \frac{1}{2} \root 4 \of {-c-\sigma +\frac{1}{5}} (c t+x+y)\right) -1\right) ,\nonumber \\ & -5 c-5 \sigma +1>0. \end{aligned}$$
(19)
This is a representation of a singular periodic solution.
Case (4): \(d_0=d_1=0\), \(d_{4}=\dfrac{d_3^2}{4d_2}\)
Result (1)
$$\begin{aligned} a_0= & \frac{1}{15} \left( -5 d_2-1\right) ,~a_2=-\frac{d_3^2}{d_2},~d_3=-\frac{a_1}{2},~d_2=\frac{\sqrt{-5 c-5 \sigma +1}}{\sqrt{5}},~b_1=b_2=0.\nonumber \\ u(x,y,t)= & \frac{1}{15} \left( 2 \sqrt{5} \sqrt{-5 c-5 \sigma +1}-3 \sqrt{5} \sqrt{-5 c-5 \sigma +1}~\tanh ^2\left( \frac{1}{2} \root 4 \of {-c-\sigma +\frac{1}{5}} (c t+x+y)\right) -1\right) ,\nonumber \\ & -5 c-5 \sigma +1>0. \end{aligned}$$
(20)
This is a representation of a hyperbolic solution.