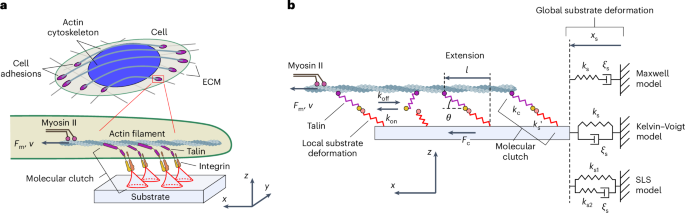
Semi-analytical mechanical model of cell-adhesion complexes
To study the potential effect of the elastic properties of molecular clutches on the mechanosensing behaviour of cell adhesion, we developed a semi-analytical theoretical framework consistent with the experimentally observed force response of molecular-clutch components at the single-molecule level22,24,25 and experimentally measured tension26,27 and force-loading rates of molecular clutches19,20. This allowed a comprehensive study of the dynamic aspects of cell-adhesion mechanics, which provided new insights into the role of different cellular elements in shaping mechanosensitive cell-adhesion behaviour.
Notably, our model can be used to describe two types of cell-adhesion complexes: talin-based and non-talin-based. In the former case, cell-adhesion complexes correspond to individual nascent adhesions (NAs) and FAs, whereas in the latter case, they represent sets of integrin clusters observed in experiments on talin-deficient cells13.
In the model, large-scale substrate deformations at the scale of cell-adhesion complexes are described using the Kelvin–Voigt model (Fig. 1b), which depicts the behaviour of elastic-like substrates with residual viscosity commonly used in experiments, such as acrylamide hydrogel and polydimethylsiloxane28,29. However, in principle, our model also allows for the incorporation of any other physical model describing substrate deformations, including the Maxwell model for liquid-like substrates (Fig. 1b) or even the more general standard linear solid model.
Furthermore, individual molecular clutches are represented in our model by two-part springs: one part describes cell adaptor proteins connecting adhesion receptors to the cytoskeleton, and the other part depicts local deformations of the substrate at the attachment sites of the adhesion receptors (Methods and Fig. 1). The elasticity of adaptor proteins is approximated either by linear springs or by a more realistic nonlinear force response described by the worm-like chain model (Methods and Supplementary Appendix F), which better reflects the experimentally observed force-induced softening of adaptor proteins, such as talin, caused by the unfolding of mechanosensitive protein domains. The local substrate deformations are related to the substrate rigidity through a spring constant, the value of which can be obtained from the theory of elasticity (equation (1) and Supplementary Appendix A).
The model distinguishes between the ‘occupied’ (‘on’) and ‘free’ (‘off’) states of sites available for the formation of molecular clutches. It quantifies the deformation of each molecular clutch under the influence of a mechanical load created by the contractile activity of myosin II motors. The dynamic behaviour of cell-adhesion complexes in the model is determined by the balance between the force generated by myosin II motors, which pulls on actin filaments within adhesion complexes, and the traction force created by mechanically stretched molecular clutches in accordance with Newton’s third law. When this balance is disturbed (due to the formation or dissociation of molecular clutches), it is restored due to the convergence of the molecular-clutch system to a stable stationary state corresponding to a steady state of the system (Extended Data Fig. 1). Thus, stable stationary states provide information about the long-term behaviour of the molecular-clutch system. By finding the probability distribution for the extension of molecular clutches in stationary states for a given substrate rigidity and knowing how the tension of molecular clutches depends on their extension, one can then calculate the total traction force created by a cell-adhesion complex resulting from the molecular-clutch-mediated transmission of the pulling force generated by myosin II motors (Fig. 1b and equation (6)). The efficiency of this force transmission, which is determined by the dynamics of molecular-clutch formation and dissociation, is a key element for understanding the mechanosensitive behaviour of cell adhesion, as can be seen from the master equation describing the time evolution of the molecular-clutch system (Supplementary equation (B10)).
A key feature of our model, revealed by exploring the model parameter space, is that it can predict diverse dynamic behaviours of cell-adhesion complexes, which are jointly determined by a number of sensitive model parameters, including the rate of molecular-clutch formation, adaptor-protein elasticity and myosin II density. As shown in Fig. 2a, three characteristic types of cell-adhesion behaviour were observed on varying the rate of molecular-clutch formation and adaptor-protein elasticity. The first was the strong cell-adhesion regime, in which cell traction increases monotonically with the substrate rigidity (Fig. 2a). This monophasic behaviour is consistent with the behaviour of wild-type (WT) fibroblast cells observed in experiments13. This regime corresponds to a high rate of molecular-clutch formation and high adaptor-protein elasticity, which buffer the tension experienced by individual molecular clutches and keep it at a low level, so that a sufficiently large number of molecular clutches can be formed to maintain strong cell traction. By contrast, when the rate of molecular-clutch formation is low and the adaptor proteins are stiff, cell traction exhibits a biphasic behaviour, increasing on soft substrates and decreasing on stiffer ones due to the shorter lifetime of molecular clutches because of their higher tension (Fig. 2a), reminiscent of the behaviour of talin-knockout (KO) fibroblasts13. Interestingly, for a certain range of adaptor-protein stiffnesses and molecular-clutch formation rates, the model predicts a bistable region in which both strong and weak cell-adhesion regimes coexist on rigid substrates. The molecular-clutch system in this case resembles the clutch of a car, where the state of strong cell adhesion corresponds to a low gear and the state of weak cell adhesion to a high gear. The bistability mode is essentially a state with a ‘rev matching’ condition that allows cells to ‘switch gear’ and change between states with strong and weak adhesion.
Fig. 2: Adaptor-protein elasticity separates molecular clutches into different groups.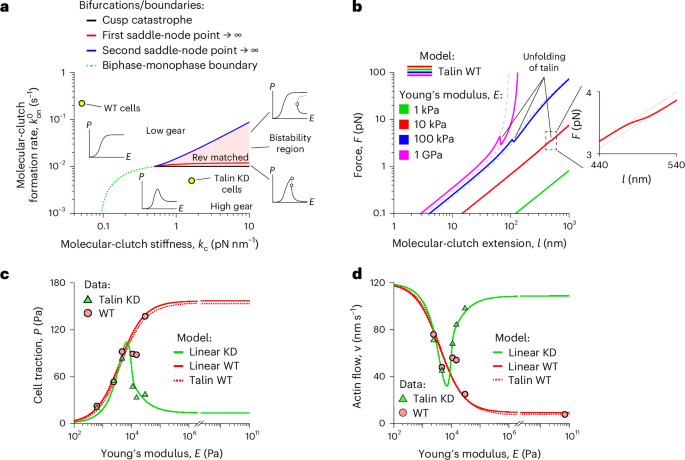
a, Stability diagram of cell-adhesion complexes. Solid curves (black, red and blue) show bifurcations that lead to the formation of a bistability region (red area) and a biphase–monophase boundary (green dotted curve), which affect the mechanosensitive behaviour of cell adhesion (‘Steady-state behaviour and bifurcation of the clutch system’). The insets around the bistability region illustrate representative cell traction curves within each domain. It is evident that increasing the stiffness of the intracellular part of molecular clutches (kc) changes the shape of the cell traction curve, shifting cells from the soft-clutch behaviour of MEF WT cells to the rigid-clutch behaviour of MEF Talin 1 KO, Talin 2 shRNA cells. b, Ensemble-averaged force–extension curves of nonlinear talin-based molecular clutches (talin WT model) for different values of Young’s modulus for the substrate (E). Dashed lines represent the force–extension curves of molecular clutches with folded and unfolded mechanosensitive R3 domains of talin at the corresponding value of Young’s modulus for the substrate. Inset: close-up of curves for 10 kPa. c,d, Fitting of experimental data for cell traction (c) and retrograde actin flow (d) from refs. 13,21 collected for MEF WT cells (red circles) and MEF Talin 1 KO, Talin 2 shRNA cells (green triangles) to the linear clutch model (linear WT and linear KD model, solid curves) and to the nonlinear talin clutch model (talin WT model, dotted curves), respectively. Both WT models reproduce the WT data, indicating that talin can be approximated as a linear spring for the substrate elasticities used in the experiment. The fitted parameter values of the linear models (Extended Data Table 2) reveal two molecular-clutch archetypes: a soft, talin-dominant one, prevalent in WT cells, and a more rigid, talin-depleted one, prevalent in talin-deficient cells.
In addition to the rate of molecular-clutch formation and adaptor-protein elasticity, these three types of cell-adhesion behaviour also depend on the densities of myosin II motors and ECM ligands, which will be discussed in more detail in the following sections. Because most of these parameters can be modulated by cells through regulating cell contractility and the composition of FAs, cells can potentially switch between the weak and strong adhesion states.
Effect of elasticity of adaptor proteins on cell adhesion
Using a few physiologically relevant fitting parameters (Extended Data Table 2), we found that our model could fit well previously published experimental data, such as retrograde actin flow and cell traction measured at different values of Young’s modulus for the substrate13,21,30 (Fig. 2c,d). This makes it possible for the model to be used to plot cell-adhesion stability diagrams and extract detailed information about molecular-clutch dynamics at the single-molecule level from experimental data obtained from cells, including the average tension and conformational changes of molecular clutches, which may provide new insights into the key factors regulating FA behaviour.
Previous single-molecule experiments showed that the mechanical responses of adaptor proteins, such as talin, are highly nonlinear and subject to force-induced softening due to the unfolding of their force-bearing protein domains. Therefore, we first investigated how the nonlinear elasticity of adaptor proteins affects the mechanosensitivity of cell adhesion. To do this, we treated the intracellular part of molecular clutches as a nonlinear spring with a force response corresponding to that of talin measured in single-molecule studies22, including the force-dependent unfolding of the mechanosensitive R3 domain of talin. See the talin WT model described in Supplementary Appendix F.
Fitting experimental data about the mechanosensitive behaviour of mouse embryonic fibroblast (MEF) WT cells from ref. 13 to the steady-state solution of the talin WT model (Fig. 2c,d) using the model-fitting parameters listed in Extended Data Table 2 revealed that even at the highest substrate stiffness, most talin-based molecular clutches experienced relatively low tension in the range 0.7–1.3 pN (Supplementary Fig. 1b). This tension was below the force level at which the nonlinear elastic properties of talin become strongly pronounced (Fig. 2b). In addition, the model predicted that on rigid substrates, only a small percentage (1–2%) of talin-based molecular clutches would be subject to forces sufficient to substantially stretch talin molecules and trigger the unfolding of their mechanosensitive domain (Supplementary Fig. 1a). This finding is in good agreement with a recent experimental study performed on Xenopus laevis cells grown on a fibronectin-coated glass substrate, in which only about ~4% of talin molecules underwent substantial conformational changes upon stretching the molecular clutch31.
These results indicate that if the elasticity of adaptor proteins has any effect on cell traction and retrograde actin flow, it is the passive linear elasticity of adaptor proteins that is important. Accordingly, the experimental data from ref. 13 could be fitted to a simplified model in which the intracellular part of molecular clutches is represented by a linear spring (the linear WT model) as accurately as the talin WT model with a more realistic nonlinear force response of the intracellular part of molecular clutches (Fig. 2c,d).
Further comparison of model parameter values obtained by fitting experimental data collected from WT and talin-depleted MEF cells to the linear molecular-clutch model confirmed that the elasticity of adaptor proteins is, indeed, one of the key factors influencing cell-adhesion behaviour. For MEF WT cells, the fitted elasticity of the intracellular parts of molecular clutches (kc = 0.05 pN nm−1) was found to be close to the elasticity of talin estimated from previous single-molecule measurements (0.09 pN nm−1; Supplementary Table 3). On the other hand, the intracellular parts of molecular clutches in MEF Talin 1 KO, Talin 2 shRNA cells were predicted to be more than ten times stiffer (kc = 1.6 pN nm−1) compared to MEF WT cells. Because previous single-molecule studies have shown that typical cytoskeletal proteins found in cell-adhesion complexes have elasticities less than 0.3 pN nm−1 (Supplementary Table 3), these data indicate that rigid molecular clutches may form through the clustering of adaptor proteins. Indeed, FA proteins such as kindlin and α-actinin have been shown to bind to FAs before talin and form clusters or condensates32,33,34. Because these proteins are also present in MEF Talin 1 KO, Talin 2 shRNA cells, they could potentially contribute to the increase in molecular-clutch rigidity predicted by the model. This result is supported by the much larger characteristic size of the adhesion site of molecular clutches in talin-KO cells (r = 26 nm) compared to WT cells (r = 0.6–0.8 nm), which was obtained by fitting experimental data (Extended Data Table 2). In the future, super-resolution microscopy could be used to test the model-predicted difference between the characteristic sizes of adhesion sites of talin-based and non-talin-based molecular clutches. Overall, our model indicates that there are two types of molecular clutches in MEF cells—soft, talin-based and rigid, non-talin-based—which are formed by clustered adaptor proteins. Indeed, a model describing the competitive formation of these two types of molecular clutches (WT-2 model; Supplementary Appendix G) was found to more closely fit the experimental data obtained from WT and talin-depleted MEF cells (Extended Data Fig. 2a,b).
Finally, a more detailed analysis of the force–extension curves of nonlinear talin-based molecular clutches at different values of Young’s modulus for the substrate (E) showed that on soft substrates (E ≤ 10 kPa), the mechanosensitive behaviour of cell adhesion is determined primarily by the elastic characteristics of the extracellular part of the molecular clutches (local substrate deformations), whereas on rigid substrates (E > 10 kPa), the elasticity of the intracellular part of the molecular clutches begins to play a more important role in this process (Fig. 2b). This result is in good agreement with the graphs presented in Extended Data Fig. 3a,b, which show that the spring constant of the intracellular part of molecular clutches (kc) affects cell behaviour only on rigid substrates, but not as much on soft ones. Thus, the elasticity of both the intracellular and extracellular parts of molecular clutches is a key factor influencing the mechanosensitive cell-adhesion behaviour on substrates with different stiffnesses. Because many adaptor proteins contain long stretches of conserved intrinsically disordered regions, such as tensin, these results imply that such flexible domains may play an important role in regulating the mechanosensitive behaviour of cell adhesion.
Ligand density affects cell adhesion through myosin II feedback
To investigate the effect of the density of molecular clutches on cell adhesion, we fitted previously published experimental data on MEF WT cells and MEF Talin 1 KO, Talin 2 shRNA cells plated on elastic substrates that were coated with different fibronectin concentrations13. Because the density of the fibronectin network affects the rate of molecular-clutch formation and the distribution of the mechanical load near adhesion sites of molecular clutches, the data were fitted by varying the clutch formation rate and the characteristic size of adhesion sites of molecular clutches. The density of myosin II motors was also varied. Using this approach, the experimental data could be fitted fairly well to the linear knockdown (KD), linear WT and talin WT models (Fig. 3a,b).
Fig. 3: Ligand density influences molecular-clutch kinetics and myosin II organization.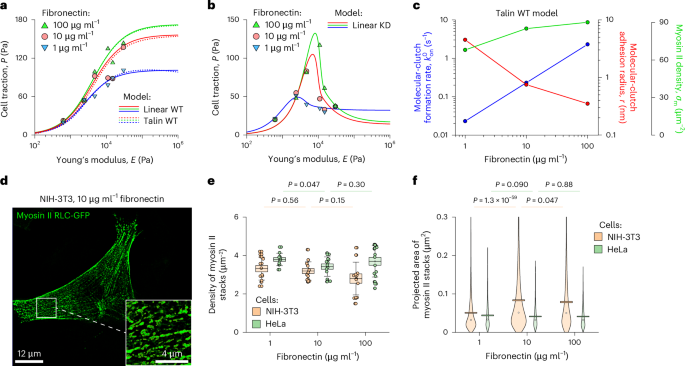
a,b, Cell traction measured on MEF WT cells (a) and MEF WT and MEF Talin 1 KO, Talin 2 shRNA cells (b) plated on substrates coated with increasing concentrations of fibronectin13. The experimental data were fitted to the talin WT model (dotted curves) and the linear WT and KD models (solid curves) by varying the rate of molecular-clutch formation (\({k}_{{\rm{on}}}^{0}\)), the characteristic size of adhesion sites of molecular clutches (r) and the density of myosin II motors (σm). Other model parameters were held fixed (Supplementary Table 1). c, The best-fitting parameter values as a function of fibronectin density show that enriching the ligand density accelerates molecular-clutch formation, reduces the characteristic size of adhesion sites of molecular clutches and increases the density of myosin II, thereby enhancing actin–substrate force transmission. d, Structured illumination microscopy image of an NIH-3T3 fibroblast expressing myosin RLC-GFP. Inset: close-up of the boxed region. e,f, Quantification of myosin II filament stacks in NIH-3T3 and HeLa cells. Increasing the fibronectin density did not alter the density of myosin II stacks (e) but did alter their projected area in a cell-type-dependent manner (f). The response of NIH-3T3 cells is consistent with model predictions for MEF WT cells. In e from left to right, N = 13, 11, 14, 13, 12 and 16 cells were processed under the corresponding experimental conditions. In f from left to right, N = 2,534, 846, 3,836, 834, 2,305 and 928 stacks of myosin II filaments were collected and processed under the corresponding experimental conditions from the same number of cells as indicated for e. Boxes and error bars in e represent mean ± standard errors of the mean (s.e.m.) and standard deviation, respectively. The circles in f show the median, and boxes represent the mean ± s.e.m. The pairwise statistical difference between the corresponding datasets was calculated using one-way ANOVA with post-hoc Tukey’s honestly significant difference test (no adjustments).
Interestingly, the fitted data showed a correlation between myosin II motor density (σm) and fibronectin concentration, as the fitting did not converge when the myosin II density was fixed. According to the model, the density of myosin II motors pulling on actin filaments decreased by ~25% on substrates coated with 1 μg ml−1 fibronectin solution compared to those coated with 100 μg ml−1 fibronectin solution (Fig. 3c). To test this model prediction, we transfected NIH-3T3 cells with the myosin regulatory light chain (RLC)-GFP35 and measured the density and the average size of stacks of myosin II filaments labelled with this construct as a function of the fibronectin concentration (Fig. 3d–f). As a control, we also performed similar measurements with HeLa cells.
We found that, although in HeLa cells myosin II motors formed more or less uniform assemblies resembling beads on a string (Supplementary Fig. 2), in NIH-3T3 cells, they formed stacks that were more irregularly shaped (Fig. 3d). More importantly, although the fibronectin concentration was found to have little effect on the density of stacks of myosin II filaments in both NIH-3T3 and HeLa cells (Fig. 3e), it had a strong effect on their average size in NIH-3T3 cells (~35% drop for a 1 μg ml−1 fibronectin solution compared to a 100 μg ml−1 solution) but not in HeLa cells (Fig. 3f), indicating that this effect may depend on cell type. Thus, the model developed in our study can accurately capture the mechanical states of fibroblast cells and make physiologically relevant predictions.
Previous studies have shown that fibronectin density can influence the activation of rho kinase (ROCK) in endothelial cells. ROCK controls the assembly of myosin II filaments36. Thus, MEF cells could potentially use a similar mechanism. However, the precise molecular pathways responsible for the fibronectin-dependent activation of ROCK remain unknown. Because our observations indicate that such a feedback loop depends on cell type, it may be possible to gain detailed insights into the origin of this phenomenon by comparing normal and transformed cells.
Vinculin modulates force-loading of molecular clutches
Having established that the model can reproduce the mechanosensitive behaviour of cell adhesion, such as traction force and retrograde actin flow, we next tested whether the model can describe the mechanical dynamics of individual molecular clutches. Recent advances in the development of tension-gauge DNA sensors have made it possible to directly measure the force-loading rate and lifetime of integrin–ECM adhesion bonds. Experimental studies have shown that individual molecular clutches can experience forces above 40 pN, whereas measured force-loading rates are in the range 0.2–4 pN s−1 (refs. 19,20). Furthermore, the force-loading rate seems to vary with the molecular-clutch tension20. For example, it takes much longer for molecular clutches to reach a tension of 7–19 pN than to subsequently achieve a tension of 19–41 pN, a phenomenon that cannot be explained by existing models in which molecular clutches are represented by linear springs, because the force-loading rate of such molecular clutches does not depend on the applied tension. In addition, Hu et al. demonstrated that vinculin plays an important role in stabilizing the tension experienced by molecular clutches, as MEF vinculin-KO cells showed an increased force-loading rate and reduced lifetime of adhesion bonds20. The latter result is counter-intuitive, as the measured maximum tension experienced by molecular clutches in MEF vinculin-KO cells was lower than that in MEF WT cells, which is in good agreement with the experimentally observed reduction in cell traction in MEF vinculin-KO cells21. Because the binding of vinculin to talin, on the one hand, stabilizes molecular clutches37,38 and, on the other hand, keeps talin in an unfolded state22 causing an increase in the elasticity of molecular clutches, we tested whether these two factors are the main ones responsible for the observed effect of vinculin on cell traction and force-loading rates of molecular clutches.
To do this, we first tested the effect of vinculin KO by fitting cell traction and retrograde actin flow measured in MEF vinculin-KO cells21 to the WT-2 model. For this purpose, we used the dissociation rate of talin-based molecular clutches as a model-fitting parameter, because molecular clutches in MEF vinculin-KO cells are expected to be less stable due to the loss of vinculin–actin interactions that stabilize talin association with the actin cytoskeleton39,40,41. As shown in Fig. 4c,d, the WT-2 model correctly predicted a decrease in cell traction and an increase in retrograde actin flow compared to MEF WT cells in this case (blue curve). The fitted dissociation rate of molecular clutches showed a 30% increase compared to MEF WT cells, consistent with vinculin having a role in stabilizing molecular clutches. The fitting further improved when we added the myosin II density (σm) as another model-fitting parameter to phenomenologically account for the loss of tension transferred by vinculin molecules to talin (Fig. 4c,d, magenta curve). In this case, the model predicted a 60% increase in the dissociation rate of molecular clutches and a 20% decrease in the number of myosin II molecules exerting a mechanical load on molecular clutches. The decrease in myosin II density compensates for the increases in retrograde actin flow caused by the increase in the dissociation rate of molecular clutches and at the same time reduces cell traction, thus providing a better fit to the experimental data obtained in MEF vinculin-KO cells. Thus, the fitting results indicate that vinculin influences both the mechanical load of molecular clutches and their stability, which is in good agreement with published experimental data21.
Fig. 4: Vinculin recruitment modulates molecular-clutch stability and force-loading rate.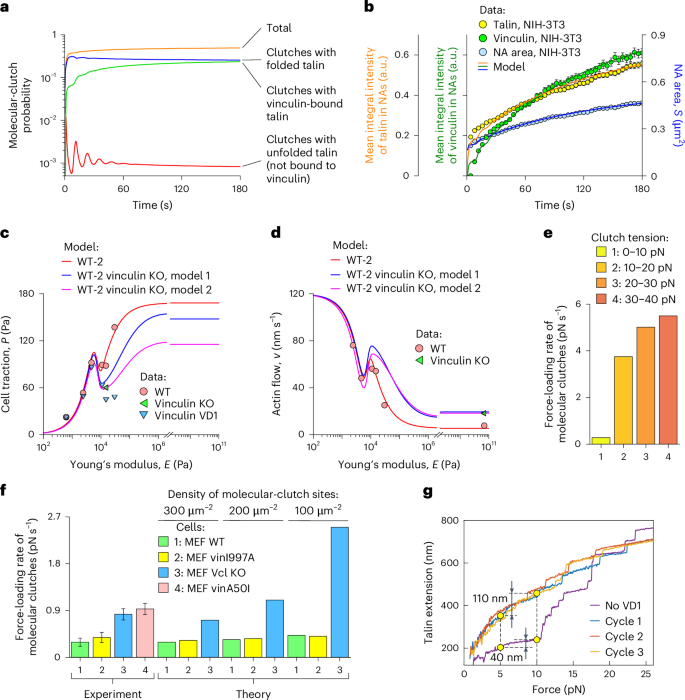
a, Numerical solution of the master equation describing NA maturation (Supplementary equation (I1)). The calculations show that the occupancy probability of sites available for molecular-clutch formation by molecular clutches with folded talin (blue curve) reaches a steady-state level within 10–20 s, whereas the amount of vinculin-bound molecular clutches (green curve) grows more slowly due to the limited pool of molecular clutches with force-unfolded talin (red curve). b, Total internal reflection fluorescence measurements of NA area (blue) and also talin (yellow) and vinculin (green) intensities in NAs in NIH-3T3 cells (mean ± s.e.m., N = 437 peripheral NAs pooled from four cells), fitted to the talin WT model. Talin accumulates first, because for vinculin to bind to it requires the unfolding of the mechanosensitive R3 domain of talin. c,d, Retrograde actin flow (d) and cell traction (c) data for WT (red circles), vinculin-KO (green triangles) and vinculin VD1-expressing MEF cells (blue triangles)13,21 fitted to the WT-2 model, which accounts for vinculin-dependent changes in the dissociation rate and tension of molecular clutches. The fit shows that vinculin enhances the stability and mechanical load of molecular clutches. e, Force-loading rates of molecular clutches predicted by the model at their different tensions in mature FAs. Higher force-loading rates were predicted for molecular clutches under higher tension. f, Force-loading rates of molecular clutches in the presence of different vinculin mutants predicted by the talin WT model. KO of vinculin (blue) or vinculin with reduced talin binding affinity (vinA50I, red) markedly accelerates the force-loading rate of molecular clutches and increases the sensitivity to the density of sites available for molecular-clutch formation, whereas vinculin with reduced actin-binding affinity (vinI997A, yellow) has little effect compared to MEF WT cells (green). Experimental data were digitalized from ref. 20 (mean ± 95% confidence interval for three independent experiments). g, Force–extension curves of talin alone (no VD1) and in the presence of vinculin VD1 (cycles 1–3)22. Binding of vinculin VD1 to force-unfolded talin domains prevents their refolding, increasing talin extension in the 5–10 pN range by almost threefold, thereby softening talin. Vcl, vinculin. Panel g adapted from ref. 22 under a Creative Commons license CC BY 4.0.
We then calculated the dynamics of the talin-based molecular-clutch system in the presence of vinculin–talin interactions. To do this, we added three kinetic rates to the talin WT model, shown in Supplementary Table 4. These rates describe the kinetics of vinculin association or dissociation from the unfolded mechanosensitive R3 domain of talin (\({k}_{{\rm{on}}}^{{\rm{R3v}}}\) and \({k}_{{\rm{off}}}^{{\rm{R3v}}}\), respectively) and the formation of molecular clutches by vinculin-bound talins (\({k}_{{\rm{on,v}}}^{0}\); Supplementary Appendix I). The values for the first two rates were taken from previously published single-molecule experimental measurements25. The value of the \({k}_{{\rm{on,v}}}^{0}\) rate was chosen based on the assumption that vinculin-bound talins remain inside FAs even after the dissociation of molecular clutches from the substrate, so that they can readily form new molecular clutches compared to vinculin-unbound talins. Furthermore, based on previously published experimental data22, it was assumed that by binding to mechanically unfolded talin, vinculin locks it in the unfolded, more elastic state until it dissociates from talin. Finally, the effect of vinculin-mediated stabilization of talin-based molecular clutches was modelled by increasing the dissociation rate of such molecular clutches when vinculin is not bound to them to a value found by fitting the cell traction and retrograde actin flow data shown in Fig. 4c,d.
As shown in Fig. 4a,b, the evolution of the molecular-clutch system predicted by the model in this case has dynamics like those in the formation of NAs, as the kinetics of talin and vinculin accumulation within NAs and changes in NA area are like those observed in experiments performed on NIH-3T3 cells. The total amount of talin in NAs was found to increase rapidly, reaching within seconds ~50% of the total change in integral talin intensity in NAs observed during the first 3 min, whereas vinculin recruitment due to the binding to talin had a slower trend. Further calculations showed that the average force-loading rate of molecular clutches at various tension values in the range 0–30 pN also agrees well with experimental observations that demonstrate a highly nonlinear change in the force-loading rate with the tension experienced by molecular clutches20 (Fig. 4e). Furthermore, the average force-loading rate of molecular clutches is in the range 0.2–5 pN s−1, which is in good agreement with the experimental results obtained using tension-gauge DNA sensors19,20.
We then tested the effects of vinculin-KO and vinculin A50I and I997A mutants with reduced binding affinity to talin and actin, respectively, on the force-loading rate of molecular clutches. To do this, vinculin-KO/A50I was treated in the model by setting \({k}_{{\rm{on}}}^{{\rm{R3v}}}=0\) (no vinculin binding to talin). Additionally, the model parameter α, which describes the average number of new sites available for molecular clutch formation that are added to NAs and FAs upon unfolding of the mechanosensitive R3 domain of talin and subsequent binding of vinculin to it, was set to zero: α = 0 (no vinculin-mediated force-induced enhancement of NAs and FAs). As for the vinculin I997A mutant, the same \({k}_{{\rm{on}}}^{{\rm{R3v}}}\) and α values were used as in the case of MEF WT cells, but \({k}_{{\rm{on,v}}}^{0}\) was set to zero: \({k}_{{\rm{on,v}}}^{0}=0\) (as there is no rebinding of vinculin-associated molecular clutches after their dissociation from the substrate, because the vinculin I997A mutant is potentially unable to retain talin in NAs and FAs due to its reduced binding affinity for actin). In addition, for both vinculin-KO/A50I and vinculin I997A, the dissociation rate of molecular clutches was set to a higher level and the myosin II density was set to a lower level in the model calculations compared to MEF WT cells, according to the results shown in Fig. 4c,d. We calculated the effects of these mutants on the molecular-clutch dynamics on a rigid substrate coated with different ligand densities. The results showed that vinculin-KO and vinculin mutants strongly affected the force-loading dynamics of molecular clutches (Fig. 4f). In good agreement with experimental observations20, an increase in the average force-loading rate was observed for the vinculin-KO/A50I mutant, whereas the vinculin I997A mutant resulted in a negligible change in the force-loading rate (Fig. 4f). Furthermore, our model also correctly predicted the dependence of the force-loading rate of molecular clutches on the substrate ligand density, as there was an increase in the force-loading rate at lower ligand densities in all experimental conditions, with the most pronounced effect observed under vinculin KO conditions (Fig. 4f).
Overall, these results indicate that the mechanical stability of molecular clutches and the nonlinear force response of talin regulated by vinculin binding strongly affect the dynamics of molecular clutches. On the one hand, vinculin depletion reduces the stability of molecular clutches, leading to a decrease in cell traction under vinculin KO conditions. On the other hand, the binding of vinculin to the mechanosensitive R3 domain of talin and the locking of the latter in the unfolded state leads to an overall softening of talin, reducing the build-up of talin tension. In addition, due to the nonlinear force response of talin, which exhibits higher elasticity at lower stretching forces, the tension build-up in talin will be slower in the lower force range compared to the higher force range, in good agreement with experimental observations (Fig. 4e,g).
To illustrate the contribution of talin elasticity to the force-loading dynamics of molecular clutches, we produced qualitative estimates based on single-molecule measurements of the force response of talin in the absence and presence of vinculin binding22. As shown in Fig. 4g, the measured end-to-end extension of the folded talin under a tension of 10 pN is ~40 nm greater than that under a tension of 5 pN. For talin with all nine domains containing unfolded vinculin binding sites, the difference in the end-to-end extension of talin at the same tension values is ~110 nm. Considering the retrograde actin flow of ~7–10 nm s−1 obtained from fitting experimental data to the talin WT model with rigid substrates (E ≥ 1 MPa; Fig. 2d), we easily found the values of the force-loading rate in both cases to be ~0.9–1.3 and ~0.3–0.5 pN s−1 in the absence and presence of vinculin binding to talin, respectively, which are in good agreement with experimental measurements20 (Fig. 4f, experiment). This effect of vinculin on talin stiffness and force-loading rates of molecular clutches is mediated solely by vinculin binding to talin and does not require vinculin to bind to actin. Accordingly, our model predicts that the force-loading rates of molecular clutches in MEF WT cells and MEF vinculin I997A cells should be very similar, which is also in good agreement with experimental data (Fig. 4f).
Finally, using the same parameter values fitted for MEF WT cells, our model was also able to reproduce experimental observations of the mechanosensitive cell-adhesion behaviour on liquid-like viscoelastic substrates, which in the simplest case can be described by the Maxwell model, thus highlighting the robustness of our model predictions (Extended Data Fig. 4).
Steady-state behaviour and bifurcation of the clutch system
To further investigate the dynamic behaviour and stability of cell-adhesion complexes under different physiological conditions, we used the linear KD and linear WT models, which were found to accurately fit cell traction and retrograde actin flow measurements made in cells plated on substrates of different elasticities.
First, we mapped the bistability region in the space of model parameters. To do this, we varied the values of the spring constant of the intracellular part of molecular clutches (kc) and the myosin II density (σm) in the linear KD and linear WT models (Fig. 5). As a result, for the MEF Talin 1 KO, Talin 2 shRNA cells, the bistability region was found to be localized at moderate values of the myosin II density, close to the parameter range of the linear KD model corresponding to MEF Talin 1 KO, Talin 2 shRNA cells (Fig. 5a,e). This finding indicates that molecular clutches probably experience the bistability in myosin II-depleted regions of such cells that can often be found at the cell periphery42. Indeed, experiments have recently shown that filopodia exhibit both strong and weak adhesion to fibronectin-coated substrates in a myosin II-dependent manner42.
Fig. 5: Bistability of cell adhesion.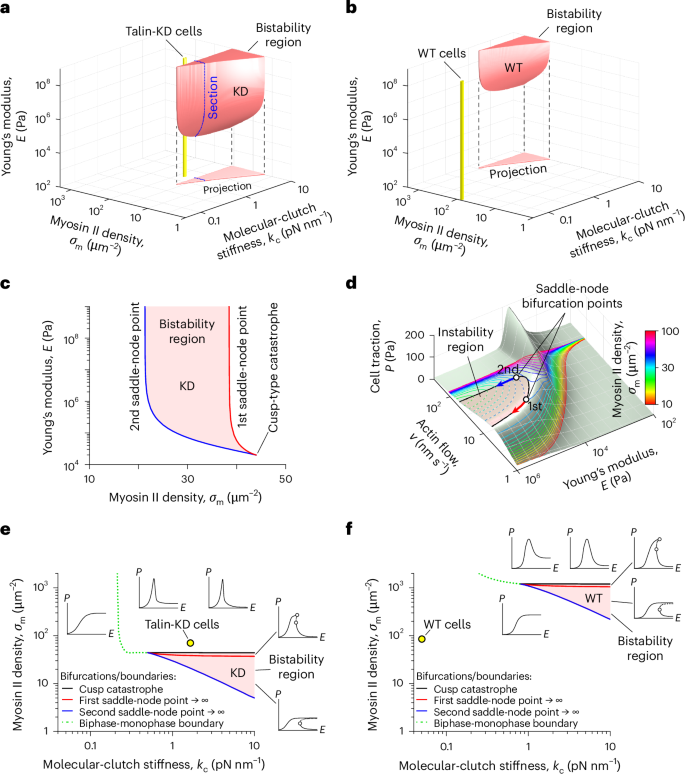
a,b, Stability diagrams of the linear KD (a) and linear WT (b) models. Three-dimensional red shapes and triangles denote the bistability regions and their projections, respectively. Yellow cylinders represent the model parameter ranges corresponding to MEF Talin 1 KO, Talin 2 shRNA and MEF WT cells. The blue dotted contour in a indicates a cross section of the bistability region detailed in c. Notably, talin-deficient MEF cells lie close to this region, whereas MEF WT cells are far from it, indicating that the high elasticity of talin stabilizes NAs and FAs. c, Close-up of a cross section of the bistability region indicated in a. Its boundaries are formed by the trajectories of the two saddle-node points shown in d. The bistability region arises from a cusp-type catastrophe when the rigidity of the intracellular part of molecular clutches is sufficiently large. d, Cusp catastrophe experienced by the molecular-clutch system. The pale green surface depicts cell traction (P) as a function of the retrograde actin flow (v) and substrate elasticity (E) in the linear KD model. The solid and dashed curves denote the stable and unstable branches of the solution for different myosin II densities (σm). Reducing σm to ~44 μm−2 results in the appearance of two saddle-node bifurcation points, a typical sign of a cusp catastrophe. Further decreasing σm shifts these points along the surface, outlining an instability region that includes only the unstable branches of cell traction curves. e,f, Stability diagrams of cell adhesion complexes in the case of MEF Talin 1 KO, Talin 2 shRNA cells (e) and MEF WT cells (f) obtained by projecting the bistability regions shown in a and b onto the horizontal plane. The black, red and blue solid curves mark the onset of the cusp catastrophe and bifurcations due to saddle-node points moving to infinity, which lead to the formation of biphase–monophase boundaries (green dotted curves), which affect the shapes of cell traction curves both within and beyond the bistability region. The insets around the bistability region illustrate representative cell traction curves within each domain. The graphs show that the elasticity of the intracellular part of molecular clutches and the myosin II density have a profound effect on the mechanosensitive behaviour of cell adhesion.
In addition, we fitted previously published experimental data collected for MEF Talin 1 KO, Talin 2 shRNA cells treated with a myosin II inhibitor, blebbistatin13, to the linear KD model. We found that these cells begin to develop bistable cell-adhesion behaviour when the density of myosin II motors in them decreases by ≳1.6 times (15 μM blebbistatin case; Extended Data Fig. 5a), with a further decrease in the myosin II density leading to a more pronounced bistability of cell adhesion (50 μM blebbistatin case; Extended Data Fig. 5a). On the other hand, blebbistatin-treated MEF WT cells did not seem to exhibit bistable cell-adhesion behaviour (Extended Data Fig. 5b), mainly due to the very high elasticity of talin-based molecular clutches, which results in MEF WT cells being far from the corresponding bistability region in the model parameter space (Fig. 5b,f). This finding indicates that talin molecules could potentially play an important role in stabilizing NAs and FAs during their maturation.
The existence of stable stationary states at each value of Young’s modulus for the substrate indicates that the molecular-clutch system should converge over time to one of these states, which, thus, represent possible steady states of the system. To find out how quickly the molecular-clutch system reaches these stationary states starting from an initial configuration with zero adhesion bonds between a cell and the substrate, we used the finite-difference method to numerically solve the master equation describing the time evolution of the molecular-clutch system (Supplementary equation (B10)). Both the linear WT and linear KD models predicted the rapid convergence of key experimental observables, such as cell traction and retrograde actin flow, to their stationary values within ~10–20 s (Extended Data Figs. 6a,b and 7a,b). The probability distribution of molecular-clutch extension also demonstrated rapid convergence to the steady-state distribution given by equation (9) in as little as 20 s (Extended Data Figs. 6c and 7c). These results are in good agreement with previous experimental observations showing that the retrograde flow of actin filaments in filopodia or near the edges of living cells occurs at an almost constant rate (v(t) ≈ const.)7,13,21,42,43, indicating that cell-adhesion complexes should function close to a steady state.
Furthermore, the characteristic relaxation time of the molecular-clutch system to the steady state predicted by our model for elastic-like substrates was two to four orders of magnitude less than the average lifetime of FAs (Extended Data Figs. 6e and 7e and Supplementary Table 5), indicating that they spend more than 98% of their time in a steady or quasi-steady state. In addition, from Supplementary Table 5, it is clear that the experimentally measured characteristic binding and dissociation times of vinculin and paxillin to or from FAs are an order of magnitude greater than the characteristic relaxation time of the molecular-clutch system to a steady state. This result indicates that talin may serve as a rapid response protein that helps establish the initial landscape of molecular clutches in a substrate-mechanosensitive manner, which can subsequently be reinforced and shaped by vinculin or paxillin into matured FAs, in good agreement with previous experimental data13,21,26,27,44.