Algorithm discovery has entered its own belle époque. With the latest performance gains of IBM quantum hardware and software, researchers are better positioned than ever before to develop and improve algorithms that will bring us closer to quantum advantage.
Recently, researchers led by Dr. Daniel Lidar’s team at the University of Southern California (USC) published results in Physical Review X that demonstrate exponential algorithmic speedup for a modified version of Simon’s problem using IBM quantum computers. This paper offers one of the first proofs of quantum scaling speedup not dependent on unproven assumptions regarding the limitations of classical methods.
Put simply, the team ran circuits on noisy quantum hardware up to 126 qubits, demonstrating that as the problem increased in size, the speedup scaled exponentially for quantum. However, past 58 qubits, noise inherent to today’s quantum computers allowed classical to win.
A key part of algorithmic development is identifying the problems for which quantum will provide a speedup over classical methods, as well as determining what kind of speedup is expected. This is an effort that requires novel strategies on today’s noisy devices.
“The holy grail of quantum computing has always been to demonstrate that we can execute quantum algorithms with an exponential scaling speedup,” says Lidar. An exponential scaling speedup means that as the problem size increases owing to the addition of variables, the gap between quantum and classical performance keeps growing, to the advantage of the quantum side.
Until this point, only more modest types of speedup, such as polynomial, have been demonstrated on quantum hardware—including that shown by Lidar and Bibek Pokharel for the Bernstein-Vazirani algorithm in a 2023 Physical Review Letters article.
A quantum guessing game
Simon’s problem is an oracle-based game: players attempt to correctly guess a hidden bitstring (bb), known only to the oracle (a black box), in as few queries as possible. Lidar’s team modified the game slightly by restricting the Hamming weight—effectively, the amount of 1s in the bitstring—to limit the complexity of the circuit. The rules for this version of Simon’s problem go like this:
A secret bitstring b∈0,1b∈{0,1}nn is chosen behind the scenes. This bitstring has a fixed Hamming weight ww, meaning it contains exactly ww 1s in the bitstring.
A mystery function ff is defined, such that f(x)=f(y)f(x) = f(y), if and only if x=yx = y or x=y+bx = y + b. In other words, each output is shared by exactly two inputs, offset by the hidden bitstring bb. Correctly guessing the two bitstrings that are offset by the hidden bitstring reveals the function of the same value.
You are not privy to the function—you can access only the oracle, which you can query using any input x∈0,1x∈{0,1}nn to get f(x)f(x). To query the oracle, you can use either a classical or quantum computer. However, with a quantum computer, your query can be in superposition; that is, it can be a complex linear combination of two states until measured.
For classical computers, finding this hidden bitstring proves to be exponentially hard relative to the number of bits in the hidden bitstring. In 1994, Daniel Simon developed an algorithm providing theoretical proof that this problem—when run on ideal, noiseless quantum computers—could be solved in very few queries to the quantum oracle, providing exponential advantage over the best probabilistic classical algorithms.
While there is no known practical application for Simon’s problem, it is a stepping-stone to Shor’s period-finding problem, which does not rely on an oracle. Both are examples of the abelian hidden subgroup problem, where the commutative property of elements in the group—the property that tells us the order of operations does not matter—is leveraged to discern the hidden structure in the group.
Extracting performance from near-term quantum computers
Lidar and team sought to take the promise of exponential speedup for Simon’s algorithm from paper to machine by demonstrating it on today’s pre-fault-tolerant quantum hardware, ultimately running their experiment on two 127-qubit IBM Quantum Eagle processors, ibm_brisbane and ibm_sherbrooke.
To measure the scaling, the researchers defined a metric called NTS, or Number of Oracle Queries to Solution. A classical player needs roughly Ω(nΩ(nw/2{w/2})) queries on average, meaning that for a problem size n, the classical device requires Ω(nΩ(nw/2{w/2})) queries at the lower bound (ΩΩ), or the best-case performance. On the other hand, an ideal (noiseless) quantum player needs at best only O(wlogn)O(w logn) queries to solve the problem. A quantum player consistently solving the problem with fewer queries indicates a quantum speedup in the oracle model.
To achieve the speedup experimentally on near-term devices, the researchers developed methods that employed a few key techniques:
Circuit optimization
To prevent noise from accumulating too much, the team needed to limit the circuit depth. Accordingly, they reduced the number of required quantum logic operations to transpile the naïve Simon’s circuit into a shallower circuit. “We relied heavily on the existing functionality of Qiskit,” Lidar notes. “Everything we did to improve the results was built on top of it.”
Dynamical decoupling
The researchers also introduced dynamical decoupling to suppress the noise in the circuit—perhaps the most critical element of their modified workflow. Oftentimes, the circuits necessary for a given algorithm require that some qubits sit idle while they wait for other qubits to have operations performed on them. During this time, the idle qubits can experience dephasing noise, which can result in decoherence.
Dynamical decoupling involves adding microwave pulse sequences to reverse the effects of the noise arising from both unwanted qubit interactions with the environment and unwanted interactions between the qubits themselves, otherwise known as crosstalk. As illustrated in the figure below, dynamical decoupling significantly improves the quantum results, yielding a scaling curve much closer to the ideal (noiseless) quantum result.
Measurement error mitigation
Lastly, they applied measurement error mitigation to find and correct errors introduced during the measurement process, following dynamical decoupling.
Through these optimization and noise suppression efforts, the researchers were able to show that a quantum player could win exponentially faster than any classical one. They observed the speedup on problem sizes up to 58 qubits for Hamming weights up to w=7w = 7. For Hamming weights of w=8w = 8 and w=9w = 9, the quantum algorithm no longer showed advantage due to the increased circuit depth.
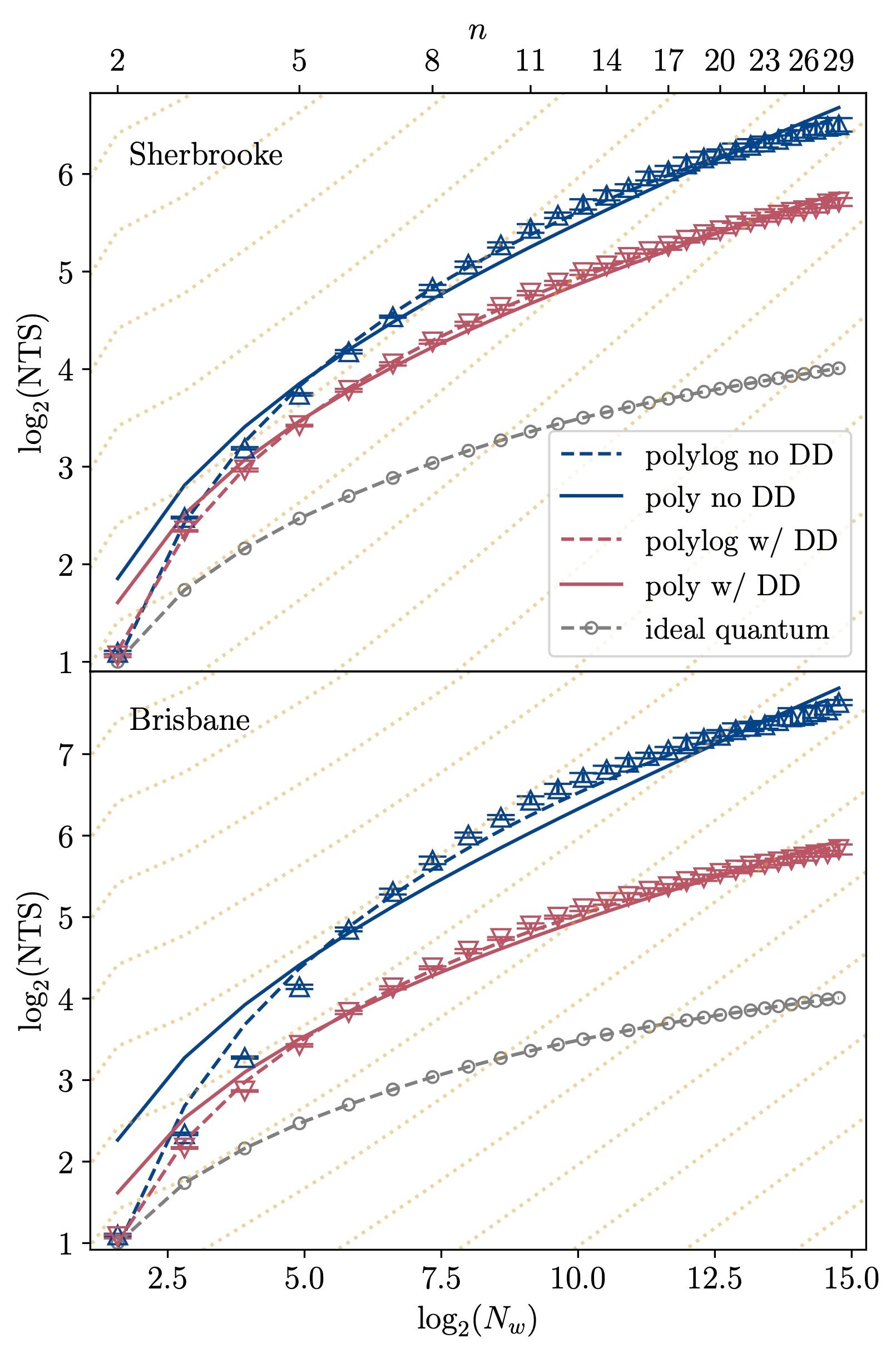
The figure above shows the algorithmic quantum speedup for Simon’s problem observed on `ibm_sherbrooke` and `ibm_brisbane`. The X axis represents the problem size on a log scale, or number of possible bitstrings of Hamming weight up to w, where w is the hidden bitstring. The Y axis represents the number of queries to the oracle to obtain the correct answer. The yellow dotted lines signify the classical scaling, which is exponential in nature. The grey line represents the ideal (noiseless) quantum curve, while the blue line shows the quantum result without dynamical decoupling and the red line shows the quantum result with dynamical decoupling applied. As evidenced by the curves, dynamical decoupling yields a shallower slope for the quantum processor and more closely reflects the ideal result. The solid lines are fits to polynomial scaling, while the dashed lines are fits to logarithmic scaling; the latter is better, evidencing the exponential improvement over the classical scaling.
Extending utility to advantage with error mitigation
As quantum hardware continues to mature, the team expects to be able to extend the type of speedup demonstrated here to quantum algorithms that are not oracular. In particular, they are interested in problems that do not rely on assumptions about classical limitations to provide verification of quantum advantage.
“We’re showing that already, today’s quantum computers firmly lie on the side of quantum advantage, without any conjectures,” Lidar explains. “The significance here is that it gives other, more practical utility-scale results a more solid footing to stand on.”
This work serves as an important example of the role algorithm discovery plays in extracting value from near-term quantum hardware—giving renewed impetus to the quantum community to experiment with algorithms to bring quantum advantage closer.

