Crystal structure
The crystal structure of the approximant decagonal QC Al13Os4 adopts a low-symmetry monoclinic structure with space group C2/m (No. 12) and C2h point-group symmetry (see Fig. 1a, b), isostructural to the Y phase of Al13−x(Co4(1−y)Ni4y) or Al11Co427,28. Figure 1c shows the powder X-ray diffraction pattern (XRD) and Rietveld refinement (detailed structural parameters and Wyckoff positions given in the Supplementary Information Supplementary Note 1, Table S1 and Fig. S1).
Fig. 1: Crystal structure characterization of the decagonal quasicrystal approximant Al13Os4.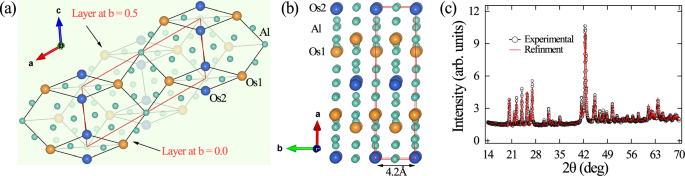
a Crystal structure of the decagonal approximant characterized with distorted pentagons and rhombi. The aperiodic layer at \(\overrightarrow{b}=0.0\) connects to the layer at \(\overrightarrow{b}=1/2\) to form an approximant decagonal structure. The red rhombus outlines the unit cell. b Periodic repetition of the unit cell along the \(\overrightarrow{b}\) direction, with a periodicity of 4.2 Å. c Powder X-ray diffraction pattern (black markers) and Rietveld refinement (red line) of Al13Os4.
The structure comprises of two quasi-periodic layers stacking along the \(\overrightarrow{b}\) direction with a periodicity of ~ 4 Å. A quasiperiodic atomic layer in the \(\overrightarrow{b}=0\) plane connects to another layer at \(\overrightarrow{b}=1/2\) plane through a shift in the lattice constant by a/2 to form a periodic unit cell (Fig. 1b). It consists of slightly distorted pentagons and rhombi (Fig. 1a), with an Al atom occupying one vertex of the pentagon and Os atoms occupying the remaining vertices. Three Al atoms also lie in this Os-Al pentagon. Smaller Al pentagons, made up of five Al atoms with an Os atom at the center, also appear in the adjacent layers. Despite slight differences in Al and Os occupancy, the local structural configuration in the two quasi-periodic layers is nearly identical. In the periodic approximant phase, pentagonal elements are distorted, unlike the regular pentagons in the decagonal quasicrystal phase, representing the primary difference between the two phases27,29. The repetitive arrangement of distorted pentagons and rhombi that tile in the plane to generate the periodic crystal structure shown in Supplementary Fig. S2 (Supplementary Note 2). It is important to note that a decagonal QC with two quasiperiodic layers with a periodicity length of about 0.4 nm is the most anisotropic case, whereas other decagonal QCs have four, six, and eight layers in a periodic unit with periodicities of about 0.8, 1.2, and 1.6 nm, respectively, exhibiting progressively lower anisotropies.
Bulk superconductivity
Figure 2a presents the temperature-dependent electrical resistivity ρ(T) of Al13Os4 under zero-applied magnetic field. A sharp decrease in ρ(T) to zero at a transition temperature Tc = 5.47(2) K confirms the onset of superconductivity, the highest Tc observed to date in any known quasicrystals and approximants (see Supplementary Table S2 for details). The high-temperature behavior of ρ(T) is metallic, which is well described by Wiesmann’s parallel resistor model (black solid line in Fig. 2a). The residual resistivity ratio, ρ(300)/ρ(10) = 7.5, further corroborates the metallic nature of the system (additional details on fitting parameters, Kadowski-Woods ratio, and the Hall measurement data are given in Supplementary note 2).
Fig. 2: Bulk superconductivity characterization of the decagonal quasicrystal approximant Al13Os4.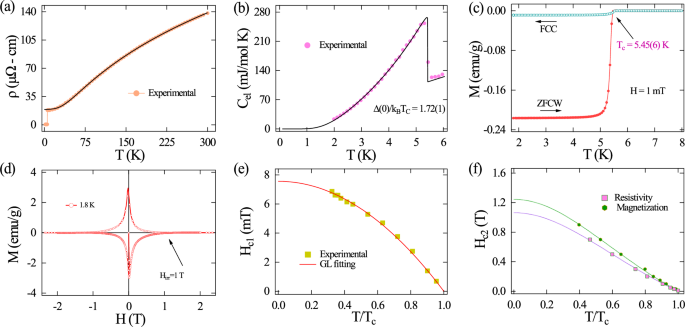
a Temperature dependence of resistivity ρ(T) at H = 0 T, showing the superconducting transition at Tc = 5.47(2) K. b Temperature-dependent electronic specific heat (Cel), with the fitting of data using weak-coupling BCS model (solid black line). c Temperature-dependent ZFCW and FCC magnetization at an external field of 1.0 mT, demonstrating clear superconducting transition. d Magnetization with variation of the magnetic field at 1.8 K. e, f Temperature-dependent lower Hc1 and upper Hc2 critical fields, revealing the large upper critical field.
Specific heat measurements reveal a lambda-shaped anomaly observed at Tc = 5.44(2)K, confirming bulk superconductivity consistent with resistivity and magnetization data (see Supplementary Fig. S3). Figure 2b, shows temperature-dependent electronic specific heat, fitted with the BCS model. The fitting results yield a superconducting gap value (\(\frac{\Delta (0)}{{k}_{B}{T}_{c}}\)) of 1.72(1), indicating weak coupling BCS superconductivity in Al13Os4. Additionally, the density of states at the Fermi level D(EF) estimated to be 9.15(4) states eV−1 f.u.−1, and the Debye temperature θD, 340(4) K, comparable to those found in elemental Os and Al, the approximant phase of quasicrystals, and other complex intermetallic compounds14. Using the McMillan model, the electron-phonon coupling strength λe−ph is estimated to be 0.63(1), indicating weakly coupled superconductivity in Al13Os4. A detailed mathematical description of this analysis is provided in Supplementary note 2.
Figure 2c displays the temperature-dependent magnetization of Al13Os4 measured in a 1 mT applied field. Both the zero field-cooled warming (ZFCW) and the field-cooled cooling (FCC) curves exhibit a sharp diamagnetic response below Tc = 5.45(6) K, confirming the Meissner effect and the onset of superconductivity. The observed difference between the ZFCW and FCC curves is attributed to flux pinning, a characteristic of type-II superconductors (Fig. 2d). The full Meissner fraction observed in the ZFCW measurement indicates complete flux exclusion upon initial cooling. In contrast, the negligible flux expulsion during the FCC mode suggests the presence of strong flux pinning in Al13Os4 compound. The AC susceptibility and magnetization loop further confirm the superconducting transition and vortex pinning (see Supplementary Fig. S4). Using M versus H and M versus T data and applying the Ginzburg-Landau (GL) relations (Fig. 2e, f) the lower and upper critical fields are determined to be obtained as Hc1 = 7.5(4) mT and Hc2 = 1.24 (1) T, respectively (details in Supplementary Note 2, Fig. S5). From these values, two important length scales are extracted, the penetration depth λGL(0) = 249(5) nm and coherence length ξGL(0) = 16.2(9) nm. The GL parameter κGL = λGL(0)/ξGL(0) = 15.3(1) indicates strong type-II superconductivity. The thermodynamic critical field is obtained as Hc = 58.3(8) mT. Moreover, the calculated Maki parameter αM = 0.14 suggests that the Pauli limiting effect has a negligible influence on superconductivity, with orbital limiting being the dominant factor.
μSR results
To further investigate the superconducting gap symmetry and ground-state properties of Al13Os4, we performed Muon spin rotation and relaxation (μSR) measurements at ISIS, RAL UK, employing both transverse field (TF) and longitudinal field (LF) geometries, as illustrated in Supplementary Fig. S6 (Supplementary Note 2).
TF-μSR and fully gapped superconductivity
TF-μSR experiments are used to examine the superconducting gap symmetry by measuring the magnetic penetration depth and field distribution in the mixed state. To establish a well-ordered flux line lattice (FLL), experiments were performed under field-cooled conditions. Figure 3a shows the asymmetry spectra (precession signal) measured above and below Tc in an applied field of 30 mT, where the faster relaxation rate at 0.5 K compared 7 K reflects the inhomogeneous field distribution from the FLL. In all temperature ranges, time domain TF-μSR asymmetry spectra are well described by the Gaussian-damped oscillatory function given as,
$$A(t) = {A}_{1}exp \left(-\frac{1}{2}{\sigma }^{2}{t}^{2}\right)\cos ({\gamma }_{\mu }{B}_{1}t+\phi )\\ +{A}_{2}\cos ({\gamma }_{\mu }{B}_{2}t+\phi ),$$
(1)
where A1 and A2 denote the initial asymmetries corresponding to the sample and non-relaxing background from the silver sample holder, B1 and B2 are the local magnetic fields sensed by the muons in the sample and sample holder, and γμ/2π = 135.5 MHz/T is the muon gyromagnetic ratio. ϕ denotes the common phase offset. The Gaussian depolarization rate, σ, is given by \({\sigma }^{2}={\sigma }_{N}^{2}+{\sigma }_{sc}^{2}\), where σN = 0.219 μs−1 is the temperature-independent depolarization rate associated with the nuclear dipole moment and σsc represents the depolarization rate from the FLL. The temperature dependence σsc exhibits a plateau at low temperatures. Subsequently, it decreases as the temperature increases before finally reaching zero at Tc (Fig. 3b). To determine the superconducting gap, the temperature-dependent penetration depth λ−2(T) ∝ σsc was fitted with an isotropic s-wave BCS superconductor in the clean limit30,
$$\frac{{\sigma }_{sc}(T)}{{\sigma }_{sc}(0)}=\frac{{\lambda }^{-2}(T)}{{\lambda }^{-2}(0)}=1+2 \int _{\Delta (T)}^\infty \left(\frac{\partial f}{\partial E}\right)\frac{EdE}{\sqrt{{E}^{2}-\Delta {(T)}^{2}}},$$
(2)
where λ(0) is the London penetration depth, \(f={[1+{e}^{(E/{k}_{B}T)}]}^{-1}\) is the Fermi distribution function, and Δ(T) is the BCS superconducting gap function given as Δ(T) = Δ0tanh[1.82\({(1.018(({T}_{c}/T)-1))}^{0.51}\)]. Fitting of λ−2(T) with Eq. (2) provides a superconducting gap as Δ(0) = 0.79(3) meV. The normalized gap, Δ(0)/kBTc = 1.78(6), is consistent to that expected for a BCS weak coupling superconductor. To determine the penetration depth λμSR(0), the following relation used where kGL ≥ 5 and H ≤ Hc231;
$${\sigma }_{sc}(\mu {s}^{-1})=4.854\times 1{0}^{4}(1-h)\left[1+1.21{(1-\sqrt{h})}^{3}\right]{\lambda }^{-2},$$
(3)
with h = H/Hc2(0) the reduced field. The calculated value of λμSR(0) = 268.6(7) nm closely matches the values from the magnetization as well as those obtained through the analysis of the London penetration depth. Considering the measured residual resistance, we derive a ratio of BCS coherence length and the electronic transport mean free path (ξ0/le) that approaches the clean limit of the superconductor [See Supplementary note 2 for individual electronic parameter calculations]31.
Fig. 3: Microscopic characterization of superconductivity in the decagonal quasicrystal approximant Al13Os4.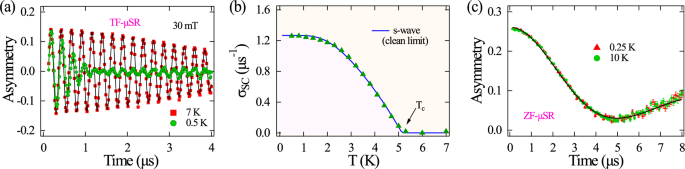
a TF-μSR spectra obtained at 30 mT, both above and below superconducting Tc with relevant fits. b Zero field (ZF)-μSR spectra above and below Tc with a solid line fit representing the product of the static Kubo-Toyabe function and an exponential decay function. c Temperature-dependent superconducting relaxation rate (σSC) fitted with the isotropic conventional s-wave model.
ZF-μSR and preserved time-reversal symmetry
We further employ zero-field (ZF)-μSR measurements to probe spontaneous magnetization linked to time-reversal symmetry breaking in the superconducting state. The overlapped ZF-μSR asymmetry spectra below and above Tc (Fig. 3c) show no detectable spontaneous magnetization, confirming the preserved time-reversal symmetry in Al13Os4. The best description of the ZF spectra is given as,
$$A(t)={A}_{0}{G}_{KT}(t) \,exp \,(-\Lambda t)+{A}_{bg},$$
(4)
where A0 is the initial sample asymmetry and Abg is the non-decaying background from muons stopped in the silver sample holder. The Gaussian static Kubo-Toyabe (KT) function (GKT(t)) is given as32:
$${G}_{KT}(t)=\frac{1}{3}+\frac{2}{3}(1-{\Delta }^{2}{t}^{2}) \,exp \left(-\frac{{\Delta }^{2}{t}^{2}}{2}\right),$$
(5)
The relaxation parameter Δ is associated with randomly oriented, static local fields from nuclear moments, and the electronic relaxation rate, Λ, both remains nearly constant above and below the superconducting Tc, indicating preserved time-reversal symmetry in Al13Os4.
Electronic structure and topology
To examine the electronic topology of decagonal approximant Al13Os4, we performed first-principles calculations considering experimental parameters with C2/m symmetry. The calculated band structure and density of states (DOS) exhibit metallic behavior, with several bands crossing the Fermi level EF (Fig. 4a, b). The four bands, labeled γi=1−4, occupy the substantial area of the BZ at the Fermi level. Among these, the γ2 and γ3 bands display a 2D character with open Fermi sheets at EF (Fig. 4c). In contrast, the γ1 band exhibits 3D saddle-points energy dispersion with a large area flat band close to EF as shown in Fig. 4b. At the Γ point, the electron (blue) and hole (red) bands cross to form a saddle point with a slowly decaying quadratic dispersion along the Γ − X direction. This saddle point gives van Hove singularities (vHSs) near the Fermi level. Such features in the electronic structure are expected to enhance superconducting instability, in agreement with the experimental observations. The observed gaps and spikes in the DOS, consistent with features arising from quasiperiodicity, may thus play a crucial role in tuning superconducting properties. The proximity of the Fermi level to peaks in the density of states (e.g., vHSs) can enhance electronic correlations and potentially raise the Tc, as seen in other unconventional superconductors33.
Fig. 4: Nontrivial electronic topology of the decagonal quasicrystal approximant Al13Os4.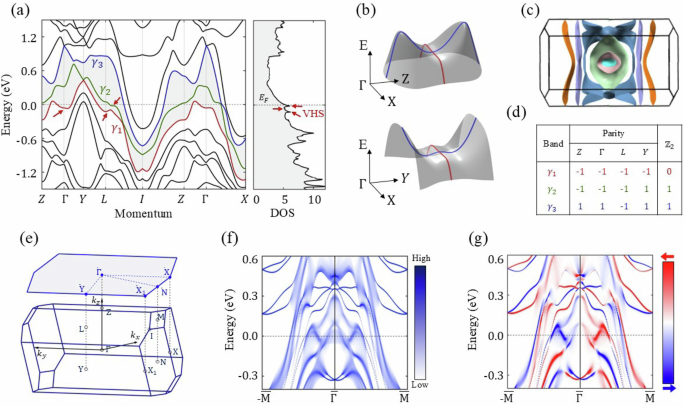
a The band structure and density of states (DOS) incorporating spin-orbit coupling. The saddle-points van Hove singularities (vHSs) are indicated by red arrows. γ1, γ2, γ3, and γ4 bands crossings the Fermi level are marked. The shaded gray color highlights a continuous band gap between various bands in the Brillouin zone (BZ). b Closeup of band structure around Γ resolving 3D saddle points with substantial flat band dispersion. c Fermi surface with various Fermi sheets in the BZ. d Parity and \({{\mathbb{Z}}}_{2}\) invariant of γ1, γ2, and γ3 bands. e Bulk BZ and (001) surface projected BZ with various high-symmetry points. f (001) surface band structure and g associated spin-texture along -\(\overline{N}-\overline{\Gamma }-\overline{N}\) direction. The spin-momentum-locked nontrivial surface states are observed within the projected bulk bandgap. Red and blue in g indicate up and down spin polarizations.
Next, we calculate the Sommerfeld-specific heat coefficient and compare it with the experimental data. From the results, we obtain a total DOS at the Fermi level, D(EF) = 5.38 states eV−1 f.u.−1. This yields a theoretical Sommerfeld specific-heat coefficient \({\gamma }_{0}=\frac{{\pi }^{2}{k}_{B}^{2}}{3}D({E}_{F})\) of 12.70 mJ mol−1 K−2, which is ~60% of the experimentally measured value of γn = 21.54(7) mJ mol−1 K−2. This difference infers that electron-mass renormalization due to saddle point could be larger than expected, potentially indicating strong correlation effects. Using the calculated (γ0) and experimental (γn) specific-heat coefficients, we estimate the electron-phonon coupling constant (λe−ph) using the relation \(\frac{{\gamma }_{n}}{{\gamma }_{0}}=(1+{\lambda }_{e-ph})\). The calculated λe−ph is 0.69, which is in close agreement with the experimental value of 0.63(1).
Having discussed the electronic properties, we now explore the topological electronic state of Al13Os4 with spin-orbit coupling (SOC) (see Fig. 4d–g). The band structure without SOC shows several nodal crossings between different bands near the Fermi level (see Supplementary Note 3, Fig. S7). These crossings form nodal lines in the bulk BZ. However, due to the lower C2h point-group symmetry and inversion symmetry in Al13Os4, the inclusion of SOC gaps out these nodal band crossings, resulting in a continuous bandgap at each k-point in the BZ. This local bandgap facilitates the calculations of the \({{{{\mathcal{Z}}}}}_{2}\) topological invariant similar to insulators34. In Fig. 4d, we show the product of parity eigenvalues at various time-reversal invariant points for bands γi=1−334. This parity analysis reveals a nontrivial \({{{{\mathcal{Z}}}}}_{2}\) invariant when either γ2 or γ3 bands are considered as valence bands. Figure 4f, g display the (001) surface band structure and corresponding spin texture. Several spin-momentum-locked surface states are seen to cross the Fermi level. Specifically, within the bulk band-inverted region around +0.3 eV, a clear nontrivial Dirac cone surface state appears inside the projected bulk bands. The lower state of this Dirac cone exhibits substantial bandwidth and crosses the Fermi level. The calculated nonzero \({{{{\mathcal{Z}}}}}_{2}\) invariant and non-trivial Dirac cone surface states confirm that Al13Os4 is \({{{{\mathcal{Z}}}}}_{2}\) nontrivial. The presence of nontrivial spin-polarized surface states can become superconducting via the bulk proximity effect, leading to unconventional superconductivity in Al13Os4.
