Estimating the global properties of quantum systems, such as their similarity to complex states, presents a significant hurdle in quantum research, and is crucial for verifying the performance of quantum computers. Qingyue Zhang, Dayue Qin, and Zhou You from Fudan University, along with colleagues, now demonstrate a new method for tackling this challenge, offering a pathway to more reliable measurements. Their approach, termed robust phase shadows, utilises a simplified set of quantum gates , specifically controlled-Z gates , making it well-suited to current quantum computing technologies like trapped ions and neutral atoms. The team rigorously proves that this method performs as well as more complex techniques, and importantly, incorporates a noise-robust extension that allows for accurate estimations even with realistic imperfections in quantum hardware, resolving a key limitation of existing methods and paving the way for scalable quantum verification.
Robust Phase Estimation with Controlled-Z Gates
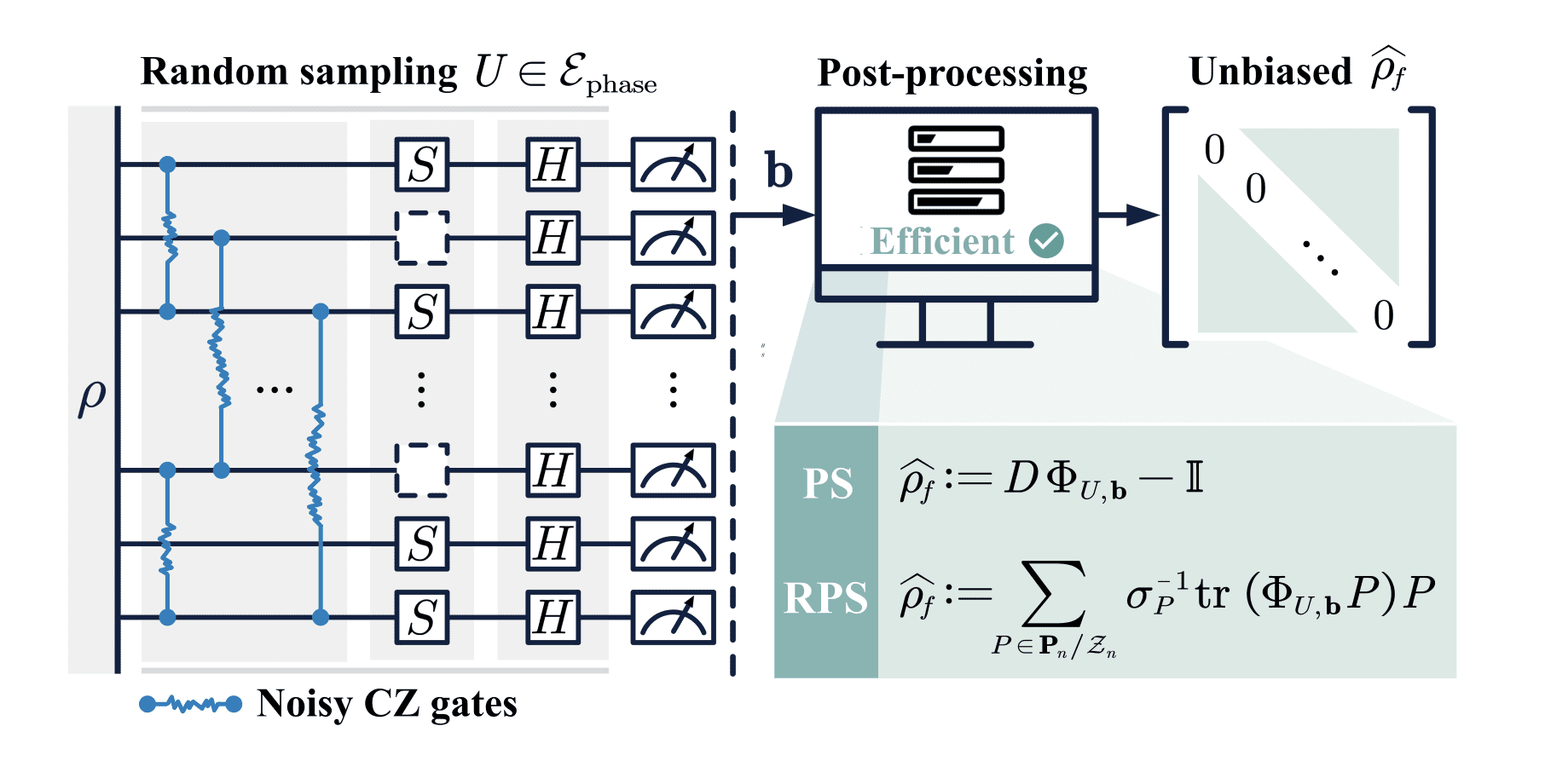
Estimating the quantum state of a system presents a significant challenge for both theoretical and experimental physicists. This research introduces the robust phase shadow scheme, a measurement framework employing random circuits that utilise controlled-Z gates as the sole entangling operation, particularly well-suited for architectures such as trapped ions and neutral atoms. Through rigorous analysis, the researchers demonstrate that phase shadows achieve performance comparable to methods based on full Clifford circuits, incorporating a noise-robust extension via classical post-processing for reliable state estimation even with imperfections in quantum hardware.
Robust State Tomography via Classical Shadows
This research details a method for robust quantum state tomography, the process of determining the quantum state of a system, using classical shadows and a technique called robust phase shadow (RPS). The core idea is to accurately determine a quantum state with a limited number of measurements, a significant improvement over traditional methods. Classical shadows achieve this by applying random quantum circuits to the unknown state and measuring the output; the resulting data contains sufficient information to reconstruct the original state. RPS is a specific implementation designed to be resilient to noise, a critical factor in real quantum devices, focusing on preserving phase information and averaging out certain errors.
The research breaks down into several key areas, establishing the background of quantum state tomography and the motivation for using classical shadows. Mathematical preliminaries, including definitions of quantum states and probability distributions, are then presented, explaining how classical shadows work and how the quantum state can be reconstructed from the measurement data. A crucial component is the description of twirling, a mathematical procedure that averages out specific types of noise by applying random transformations.
The researchers detail the specific implementation of the RPS technique, including the selection of random circuits and the measurement strategy. They define the noise model used in their analysis, specifically a Pauli error model, and explain how to calculate the statistical moments of the measurement outcomes. The core theoretical results, demonstrating the robustness of RPS to noise, are then presented, validated by numerical simulations. Further analysis explores how RPS can be extended to handle more complex noise models, including biased noise, and applied to systems of fermionic particles using different types of quantum circuits.
Key to the analysis are concepts such as Pauli errors, which represent the types of errors that occur in qubits, and twirling, which helps to mitigate these errors. The researchers use statistical moments to characterise the distribution of measurement outcomes and leverage the Haar distribution, a uniform probability distribution over transformations. They also explore matchgate circuits, specific circuits used in fermionic systems, and their property of approximating the Haar distribution, allowing the extension of the technique to fermionic quantum computing.
The implications of this research are significant. RPS offers a more robust and efficient way to determine the quantum state of a system, even in the presence of noise, which is crucial for building practical quantum computers. This technique can also be used to verify the performance of quantum devices and validate their results. Furthermore, the extension to fermionic systems opens up possibilities for developing quantum computers based on fermionic particles.
In simpler terms, imagine trying to determine the shape of a hidden object by taking measurements. Traditional methods require many measurements to obtain a clear picture. Classical shadows are like using a special type of measurement that leaves a shadow, allowing reconstruction of the shape with fewer measurements. RPS is like using a measurement that is less affected by disturbances, resulting in a more accurate reconstruction