The Institute for Public Policy Research (IPPR) has proposed large increases in gambling taxes to raise £3bn. The £3bn would be used to remove the two-child benefit limit and the household benefit, “lifting around half a million children out of poverty overnight”.

However there’s a gap between how the proposal is being pitched – taxing gambling companies on their large profits – and the reality. According to the IPPR itself it would be gamblers, not gambling companies, paying the price.

There’s also a gap in the IPPR’s calculations. This is a very large proposed tax increase – with the largest tax, remote gaming duty, rising 138%. But the IPPR’s calculation is “static” – it simply multiplies current gambling profits by the new rates. The IPPR justifies this with illustrative calculations showing gambling companies worsening their odds to maintain their profits. But there’s a point beyond which gambling companies can’t do that, and the IPPR’s proposal may go well past this point.

If the IPPR are wrong, and the tax can’t be passed on, then the revenues raised would be much less than £3bn – potentially half.

This is always the problem with “sin taxes”. We can use them to raise revenue. We can use them to deter the “sin”. But we need to be clear what we’re trying to achieve. And we need to be honest and admit that most of the tax is realistically paid by the sinners, not the companies selling the sin.

The proposal

The UK has a confusing array of different taxes on gambling. The IPPR paper proposes large increases in the most important ones:

Remote gaming duty increased from 21% to 50%. This applies to online gaming supplied to UK customers, wherever in the world the supplier is, and is expected to raise about £1.1bn this year.

Machine gaming duty increased from 20% to 50%. MGD applies to e.g. fruit machines, quiz machines, and fixed odd betting terminals. The tax raises about £600m this year.

General betting duty increased from 15% to 25%. This applies to sports betting and most other gambling (except horse racing, which already pays an additional 10% levy). The tax raises around £700m.

The £2.4bn raised by these taxes would increase to about £5.6bn. This would probably be the rare case of a popular tax increase – Portland Communications found that, if they asked the public which taxes should be increased, gambling taxes topped the table.

In many cases we’d expect so large an increase in tax to reduce the gambling companies profits and, as these taxes apply to profits, result in only a small increase in revenue – or even a decrease in revenues (a “Laffer curve” effect). However, previous increases in gambling taxation have not had this effect: the rate of remote gaming duty went up by 40% from April 2019, and the result was a 33% increase in revenue.

That suggests there is potential to raise gambling taxes and raise revenue – but the IPPR’s increase is much larger – up to 138% for remote gaming duty. It therefore can’t just be assumed that history is a guide to what will happen. So it’s disappointing that the £3bn estimate is “static” – it doesn’t take account of “Laffer” effects. Instead, the IPPR justify the figure through an illustrative calculation.

The IPPR’s illustrative calculation, and what it means

The IPPR’s report says:

“It is only fair, therefore, that these companies, which are exempt from any form
of VAT and often based overseas, contribute more to help wider social aims
where they can – and the industry is booming.“

I think the reader would assume from this that it’s the gambling companies who end up paying the tax. That is, however, not necessarily the case. It’s usually thought that gambling companies respond to increases in gambling taxes by passing the cost on to gamblers, in the form of worse odds. Or, as an economist would say, the “legal incidence” of gambling taxes is on gambling companies – they pay the tax to HMRC, but the “economic incidence” of gambling taxes largely falls on gamblers.

The IPPR report relies on this, because it means profits aren’t hit, and so “Laffer” effects are limited:

While behavioural effects should be considered, we agree with the assessment of the Social Market Foundation that previous HMRC commissioned analysis from 2014, which examined the behavioural effects of levy rises, should not be considered as definitive as their conclusions are based on assumptions rather than their own data analysis. Furthermore, we expect that firms will seek to protect their bottom lines by worsening odds. Even if the 2014 analysis is correct and this leads to a smaller market overall, higher margins for firms are likely to lead to higher surplus and strong possibility of higher government revenue through gambling duties than set out in this paper. It is worth noting that gambling markets continue to work well under tax regimes with much higher tax rates than our own.

This approach is justified by an illustrative example which shows how the incidence falling on gamblers means that tax revenues increase, even when the rate rises significantly:

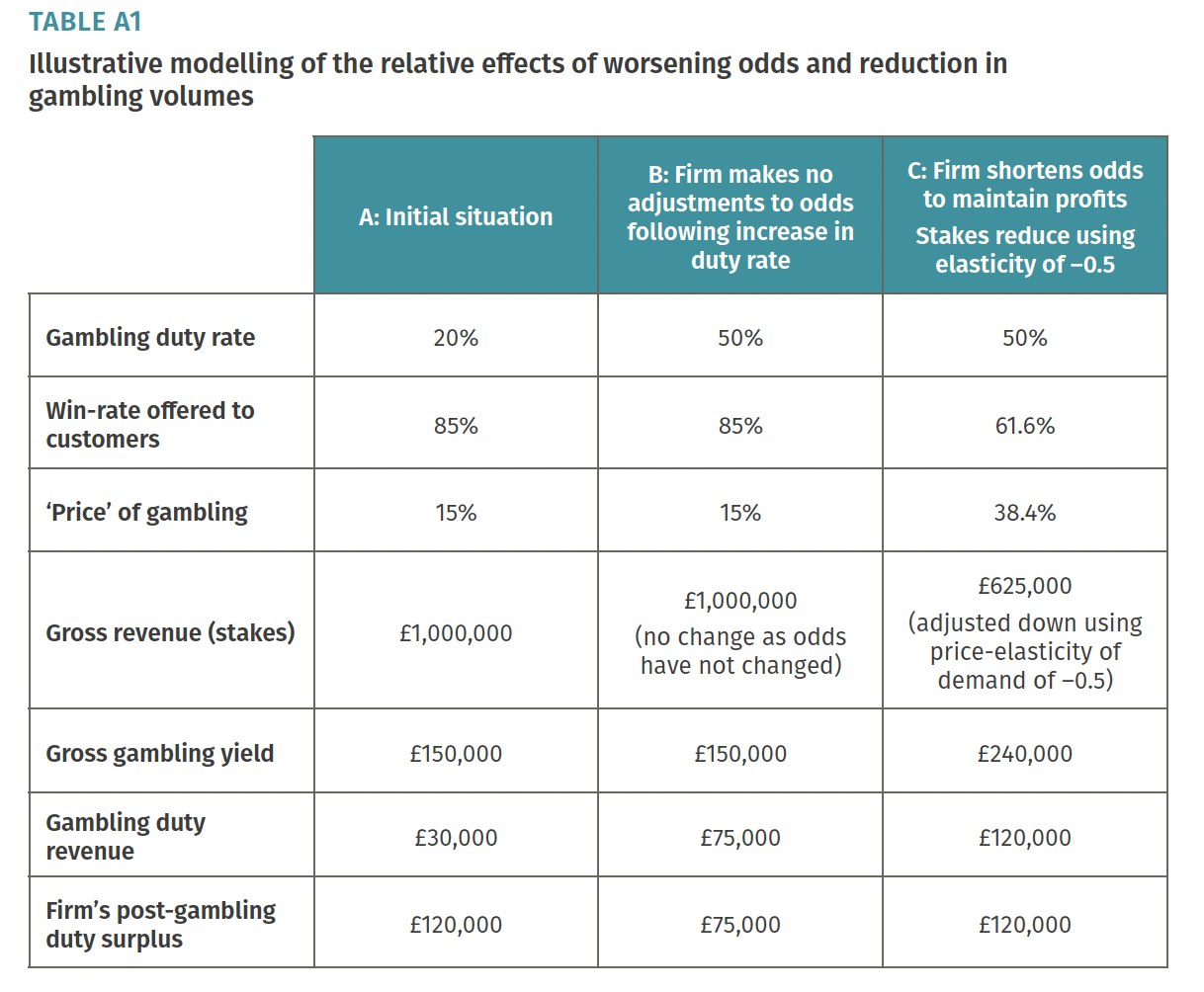
TABLE A1 Illustrative modelling of the relative effects of worsening odds and reduction in gambling volumes A: Initial situation B: Firm makes no adjustments to odds following increase in duty rate C: Firm shortens odds to maintain profits Stakes reduce using elasticity of –0.5 Gambling duty rate 20% 50% 50% Win-rate offered to customers 85% 85% 61.6% ‘Price’ of gambling 15% 15% 38.4% Gross revenue (stakes) £1,000,000 £1,000,000 (no change as odds have not changed) £625,000 (adjusted down using price-elasticity of demand of –0.5) Gross gambling yield £150,000 £150,000 £240,000 Gambling duty revenue £30,000 £75,000 £120,000 Firm’s post-gambling duty surplus £120,000 £75,000 £120,000

The first column is how things are now.

The second column is where the gambling company simply absorbs the increased gaming duty (with its post-tax profit dropping by about 40%).

The third column is what the IPPR thinks will happen: the gambling company protects its margin by worsening odds. Its revenue reduces by 40% but its profit remains the same. The increase in duty has, in economic terms, been entirely paid by gamblers.

This is a simplistic illustrative calculation. I doubt gambling companies would be able to pass all the cost of increased duties to gamblers (particularly for online gaming, where the odds across different platforms serving different countries are very visible).

We should, however, expect a good part of the burden of the tax will economically be borne by gamblers. Whether that is an acceptable outcome is a political question. Personally I find it troubling because, as the IPPR report says:

It is also becoming increasingly apparent that, while many people do gamble, the vast majority of profits derived by gambling firms come from a small number of prolific gamblers. A recent UK study found that the top 10 per cent of online gambling accounts by amount staked account for nearly 80 per cent of operator revenue (NatCen 2022). Previous work from the House of Lords gambling industry select committee found that 60 per cent of the industry’s profits came from just the 5 per cent of customers who were either problem gamblers or at risk (HoL 2020).

And there is evidence from a Finnish study that the incidence of gambling tax may be particularly focussed on lower income gamblers.

What happens if the IPPR are wrong?

The figure in the IPPR’s illustrative table is based upon a “price elasticity of demand” of -0.5. In other words, that a 10% increase in the “price” of gambling (the odds) will result in a 5% decrease in the gambling revenue. This is a large effect, but IPPR’s illustrative figures show that gambling companies can (in principle) still protect their margins by worsening odds, and so making a greater percentage profit from that reduced revenue.

However there is a point where this stops working.

As the price elasticity rises beyond -0.5, gambling firms have to make the odds worse and worse to keep their margins. But there’s a limit – eventually the odds become impossible.

Here’s what happens if we add a column D to the IPPR’s table, with elasticity of -0.75:1

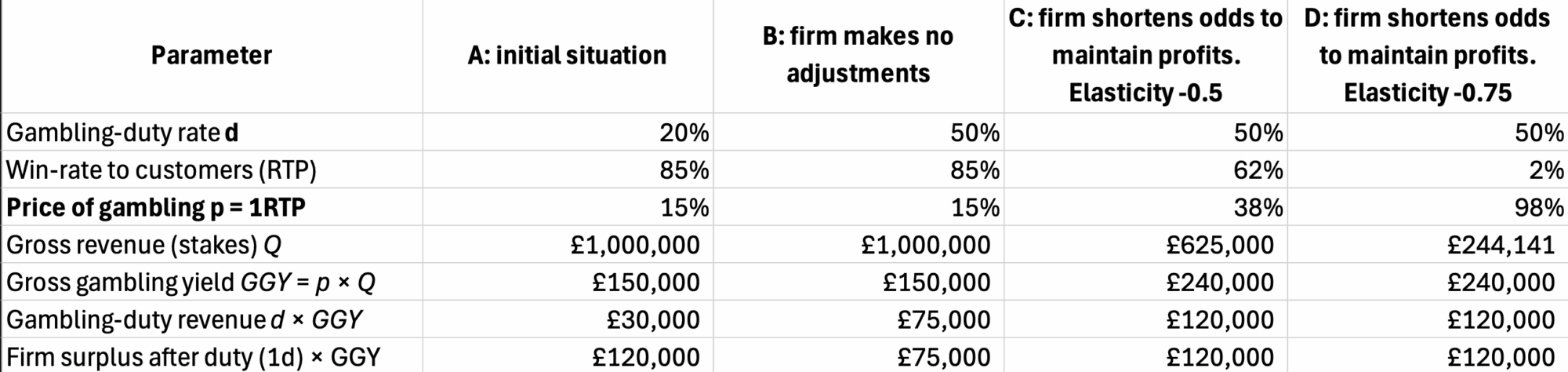
Parameter A: initial situation B: firm makes no adjustments C: firm shortens odds to maintain profits. Elasticity -0.5 D: firm shortens odds to maintain profits. Elasticity -0.75 Gambling‑duty rate d 20% 50% 50% 50% Win‑rate to customers (RTP) 85% 85% 62% 2% Price of gambling p = 1RTP 15% 15% 38% 98% Gross revenue (stakes) Q £1,000,000 £1,000,000 £625,000 £244,141 Gross gambling yield GGY = p × Q £150,000 £150,000 £240,000 £240,000 Gambling‑duty revenue d × GGY £30,000 £75,000 £120,000 £120,000 Firm surplus after duty (1d) × GGY £120,000 £75,000 £120,000 £120,000

At that point, margins can only be maintained if customers’ win-rate drops from 85% (as at present) to 2%. It’s unlikely anyone would gamble in such a scenario. And beyond -0.75, it becomes impossible to maintain margins with this strategy.

Gambling companies could, in principle, take the opposite approach, and maintain their margins by greatly increasing sales. It’s unclear if that’s possible, but I expect most people would consider it an undesirable outcome.

So the IPPR’s simple “illustrative” approach only makes sense if its estimate of a -0.5 elasticity is roughly correct. Beyond that point, their simple assumption that profits can remain broadly static fails, and a more complex analysis is required.

The calculation above is absolutely not a proper analysis – it merely identifies an important limitation of the IPPR’s illustrative calculation. There are numerous real-world factors which complicate matters,2 and the real-world limit of the IPPR’s approach will not be -0.75 – a detailed analysis would be required to determine where it lies.

Is -0.5 the correct figure?

HMRC published a report by Frontier Economics in 2014 showing high elasticities, particularly for remote gaming duty: up to -1.8.

Earlier this year, the Social Market Foundation published a proposal to increase gambling taxes (more modestly than the IPPR’s proposal). The SMF were critical of the figures in the HMRC report, saying that much of it rests upon questionable assumptions rather than empirical evidence. The IPPR say they agree with the SMF.

The HMRC and SMF documents are both serious and considered pieces of work, and I and our team have not assessed the merits of the two positions.

But the point is of critical importance to the IPPR paper. if the HMRC/Frontier figures were correct then, applying the -1.8 (rather than -0.5) elasticity to IPPR’s numbers cuts the extra remote gaming duty revenue by about two-thirds. Because RGD is the single biggest component of the £3bn package, that alone would mean the whole yield would fall to about £1.5bn – half the expected £3bn.

Given the dependence on the -0.5 figure, it is therefore unfortunate that the IPPR present only one scenario. It would be preferable to admit the uncertainty and discuss the range of possible outcomes.

Conclusion

We need to be careful about trying to raise additional revenue from “sin” taxes. The revenue may be less than we expect, and what revenue we do receive may (in economic terms) come from customers rather than the businesses making the sale.

Personally I see compelling arguments for reducing the harms caused by gambling; but I’m unconvinced tax is a good tool for doing that. Regulation may be a better approach.

A tax increase may still be worth doing as a revenue-raiser. But any argument for an increase needs a more robust revenue estimate than the IPPR’s use of a static calculation and illustrative tables. And it needs to acknowledge who is actually paying the price.

Thanks to H for a discussion on elasticities and help with the modelling.