Quantum computing holds the potential to revolutionise computation, but current quantum devices face limitations in terms of resources and stability. Tobias Fischbach, Pierre Talbot, and Pascal Bourvry from the University of Luxembourg present a comprehensive review of quantum circuit optimisation using ZX-calculus, a powerful mathematical framework that allows for the manipulation of quantum circuits while preserving their meaning. Their work categorises existing optimisation techniques, considering factors such as performance metrics and the specific quantum computing architecture targeted, and provides a valuable resource for researchers in both quantum computing and combinatorial optimisation. By clarifying the landscape of ZX-based optimisation, this review highlights critical challenges and outlines promising avenues for future research, including the development of more efficient algorithms and improved methods for translating optimised circuits into physical implementations.
ZX-Calculus Optimizes Quantum Circuit Complexity
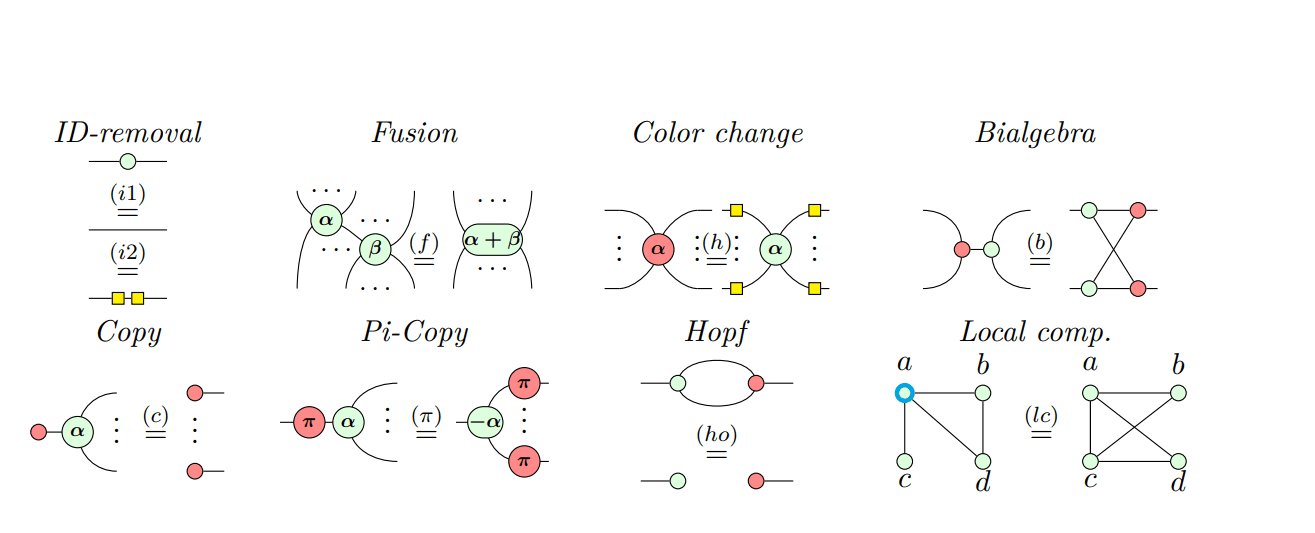
This research explores the application of ZX-calculus, a formal language and powerful framework, to optimize quantum circuits, moving beyond traditional gate-by-gate manipulation. A primary goal is to reduce the number of gates, particularly expensive T-gates, crucial for improving performance on near-term quantum devices with limited coherence. Researchers are increasingly focusing on optimizing circuits for specific quantum hardware architectures, considering qubit connectivity and gate fidelities. Many approaches represent quantum circuits as polynomials using ZX-calculus, then manipulate these polynomials to achieve optimization, with a growing trend towards automated tools and compilers applying these techniques.
Reinforcement learning and other machine learning techniques are also being explored to learn optimization strategies or guide the search for optimal circuits, alongside optimization of phase polynomials, a key area linked to circuit complexity. Researchers are leveraging patterns from measurement-based quantum computation to simplify circuits, establishing a foundation for advanced quantum compilation tools. Expect to see more sophisticated tools and algorithms based on this framework, with a crucial focus on architecture-aware optimization and the integration of machine learning techniques.
ZX-Calculus Optimizes Noisy Quantum Circuits
This work pioneers a systematic review of quantum circuit optimization techniques using ZX-calculus, a graph-based framework offering advantages over traditional gate manipulation. Researchers formally introduce quantum circuits, explaining their composition of qubits and quantum gates, the fundamental units of quantum information processing. The study distinguishes between architecture-independent and architecture-dependent optimization strategies, highlighting that reducing circuit depth speeds up computation while minimizing noisy gates lessens the burden on error correction. Architecture-dependent optimization considers the specific characteristics of quantum hardware, tailoring the circuit to the device’s topology.
The core innovation lies in the application of ZX-calculus, which represents quantum computations as ZX-diagrams, independent of specific gate sets, allowing for simplification rules beyond the gate level. Scientists demonstrate how ZX-calculus enables optimizations for both current and future quantum devices, offering a powerful alternative to conventional methods. The study systematically categorizes existing ZX-based optimization techniques by optimization strategies, target metrics, and architectural dependence, providing a comprehensive overview of the field and identifying key challenges for future research.
ZX-Calculus Optimizes Quantum Circuit Design
This work presents a comprehensive survey of quantum circuit optimization techniques utilizing ZX-calculus, a diagrammatic framework offering a powerful and compact alternative to traditional circuit-level methods. Researchers demonstrate that ZX-calculus enables optimizations beyond those achievable with conventional approaches, positioning it as a versatile intermediate representation for circuit design. The survey categorizes existing techniques, clarifying their strengths and limitations, and provides a valuable resource for both combinatorial optimization and quantum computing specialists. Current adoption of ZX-based methods faces challenges related to scalability, a reliance on single-objective optimization, and the computational cost associated with converting ZX diagrams into quantum circuits.
The research identifies a clear need for future work to expand beyond single-metric optimization, embracing multi-objective approaches that simultaneously consider both architecture-independent and architecture-aware metrics. Furthermore, improvements to circuit extraction methods, potentially through the use of surrogate models or composite metrics, are crucial to reduce computational demands. The authors also note that current research disproportionately focuses on certain quantum computing architectures, with trapped-ion, neutral-atom, and photonic devices being comparatively underrepresented, highlighting the need for broader exploration.