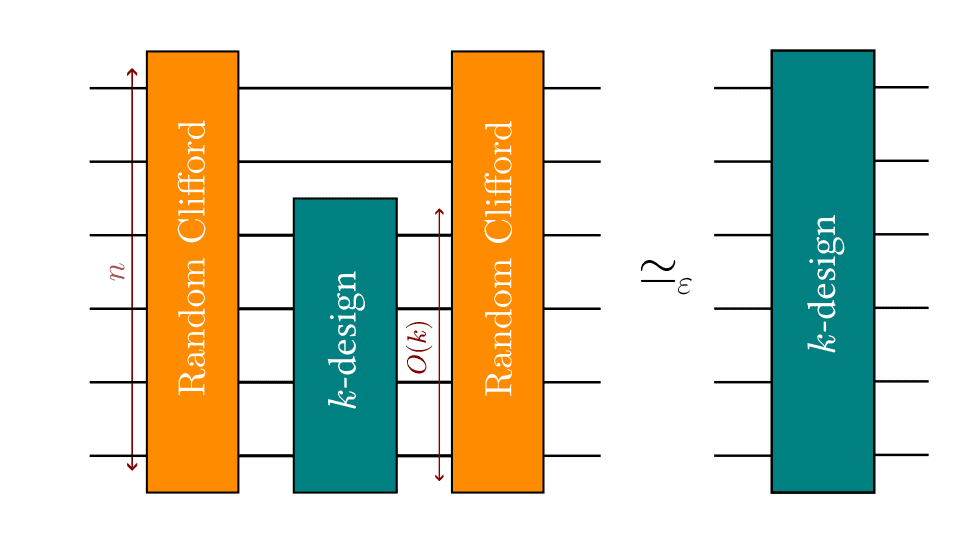Randomness forms a cornerstone of modern information technologies, driving advances in algorithms and error correction, but creating truly random processes demands significant resources. Lennart Bittel from Freie Universität Berlin and Lorenzo Leone from the Università degli Studi di Salerno, along with their colleagues, now present a new protocol called Homeopathy that generates highly random quantum processes with a dramatically reduced need for complex operations. Inspired by the principles of homeopathy, their method applies a small amount of true randomness to a limited part of a quantum system, then effectively ‘dilutes’ it across all the quantum bits. This innovative approach achieves a level of security against even the most sophisticated attacks while simultaneously lowering the operational cost, bringing high-order random processes closer to practical realisation in future quantum computers and potentially unlocking significant advancements in quantum technologies.
Constructing Random Unitaries With Non-Clifford Gates
Scientists have developed a new method for creating random quantum operations, crucial for secure quantum computation and advanced algorithms. This approach, termed Quantum Homeopathy, constructs unitary k-designs, sets of operations mimicking truly random ones, while minimizing the use of complex non-Clifford gates. The technique applies a foundational k-design to a small group of quantum bits, then effectively “diluting” it across the entire system using random operations. This dilution process creates a system indistinguishable from a truly random one, even though it begins with a limited, structured design.
The research demonstrates that this construction requires only a minimal number of non-Clifford gates, achieving quantum-polynomial security, meaning it remains secure against any quantum algorithm running for a reasonable amount of time. Importantly, the method can be implemented with shallow circuit depth, making it practical for near-term quantum computers with limited capabilities. This achievement reduces the resource demands for building quantum-secure systems, offering a pathway to more efficient and scalable quantum technologies. By minimizing the number of non-Clifford gates, this work provides a solid foundation for building secure quantum algorithms and protocols, paving the way for more robust and reliable quantum computation. In essence, this research offers a way to create seemingly random quantum operations starting with a small, well-defined system and expanding it with carefully chosen random operations. By optimizing this process, scientists can minimize the complexity of the required operations, making secure quantum computation more accessible and practical.
Homeopathic k-Designs with Reduced Gate Count
Scientists have pioneered a new protocol, termed Quantum Homeopathy, to generate random quantum operations, known as unitary k-designs, on quantum bits. This method significantly reduces the number of costly non-Clifford gates required for implementation. The technique applies a k-design to a small subsystem, independent of the total number of quantum bits, and then “dilutes” it across the entire system using random operations, creating a highly accurate approximation of a truly random operation. The team rigorously proved that this construction delivers full security against even the most sophisticated quantum attacks, utilizing a minimal number of non-Clifford gates.
They demonstrated that for security against standard quantum algorithms, the number of required gates is further reduced, establishing a lower bound on the number of non-Clifford gates needed to achieve this level of security. This advancement addresses a central limitation in building practical quantum computers, where non-Clifford gates are the most expensive and challenging components. By minimizing the number of these gates, this research makes high-order unitary designs attainable in near-term fault-tolerant quantum architectures, paving the way for more efficient and scalable quantum technologies.
Homeopathy Generates Secure Random Quantum Operations
Scientists have achieved a breakthrough in generating random quantum operations, essential for applications ranging from secure communication to advanced quantum simulations. This new method, termed “Homeopathy,” constructs unitary k-designs on quantum bits with a minimal number of non-Clifford gates, significantly reducing the resource demands of near-term quantum computers. The technique involves applying a k-design to a small group of quantum bits and then “diluting” it across the entire system using random operations, creating a highly accurate approximation of a truly random operation. The team proved that this new method achieves full security against even the most powerful quantum attacks, utilizing a minimal number of non-Clifford gates. Measurements confirm that for security against standard quantum algorithms, the number of required gates is further reduced, representing a substantial improvement over existing approaches. The research demonstrates the construction of “quantum-secure” k-designs using a minimal number of non-Clifford gates, making high-order unitary designs practically attainable, and enabling more complex and powerful quantum computations.
System-Size Independent Unitary Designs Demonstrated
Scientists have presented a new method for constructing random quantum operations, known as unitary designs, with a minimal number of non-Clifford gates. This new method, termed Homeopathy, applies a design to a small subsystem of quantum bits and then “dilutes” it across the entire system using random operations, achieving a full, secure design. This approach significantly reduces the number of complex non-Clifford gates required for implementation. The key achievement lies in demonstrating that this diluted design requires only a system-size-independent number of non-Clifford gates, a substantial improvement over previous approaches that scaled with the number of quantum bits.
The researchers proved this construction achieves security against even the most powerful quantum attacks, and further demonstrated that security against standard quantum algorithms can be achieved with an even lower gate count. This advancement makes the practical implementation of high-order unitary designs feasible on near-term quantum computers, paving the way for more efficient and scalable quantum technologies. The research offers a conceptually new approach to unitary design construction, demonstrating that security against any quantum measurement can be achieved with a minimal number of non-Clifford gates.