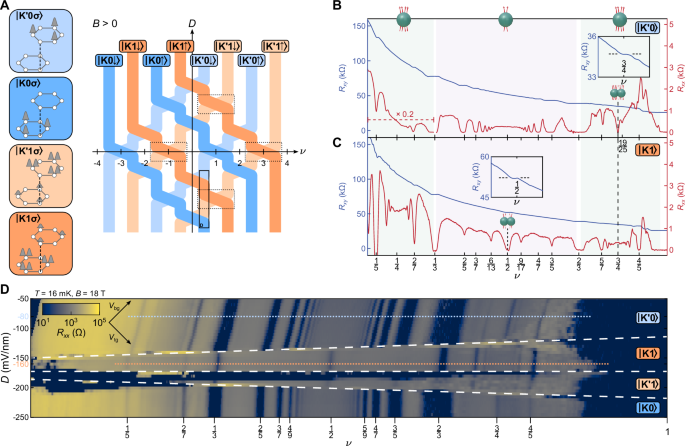
Our devices (device 1 and device 2) consist of BLG encapsulated by hexagonal boron nitride (hBN) and graphite layers acting as gates49; see Methods section. Subsequently, we fabricated the heterostructures into a Hall bar, as shown in supplementary note 1. The electrical transport properties of device 1 were measured in a dilution refrigerator with a base temperature T = 16mK and a magnetic field B up to 18T. Device 2 was measured in another dilution refrigerator with a base temperature T = 10mK and a magnetic field up to 12T. The data shown in the main manuscript are from device 1 and are consistent with those of device 2 (see supplementary note 12). Using a standard low-frequency lock-in technique, we measured the longitudinal (Rxx) and transverse (Rxy) resistances; see supplementary note 1. Subsequently, fully developed FQH states were identified according to their Rxy values and accompanying minima in Rxx. For less developed plateaus, the filling factors were determined by the position of their Rxx minima with respect to fully developed plateaus, e.g., \(\frac{2}{5}\), \(\frac{1}{2}\), and \(\frac{3}{5}\), etc. The dual-gate geometry permits independent tuning of filling factor ν and displacement field D, thus granting control over both the orbital (N = 0, 1) and the valley isospin (K, \({K}^{{\prime} }\))18,44.
Figure 1B shows Rxx and Rxy as a function of ν at D = −80 mV/nm and B = 18T, where the integer LL has an N = 0 orbital. We observe a compressible 2CF metal at \(\nu=\frac{1}{2}\), flanked by an abundance of SdH oscillations, testifying to the low disorder of the device. As we increase the displacement field to D = −160 mV/nm, the LL transitions to N = 1. Here, we observe an incompressible state at \(\nu=\frac{1}{2}\) and a strong suppression of the Jain states; see Fig. 1C. The diminished Rxx along with a quantized plateau in Rxy indicates pairing of 2CFs at \(\nu=\frac{1}{2}\). Surprisingly, near \(\nu=\frac{3}{4}\), the roles of N = 0 and N = 1 are reversed: For N = 0, we observe a strong suppression of Rxx along with a plateau in Rxy at \(\nu=\frac{3}{4}\), indicating the pairing of 4CFs. By contrast, at N = 1, this filling hosts a compressible 4CF metal flanked by SdH oscillations. Fig. 1D shows Rxx over a continuous range of ν and D, which confirms the robustness of both half- and quarter-filled states. Moreover, it shows that these states form irrespective of the valley isospin (see supplementary note 4 Fig. 9). The quarter- and half-filled states at \(\nu=\frac{3}{4}\) and \(\nu=\frac{1}{2}\) were also observed in device 2, see supplementary note 12. Consistent with previous studies18,22, which reported a slope of 2 × 10−4 \(\frac{1}{{{{\rm{mV/nm}}}}}\) in the minima of Rxx within the ν–D phase space, our observation revealed a slope of approximately \(3\times 1{0}^{-4}\frac{1}{{{{\rm{mV/nm}}}}}\). These slopes are most likely due to changes in quantum capacitance, which changes with displacement field (see supplementary note 4 for more discussion on this point).
We now broaden our study to all eight levels comprising the zero-energy LL. In Fig. 2A, we show Rxx as a function of ν and D for the hole-doped (left) and electron-doped (right) sides. Dark-blue areas mark Rxx < 10Ω where the bulk becomes incompressible. On the hole (electron) side, the Rxx measurement is overshadowed by artifacts for negative (positive) D due to the contact fabrication scheme; see Methods section. We observed all previously reported half-filled states at \(\nu=-\frac{5}{2} , -\frac{1}{2} , \frac{3}{2} , \frac{5}{2} , \frac{7}{2}\) along with the same daughter states22. All theoretically predicted daughter states occur at filling factors that coincide with the Jain sequence \({\nu }_{{{{\rm{Jain}}}}}=\frac{n}{2n+1}\) for relatively large ∣n∣. However, the gaps of the Jain sequence are expected to decrease as \(\Delta \sim \frac{1}{2n+1}\) toward half filling, consistent with observations in N = 0 LLs16,50. We identify anomalously strong states that violate this pattern as daughter states, by comparing the strength of the Rxx minima. For example, in Fig. 1C, we observe Jain states only up to n = 3 (\(\nu=\frac{3}{7}\)) on the particle-like side and down to n = −4 (\(\nu=\frac{4}{7}\)) on the hole-conjugate side. This observation strongly suggests that the prominent states at n = 6 (\(\nu=\frac{6}{13}\)) and n = − 9 (\(\nu=\frac{9}{17}\)) have a fundamentally different character, i.e., they are daughter states.
Fig. 2: Even-denominator FQH states in the zero-energy LL of BLG.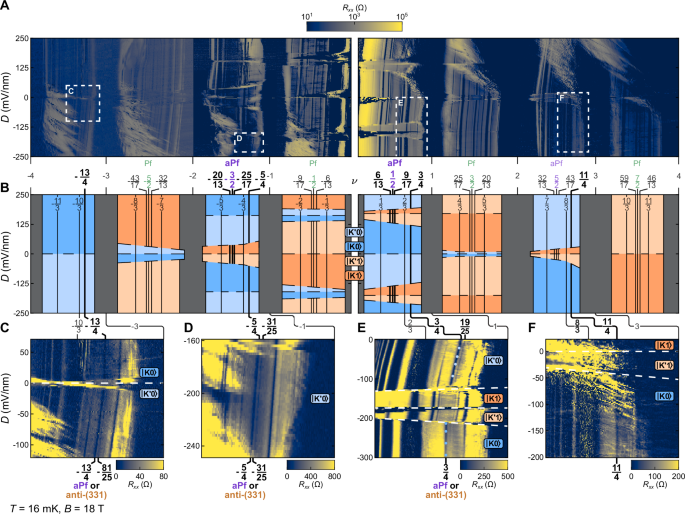
A Rxx as a function of ν and D for − 4≤ν < 0 (left panel) and 0 < ν≤4 (right panel). Areas highlighted by dashed boxes refer to high-resolution measurements in (C–F). See supplementary note 4 for enlarged view. B Schematic summary of all even- and selected odd-denominator FQH states observed in (A), with higher-order Jain states omitted to increase visibility. Vertical lines mark observed FQH states; bold vertical lines mark FQH states at half- and quarter fillings that were not observed in previous works18,19,22. Dashed lines mark valley and orbital crossings along the ν–D phase space. Green and purple labels indicate Pfaffian (Pf) and anti-Pfaffian (aPf) states, respectively, according to their Levin–Halperin daughters. C–F Rxx measurements near the four quarter-filled states. Blue dots in (E) mark the values of D where we measured the gap \({\Delta }_{\frac{3}{4}}\) in Fig. 4E.
The half-filled state at \(\nu=-\frac{3}{2}\) emerges in a single pocket around D = 0, accompanied by daughter states at \(\nu=-\frac{20}{13} , -\frac{25}{17}\) (see supplementary note 10 Fig. 21). The one at \(\nu=\frac{1}{2}\) occurs in two pockets centered around D = ±170 mV/nm, with daughters at \(\nu=\frac{6}{13} , \frac{9}{17}\). All half-filled states develop only at N = 1, where the Jain states are strongly suppressed, and quarter-filled states are absent.
Upon tuning the orbital index from N = 1 to N = 0, we observed quarter-filled states at \(\nu=\frac{3}{4}+(-4 , -2 , 0 ,+2)\) and a suppression of the 4CF Jain sequences around these fillings. This observation is consistent with previous studies in GaAs28,29,30,32,51. Here, quarter-filled states in hole-doped systems were attributed to LLM, estimated to be \(\frac{{E}_{{{{\rm{C}}}}}}{\Delta }\approx 3-8\), where EC is the Coulomb energy and Δ is the cyclotron energy. The estimated LLM in BLG is similar, i.e., \(\frac{{E}_{{{{\rm{C}}}}}}{{\Delta }_{01}}\approx 5-10\), with Δ01 the gap between the N = 0, 1 levels of the same spin and valley,19 and could therefore promote 4CF pairing. More importantly, we observe their daughter states at \(\nu=\frac{9}{25}+(-4 , -2 , 0)\); see Fig. 2C–F, which we use to constrain their topological order. The systematic appearance of these states in every second LL in BLG along with identical daughters suggests a common origin.
In Fig. 2B, we summarize the observed quarter- and half-filled states along with their daughter states, highlighting their dependence on the orbital and valley isospin indices. The half- and quarter-filled states that were not observed in previous works18,19,22, are shown by bold, solid black lines; see supplementary Figs. 11 and 12 for an enlarged view of hole and electron side along with their schematics. We already labeled the even-denominator states according to their identification via Levin–Halperin daughter states and in-plane B measurements, which we discuss below.
We proceed with a detailed characterization of all half-filled states. To avoid ambiguity, we identify all states according to the topological phase of the electrons for either sign of ν. In Fig. 3A, we show the filling factors of daughters associated with different pairing channels of 2CFs38,39. In Fig. 3B, we show Rxx and Rxy around \(\nu=\frac{1}{2}\) at D = −140 mV/nm, with strong dips in Rxx flanking the plateau at half filling. The absence of higher-order Jain states beyond \(\nu=\frac{2}{5} , \frac{3}{5}\) suggests that the dips near \(\nu=\frac{1}{2}\) are daughter states. We mark possible daughter-state fillings by vertical dashed lines with their colors referring to the topological order of the parent state from Fig. 3A, including Pf and anti-Pfaffian favored by numerics3 and PH-Pfaffian suggested by thermal conductance measurements in GaAs52,53,54. The observed dips coincide with \(\frac{6}{13}\) and \(\frac{9}{17}\) (see supplementary note 9 for quantization of daughters), supporting anti-Pfaffian pairing for \(\nu=\frac{1}{2}\). Similarly, based on the daughters, we identified the state at \(\nu=-\frac{3}{2}\) to be anti-Pfaffian (supplementary note 10). Our analysis of the other half-filled states and the plateaus of their daughters, which agrees with previous reports,22 is shown in supplementary notes 8 and 9. The identification of paired states based on their daughters is indirect and has not been independently confirmed by direct measurements, such as thermal conductance52,53 or upstream noise at interfaces.54 Still, the periodic pattern of topological orders indicated by daughters38,39 and its systematic association with crossing N = 1 levels (see dotted boxes in Fig. 1A) provides strong support for its veracity.
Fig. 3: Topological orders of half-filled states in BLG.
A Classification of half-filled states and their identification based on daughter-state fillings. The pairing channel ℓ corresponds to the number of Majorana edge channels (see supplementary note 13). B Rxx and Rxy around \(\nu=\frac{1}{2}\), measured at B = 18T and D = −140 mV/nm, along with possible daughter states marked by vertical dashed lines. C The thermal activation gap \({\Delta }_{\frac{1}{2}}\) measured as a function of B∥ at B⊥ = 15T. The dashed line represents the gap value at B⊥ = 15T and B∥ = 0T. D Identification of all observed half-filled states based on their daughters, along with the measured thermal activation gaps. The gap of all the half-filled states was measured at B = 18T, except for \(\nu=-\frac{3}{2}\) which was measured at B = 11.2T.E Rxx around \(\nu=\frac{3}{2}\) measured as a function of B for D = −140 mV/nm.
Figure 3C shows the dependence of the activation gap \({\Delta }_{\nu=\frac{1}{2}}\) on an in-plane magnetic field B∥ at an out-of-plane field of B⊥ = 15T. The activation gap of the states examined in the manuscript is determined from the slope of the linear fit to the Arrhenius plot of Rxx versus temperature. The error bars reflect the uncertainty in this linear fit (see supplementary note 7 for more details). This method of determining the activation gap and its associated error bar is applied to all figures and tables in the manuscript. We observe negligible variations of \({\Delta }_{\frac{1}{2}}\) up to the largest accessible value of B∥ = 10T, which corresponds to a Zeeman energy of ~14K, more than an order of magnitude larger than \({\Delta }_{\frac{1}{2}}\), similar to previous work18. We, therefore, conclude that the \(\nu=\frac{1}{2}\) state is fully spin-polarized, as expected for the anti-Pfaffian. Note that, to fully validate the spin polarization, a direct approach, such as NMR study is required55,56. A detailed characterization of \(\nu=-\frac{3}{2}\) also indicates a spin-polarized state; see supplementary note 10.
We summarize our identification of the half-filled states in the table of Fig. 3D (see supplementary notes 5 and 8 for gap measurements and daughters of other half-filled states). Strikingly, all observed anti-Pfaffians (aPf) occur in a pair with a Pfaffian (Pf) in the vicinity of two crossing N = 1 levels. There is one such crossing for (\(-\frac{3}{2}\),\(-\frac{1}{2}\)), two for (\(\frac{1}{2}\),\(\frac{3}{2}\)), and one for (\(\frac{5}{2}\),\(\frac{7}{2}\)), each exhibiting (aPf, Pf) on both sides of the crossing (see Fig. 1A and supplementary note 1 Fig. 2 for an illustration). This observation suggests that LLM within these pairs is most relevant for determining the topological order at half filling. Pf or anti-Pfaffian are favored by LLM57,58,59, which is opposite for the two members of each pair. In the lower one, electrons can virtually occupy the empty level above; in the upper one, holes can virtually occupy the filled level below. By contrast, the spin and valley isospin appear to play subordinate roles. The largest gap occurred at \(\nu=\frac{3}{2}\). Fig. 3E shows Rxx around this filling as a function of ν and B. The incompressible state at \(\nu=\frac{3}{2}\) persists down to B = 6T, which places half-filled states in BLG within reach of commonly available magnetic-field setups.
Now we turn to a detailed analysis of the quarter-filled states. Similar to their cousins at half filling, quarter states can also exhibit characteristic daughters38, yet to be observed in other systems. In Fig. 4A, we show the filling factors of daughters associated with the main pairing channels. In Fig. 4B, we show Rxx and Rxy around \(\nu=\frac{3}{4}\) with the possible daughter states indicated by dashed lines, with their colors referring to the topological order of the parent state from Fig. 4A. The line at \(\nu=\frac{19}{25}\) shows remarkable agreement with our data, thereby suggesting the \(\nu=\frac{3}{4}\) topological order to be the non-Abelian anti-Pfaffian or the Abelian anti-(331). The absence of the daughter state to the left of \(\nu=\frac{3}{4}\) is currently unclear and remains a subject of future investigation. To determine the spin polarization of the \(\nu=\frac{3}{4}\) state, we measured its gap while varying B∥ at B⊥ = 15T; see Fig. 4C and supplementary note 7 for more details. The weak dependence of \({\Delta }_{\frac{3}{4}}\) on B∥ up to a Zeeman energy of ~14K again indicates a fully spin-polarized state. In conjunction with the observed daughter state, this observation supports the non-Abelian aPf ground state, as the spin-singlet anti-(331) state should not be spin-polarized60. However, a valley-singlet anti-(331) state remains possible.
Fig. 4: Quarter-filled states in BLG.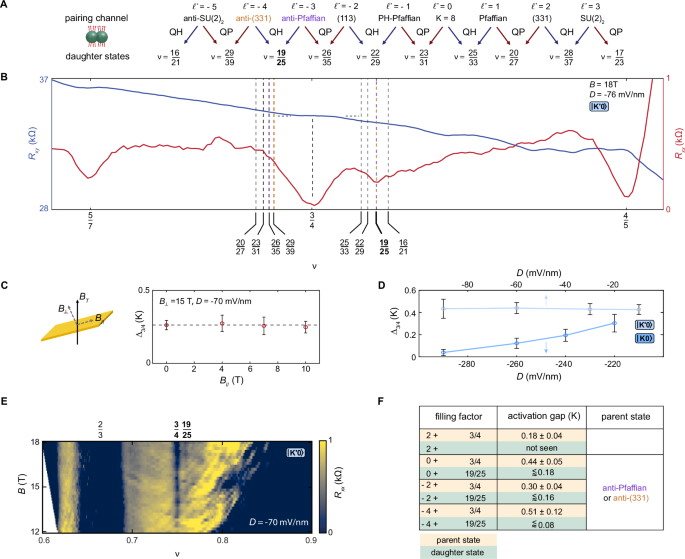
A Classification of quarter-filled states and their identification based on daughter-state fillings. The pairing channel ℓ corresponds to the number of Majorana edge channels (see supplementary note 13). B Rxx and Rxy around \(\nu=\frac{3}{4}\) measured at D = −76 mV/nm, along with possible daughter states marked by vertical dashed lines. C The thermal activation gap of \(\nu=\frac{3}{4}\) measured as a function of B∥ at B⊥ = 15T. The dashed line represents the gap value at B⊥ = 15T and B∥ = 0T. D \({\Delta }_{\frac{3}{4}}\) measured as a function of D in different valleys. E Rxx around \(\nu=\frac{3}{4}\) measured as a function of B for D = −70 mV/nm. F Constraints on the ground states of all observed quarter-filled states based on their daughters, along with the measured thermal activation gaps.
To probe the valley polarization, we measured \({\Delta }_{\frac{3}{4}}\) as a function of D; see Fig. 4D and supplementary note 6 for more details. For the \({K}^{{\prime} }\) valley, we find that the gap remains constant as the absolute value of D increases. By contrast, in the K valley, the gap decreases monotonically. However, this behavior does not necessarily imply a valley singlet state. Indeed, a reduction of the gap with D was also reported for \(\nu=\frac{3}{2}\)18. There, the gap eventually saturates to a non-zero value, and a single-component state is further supported by the daughters22. Consequently, our measurement can neither rule out an anti-Pf nor a valley-singlet anti-(331) state. Fig. 4E shows Rxx as a function of ν and B, with the incompressible state at \(\nu=\frac{3}{4}\) persisting down to B = 12T. We summarize our analysis of all observed quarter-filled states and their daughters in the table of Fig. 4F (see supplementary notes 5 and 8 for gap measurements and daughters of other quarter-filled states).
Finally, we have also observed ‘next-generation’ FQH states previously unseen in BLG which are not captured by weakly interacting CFs32,48,61,62,63. Namely, we observed the odd-denominator states \(\nu=\frac{4}{11}\) and \(\nu=\frac{6}{17}\) and the even-denominator state \(\nu=\frac{3}{8}\); see supplementary note 11 for details.