Bayesian continual learning and forgetting in neural networks

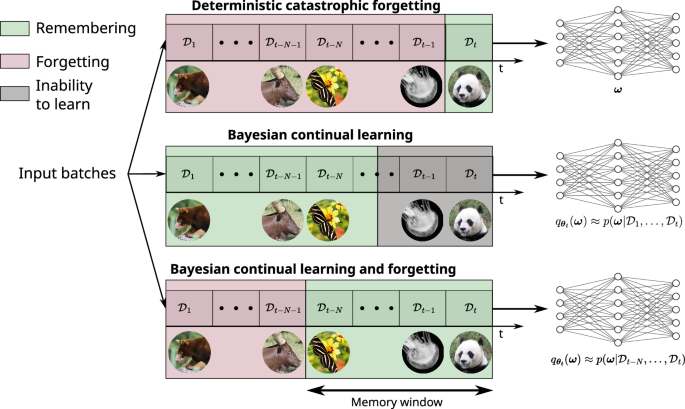
Description of the variational inference framework

Exact computation of the truncated posterior (Eq. (4)) becomes intractable as the number of parameters in the network grows, necessitating approximation methods. Here, we use variational inference (VI), which tackles this challenge by restricting the posterior to a parameterized distribution, known as the variational distribution. We choose a multivariate Gaussian \({q}_{{{\boldsymbol{\theta }}}_{t}}({\boldsymbol{\omega }})\).

To reduce complexity, we adopt the mean-field approximation40, modeling each synaptic weight as an independent Gaussian:

$${q}_{{{\boldsymbol{\theta }}}_{t}}({\boldsymbol{\omega }})=\mathop{\prod }\limits_{i=1}^{s}{q}_{{\theta }_{t,i}}({\omega }_{i})\Rightarrow {q}_{{{\boldsymbol{\theta }}}_{t}}({\boldsymbol{\omega }})={\mathcal{N}}({\boldsymbol{\omega }};{{\boldsymbol{\mu }}}_{t},{\rm{diag}}({{\boldsymbol{\sigma }}}_{t}^{2})),$$

where s is the total number of synapses, and each ωi is modeled by \({q}_{{\theta }_{t,i}}({\omega }_{i})={\mathcal{N}}({\omega }_{i};{\mu }_{i},{\sigma }_{i}^{2})\). Our goal is for \({q}_{{{\boldsymbol{\theta }}}_{t}}({\boldsymbol{\omega }})\) to approximate the true truncated posterior \(p({\boldsymbol{\omega }}\,| \,{{\mathcal{D}}}_{t-N},\ldots,{{\mathcal{D}}}_{t})\).

Following standard VI practice9,18,41,42,43, we minimize the Kullback–Leibler (KL) divergence between \({q}_{{{\boldsymbol{\theta }}}_{t}}({\boldsymbol{\omega }})\) and the target posterior:

$${\boldsymbol{\theta}}_t \, =\, \arg\min_{{\boldsymbol{\theta}}} \; D_{KL}\!\left[ q_{{\boldsymbol{\theta}}}({\boldsymbol{\omega}}) \;\|\; p\bigl({\boldsymbol{\omega}}\!\mid\!{\mathcal{D}}_{t-N},\ldots,{\mathcal{D}}_{t}\bigr) \right].$$

(20)

Variational free energy

Starting from Eq. (20), we rewrite the target posterior \(p({\boldsymbol{\omega }}\,| \,{{\mathcal{D}}}_{t-N},\ldots,{{\mathcal{D}}}_{t})\) using Bayes’ rule:

$$p({\boldsymbol{\omega }}\,| \,{{\mathcal{D}}}_{t-N},\ldots,{{\mathcal{D}}}_{t})=\frac{p({{\mathcal{D}}}_{t}\,| \,{\boldsymbol{\omega }})\,p({\boldsymbol{\omega }}\,| \,{{\mathcal{D}}}_{t-N-1},\ldots,{{\mathcal{D}}}_{t-1})}{p({{\mathcal{D}}}_{t})}\times \frac{p({{\mathcal{D}}}_{t-N-1})}{p({{\mathcal{D}}}_{t-N-1}\,| \,{\boldsymbol{\omega }})}.$$

Applying the KL divergence definition \(\,{D}_{KL}[Q\,| \,| P]\,=\,{{\mathbb{E}}}_{Q}[\log (Q/P)]\) and ignoring terms independent of θ, we obtain:

$${{\boldsymbol{\theta }}}_{t}= \arg \mathop{\min }\limits_{{\boldsymbol{\theta }}}{{\mathbb{E}}}_{{q}_{{\boldsymbol{\theta }}}({\boldsymbol{\omega }})}\,\left[\log (\frac{{q}_{{\boldsymbol{\theta }}}({\boldsymbol{\omega }})}{p({\boldsymbol{\omega }}\,| \,{{\mathcal{D}}}_{t-N-1},\ldots,{{\mathcal{D}}}_{t-1})})\right.\\ \left.-\log p({{\mathcal{D}}}_{t}\,| \,{\boldsymbol{\omega }})+ \log p({{\mathcal{D}}}_{t-N-1}\,| \,{\boldsymbol{\omega }})\right].$$

(21)

As explained in the main text, we further approximate \(\,p({\boldsymbol{\omega }}\,| \,{{\mathcal{D}}}_{t-N-1},\ldots,{{\mathcal{D}}}_{t-1})\approx {q}_{{{\boldsymbol{\theta }}}_{t-1}}({\boldsymbol{\omega }})\), which yields

$${{\boldsymbol{\theta }}}_{t}= \arg \mathop{\min }\limits_{{\boldsymbol{\theta }}}\left[{D}_{KL}({q}_{{\boldsymbol{\theta }}}({\boldsymbol{\omega }})\,\parallel \,{q}_{{{\boldsymbol{\theta }}}_{t-1}}({\boldsymbol{\omega }}))-{{\mathbb{E}}}_{{q}_{{\boldsymbol{\theta }}}({\boldsymbol{\omega }})}\,[\log p({{\mathcal{D}}}_{t}\,| \,{\boldsymbol{\omega }})]\right.\\ \left.+ {{\mathbb{E}}}_{{q}_{{\boldsymbol{\theta }}}({\boldsymbol{\omega }})}\,[\log p({{\mathcal{D}}}_{t-N-1}\,| \,{\boldsymbol{\omega }})]\right].$$

(22)

Defining the function \({{\mathcal{F}}}_{t}\) (the variational free energy42,43) as:

$${\mathcal{F}}_t \,= \, \underbrace{ D_{KL}\bigl[q_{{\boldsymbol{\theta}}_t}({\boldsymbol{\omega}})\,\|\, q_{{\boldsymbol{\theta}}_{t-1}}({\boldsymbol{\omega}})\bigr] \,-\, {\mathbb{E}}_{q_{{\boldsymbol{\theta}}}({\boldsymbol{\omega}})}\!\bigl[\log p({\mathcal{D}}_t\,\mid\,{\boldsymbol{\omega}})\bigr] }_{{\text{Learning}}} \,\\ +\, \underbrace{ {\mathbb{E}}_{q_{{\boldsymbol{\theta}}}({\boldsymbol{\omega}})}\!\bigl[\log p({\mathcal{D}}_{t-N-1}\,\mid\,{\boldsymbol{\omega}})\bigr] }_{{\text{Forgetting}}},$$

We recover the expression from the main text (Eq. (5)), which explicitly separates the learning term (adapting to the current task) from the forgetting term (downweighting information from older tasks).

Forgetting term approximation

From Eq. (5) in the main text, the main challenge lies in computing the “forgetting” term \(\,{{\mathbb{E}}}_{{q}_{{\boldsymbol{\theta }}}({\boldsymbol{\omega }})}\,[\log p({{\mathcal{D}}}_{t-N-1}| {\boldsymbol{\omega }})]\). For this purpose, we assume each dataset \({{\mathcal{D}}}_{i}\) has equal marginal likelihood, so

$$p({{\mathcal{D}}}_{t-N-1},\ldots,{{\mathcal{D}}}_{t-1}| {\boldsymbol{\omega }})=\mathop{\prod }\limits_{i=t-N-1}^{t-1}p({{\mathcal{D}}}_{i}| {\boldsymbol{\omega }})={[p({{\mathcal{D}}}_{t-N-1}| {\boldsymbol{\omega }})]}^{N},$$

thus weighting each dataset in the memory window equally. Because our variational and prior distributions are Gaussians, this assumption leads to a closed-form expression for the forgetting likelihood.

Lemma 1: Let \({q}_{{\boldsymbol{\theta }}}({\boldsymbol{\omega }})\approx p({\boldsymbol{\omega }}| {\mathcal{D}})\) be a mean-field Gaussian for a BNN, where θ = (μ, σ) and ω = μ + ϵ ⋅ σ, \({\boldsymbol{\epsilon }} \sim {\mathcal{N}}(\overrightarrow{0},{{\bf{I}}}_{s})\). If the prior is \(p({\boldsymbol{\omega }})={\mathcal{N}}({\boldsymbol{\omega }};{{\boldsymbol{\mu }}}_{{\rm{prior}}},{\rm{diag}}({{\boldsymbol{\sigma }}}_{\,\text{prior}\,}^{2}))\), then \(p({\mathcal{D}}| {\boldsymbol{\omega }})\propto {q}_{L}({\boldsymbol{\omega }})={\mathcal{N}}({\boldsymbol{\omega }};{{\boldsymbol{\mu }}}_{L},{\rm{diag}}({{\boldsymbol{\sigma }}}_{L}^{2})),\) and the negative log-likelihood takes a quadratic form: \({\mathcal{L}}({\boldsymbol{\omega }})=\frac{{({\boldsymbol{\omega }}-{{\boldsymbol{\mu }}}_{L})}^{2}}{2\,{{\boldsymbol{\sigma }}}_{L}^{2}}+ \frac{1}{2}\,\log (2\pi \,{{\boldsymbol{\sigma }}}_{L}^{2}),\) where \(\frac{1}{{{\boldsymbol{\sigma }}}^{2}}=\frac{1}{{{\boldsymbol{\sigma }}}_{L}^{2}}+\frac{1}{{{\boldsymbol{\sigma }}}_{\,\text{prior}\,}^{2}}\) and \({\boldsymbol{\mu }}=\frac{{{\boldsymbol{\mu }}}_{L}\,{{\boldsymbol{\sigma }}}_{\,\text{prior}\,}^{2}+{{\boldsymbol{\mu }}}_{{\rm{prior}}}\,{{\boldsymbol{\sigma }}}_{L}^{2}}{{{\boldsymbol{\sigma }}}_{L}^{2}+{{\boldsymbol{\sigma }}}_{\,\text{prior}\,}^{2}}.\)

A full proof of Lemma 1 appears in Supplementary Note 2. It uses Bayes’ rule for Gaussian posteriors and priors to link μL and σL to μ and σ. In our truncated-posterior setting, \(p({{\mathcal{D}}}_{t-N-1}| {\boldsymbol{\omega }})\propto {q}_{{L}_{t-1}}{({\boldsymbol{\omega }})}^{\frac{1}{N}},\) yielding

$${\mathcal{F}}_t \,=\, \underbrace{\left[ D_{KL}\bigl(q_{{\boldsymbol{\theta}}_t}\|\,q_{{\boldsymbol{\theta}}_{t-1}}\bigr) \,+\, {\mathcal{C}}_t \right]}_{{\text{Learning}}} \,+\, \underbrace{\frac{1}{N}\left[ -\,\frac{\bigl({\boldsymbol{\mu}}_t – {\boldsymbol{\mu}}_{L_{t-1}}\bigr)^2}{2\,{\boldsymbol{\sigma}}_{L_{t-1}}^2} \,-\, \frac{{\boldsymbol{\sigma}}_t^2}{{\boldsymbol{\sigma}}_{L_{t-1}}^2} \right]}_{{\text{Forgetting}}},$$

(23)

where \({{\mathcal{C}}}_{t}=-\,{{\mathbb{E}}}_{{q}_{{{\boldsymbol{\theta }}}_{t}}({\boldsymbol{\omega }})}[\log p({{\mathcal{D}}}_{t}| {\boldsymbol{\omega }})].\) the forgetting term thus “de-consolidates” each synapse, nudging it toward the prior to free capacity for new tasks.

Update rules

To approximate the true posterior distribution at time t, we seek to minimize the free energy \({{\mathcal{F}}}_{t}\). The Kullback–Leibler term in \({{\mathcal{F}}}_{t}\) between two diagonal Gaussians has a known closed form:

$${D}_{KL}[{q}_{{{\boldsymbol{\theta }}}_{t}}({\boldsymbol{\omega }})\parallel {q}_{{{\boldsymbol{\theta }}}_{t-1}}({\boldsymbol{\omega }})]=\mathop{\sum }\limits_{i=1}^{s}\log \left(\frac{{\sigma }_{i,t-1}}{{\sigma }_{i,t}}\right)+ \frac{{\sigma }_{i,t}^{2}+{({\mu }_{i,t-1}-{\mu }_{i,t})}^{2}}{2\,{\sigma }_{i,t-1}^{2}}-\frac{1}{2}.$$

(24)

Taking derivatives of \({{\mathcal{F}}}_{t}\) with regards to μt and σt yields the implicit equations:

$$\frac{\partial {{\mathcal{F}}}_{t}}{\partial {{\boldsymbol{\mu }}}_{t}} = \frac{\Delta {\boldsymbol{\mu }}}{{{\boldsymbol{\sigma }}}_{t-1}^{2}}+ \frac{\partial {{\mathcal{C}}}_{t}}{\partial {{\boldsymbol{\mu }}}_{t}}-\frac{{{\boldsymbol{\mu }}}_{t}-{{\boldsymbol{\mu }}}_{{L}_{t-1}}}{N\,{{\boldsymbol{\sigma }}}_{{L}_{t-1}}^{2}}= \overrightarrow{0},$$

(25)

$$\frac{\partial {{\mathcal{F}}}_{t}}{\partial {{\boldsymbol{\sigma }}}_{t}}=-\,\frac{1}{{{\boldsymbol{\sigma }}}_{t-1}+\Delta {\boldsymbol{\sigma }}}+ \frac{{{\boldsymbol{\sigma }}}_{t-1}+\Delta {\boldsymbol{\sigma }}}{{{\boldsymbol{\sigma }}}_{t-1}^{2}}+ \frac{\partial {{\mathcal{C}}}_{t}}{\partial {{\boldsymbol{\sigma }}}_{t}}-\frac{2\,({{\boldsymbol{\sigma }}}_{t-1}+\Delta {\boldsymbol{\sigma }})}{N\,{{\boldsymbol{\sigma }}}_{{L}_{t-1}}^{2}}=\overrightarrow{0},$$

(26)

where Δμ = μt − μt−1 and Δσ = σt − σt−1. Solving these leads to the MESU update rule:

Theorem 1: Consider a stream of data \({\{{{\mathcal{D}}}_{i}\}}_{i=0}^{t}\). Let \({q}_{{{\boldsymbol{\theta }}}_{t}}({\boldsymbol{\omega }})\) be a mean-field Gaussian for a BNN at time t, with θt = (μt, σt) and samples \({\boldsymbol{\omega }}={{\boldsymbol{\mu }}}_{t}+{\boldsymbol{\epsilon }}\cdot {{\boldsymbol{\sigma }}}_{t},{\boldsymbol{\epsilon }}\, \sim \,{\mathcal{N}}(\overrightarrow{0},{\bf{I}})\). Suppose \({q}_{{{\boldsymbol{\theta }}}_{t-1}}({\boldsymbol{\omega }})\approx p({\boldsymbol{\omega }}\,| \,{{\mathcal{D}}}_{t-N-1},\ldots,{{\mathcal{D}}}_{t-1})\), and that each dataset \({{\mathcal{D}}}_{i}\) has equal marginal likelihood. Under a second-order expansion of \({{\mathcal{C}}}_{t}\) around μt−1 and σt−1, and the small-update assumption \(| \frac{\Delta {\sigma }_{i}}{{\sigma }_{i,t-1}}| \ll 1\), the parameter updates become:

$$\Delta {\boldsymbol{\sigma }}=-\frac{{{\boldsymbol{\sigma }}}_{t-1}^{2}}{2}\,\frac{\partial {{\mathcal{C}}}_{t}}{\partial {{\boldsymbol{\sigma }}}_{t-1}}+ \frac{{{\boldsymbol{\sigma }}}_{t-1}}{2\,N\,{{\boldsymbol{\sigma }}}_{\,\text{prior}\,}^{2}}({{\boldsymbol{\sigma }}}_{\,\text{prior}\,}^{2}-{{\boldsymbol{\sigma }}}_{t-1}^{2}),$$

(27)

$$\Delta {\boldsymbol{\mu }}=-{{\boldsymbol{\sigma }}}_{t-1}^{2}\,\frac{\partial {{\mathcal{C}}}_{t}}{\partial {{\boldsymbol{\mu }}}_{t-1}}+ \frac{{{\boldsymbol{\sigma }}}_{t-1}^{2}}{N\,{{\boldsymbol{\sigma }}}_{\,\text{prior}\,}^{2}}({{\boldsymbol{\mu }}}_{{\rm{prior}}}-{{\boldsymbol{\mu }}}_{t-1}).$$

(28)

A full proof (Supplementary Note 4) uses a second-order Taylor expansion to handle the implicit dependence of μt and σt. Under \(| \frac{\Delta {\boldsymbol{\sigma }}}{{{\boldsymbol{\sigma }}}_{t-1}}| \ll 1\), these updates simplify to Eqs. (27)–(28), balancing learning and forgetting in a single, efficient step.

Links with Newton’s method

We have thus far derived MESU by minimizing the KL divergence between a variational posterior qθ(ω) and the (truncated) true posterior \(p({\boldsymbol{\omega }}| {{\mathcal{D}}}_{t-N},\ldots,{{\mathcal{D}}}_{t})\). Here, we show how a similar update can emerge from Newton’s method if we treat the free energy as the loss function to be minimized in a non-continual setting.

Newton’s method states that for a parameter ω inducing loss \({\mathcal{L}}\), the update is \(\Delta {\boldsymbol{\omega }}=-\,\gamma \,{\left(\frac{{\partial }^{2}{\mathcal{L}}}{\partial {{\boldsymbol{\omega }}}^{2}}\right)}^{-1}\,\,\frac{\partial {\mathcal{L}}}{\partial {\boldsymbol{\omega }}},\) where γ is a step size. Let \({\mathcal{F}}\) be the KL divergence between two multivariate Gaussians: a variational posterior \({q}_{{\boldsymbol{\theta }}}({\boldsymbol{\omega }})={\mathcal{N}}({\boldsymbol{\omega }};{\boldsymbol{\mu }},{\rm{diag}}({{\boldsymbol{\sigma }}}^{2}))\) and a true posterior \(p({\boldsymbol{\omega }}| {\mathcal{D}})\). If the true posterior is itself an (approximate) mean-field Gaussian \(\,p({\boldsymbol{\omega }}| {\mathcal{D}})\approx {q}_{{\rm{post}}}({\boldsymbol{\omega }})={\mathcal{N}}({\boldsymbol{\omega }};{{\boldsymbol{\mu }}}_{{\rm{post}}},{\rm{diag}}({{\boldsymbol{\sigma }}}_{\,\text{post}\,}^{2})),\), then

$${\mathcal{F}}={D}_{KL}[{q}_{{\boldsymbol{\theta }}}({\boldsymbol{\omega }})\parallel p({\boldsymbol{\omega }}| {\mathcal{D}})]=\log \left(\frac{{{\boldsymbol{\sigma }}}_{{\rm{post}}}}{{\boldsymbol{\sigma }}}\right)+ \frac{{{\boldsymbol{\sigma }}}^{2}+{({\boldsymbol{\mu }}-{{\boldsymbol{\mu }}}_{{\rm{post}}})}^{2}}{2\,{{\boldsymbol{\sigma }}}_{\,\text{post}\,}^{2}}-\frac{1}{2}.$$

(29)

To find μpost and σpost, we apply Bayes’ rule with a Gaussian prior \(p({\boldsymbol{\omega }})={\mathcal{N}}({\boldsymbol{\omega }};{{\boldsymbol{\mu }}}_{{\rm{prior}}},{\rm{diag}}({{\boldsymbol{\sigma }}}_{\,\text{prior}\,}^{2}))\) and a Gaussian likelihood \(p({\mathcal{D}}| {\boldsymbol{\omega }})\propto {q}_{L}({\boldsymbol{\omega }})={\mathcal{N}}({\boldsymbol{\omega }};{{\boldsymbol{\mu }}}_{L},{\rm{diag}}({{\boldsymbol{\sigma }}}_{L}^{2}))\) (cf. Lemma 1). This yields:

$$\frac{1}{{{\boldsymbol{\sigma }}}_{\,\text{post}\,}^{2}}=\frac{1}{{{\boldsymbol{\sigma }}}_{L}^{2}}+ \frac{1}{{{\boldsymbol{\sigma }}}_{\,\text{prior}\,}^{2}},\qquad {{\boldsymbol{\mu }}}_{{\rm{post}}}=\frac{{{\boldsymbol{\mu }}}_{L}\,{{\boldsymbol{\sigma }}}_{\,\text{prior}\,}^{2}+{{\boldsymbol{\mu }}}_{{\rm{prior}}}\,{{\boldsymbol{\sigma }}}_{L}^{2}}{{{\boldsymbol{\sigma }}}_{L}^{2}+{{\boldsymbol{\sigma }}}_{\,\text{prior}\,}^{2}}.$$

(30)

Substituting these into (29) gives explicit forms for \(\partial {\mathcal{F}}/\partial {\boldsymbol{\mu }}\), \(\partial {\mathcal{F}}/\partial {\boldsymbol{\sigma }}\), and their second derivatives. In particular,

$$\frac{{\partial }^{2}{\mathcal{F}}}{\partial {{\boldsymbol{\mu }}}^{2}}=\frac{1}{{{\boldsymbol{\sigma }}}_{L}^{2}}+\frac{1}{{{\boldsymbol{\sigma }}}_{\,\text{prior}\,}^{2}}=\frac{1}{{{\boldsymbol{\sigma }}}_{\,\text{post}\,}^{2}},\qquad \frac{{\partial }^{2}{\mathcal{F}}}{\partial {{\boldsymbol{\sigma }}}^{2}}=\frac{1}{{{\boldsymbol{\sigma }}}^{2}}+ \frac{1}{{{\boldsymbol{\sigma }}}_{L}^{2}}+ \frac{1}{{{\boldsymbol{\sigma }}}_{\,\text{prior}\,}^{2}}.$$

(31)

Lemma 2: For a mean-field Gaussian qθ(ω) describing a BNN, with ω = μ + ϵ ⋅ σ, \({\boldsymbol{\epsilon }} \sim {\mathcal{N}}(\overrightarrow{0},{{\bf{I}}}_{s})\), the expected Hessian of the negative log-likelihood \({\mathcal{L}}\) satisfies

$${H}_{D}({\boldsymbol{\mu }})={{\mathbb{E}}}_{{\boldsymbol{\epsilon }}}\left[\frac{{\partial }^{2}{\mathcal{L}}}{\partial {{\boldsymbol{\omega }}}^{2}}\right]=\frac{1}{{\boldsymbol{\sigma }}}\frac{\partial {\mathcal{C}}}{\partial {\boldsymbol{\sigma }}},$$

where \({\mathcal{C}}={{\mathbb{E}}}_{{\boldsymbol{\epsilon }}}\,[{\mathcal{L}}({\boldsymbol{\omega }})]\).

By Lemma 2, we have \(\,1/{{\boldsymbol{\sigma }}}_{L}^{2}=(1/{\boldsymbol{\sigma }})\,(\partial {\mathcal{C}}/\partial {\boldsymbol{\sigma }})\), and under N i.i.d. mini-batches, \(\,1/{{\boldsymbol{\sigma }}}_{L}^{2}=(N/{\boldsymbol{\sigma }})\,(\partial {\mathcal{C}}/\partial {\boldsymbol{\sigma }})=N\,{H}_{D}({\boldsymbol{\mu }}).\) applying Newton’s method then yields:

Theorem 2: Let \({q}_{{\boldsymbol{\theta }}}({\boldsymbol{\omega }})={\mathcal{N}}({\boldsymbol{\omega }};{\boldsymbol{\mu }},{\rm{diag}}({{\boldsymbol{\sigma }}}^{2}))\) be a mean-field Gaussian for a BNN, with ω = μ + ϵ ⋅ σ, \({\boldsymbol{\epsilon }} \sim {\mathcal{N}}(\overrightarrow{0},{{\bf{I}}}_{s})\), and with a prior \(p({\boldsymbol{\omega }})={\mathcal{N}}({\boldsymbol{\omega }};{{\boldsymbol{\mu }}}_{{\rm{prior}}},{\rm{diag}}({{\boldsymbol{\sigma }}}_{\,\text{prior}\,}^{2}))\). Given \({\mathcal{D}}\) split into N i.i.d. mini-batches, and defining \({\mathcal{C}}={{\mathbb{E}}}_{{\boldsymbol{\epsilon }}}[{\mathcal{L}}({\boldsymbol{\omega }})]\), a diagonal Newton update for σ and μ with learning rate γ and σ ≈ σpost becomes:

$$\Delta {\boldsymbol{\sigma }}=\frac{\gamma N}{2}\,\left[-\,{{\boldsymbol{\sigma }}}^{2}\,\frac{\partial {\mathcal{C}}}{\partial {\boldsymbol{\sigma }}}+ \frac{{\boldsymbol{\sigma }}}{N\,{{\boldsymbol{\sigma }}}_{\,\text{prior}\,}^{2}}({{\boldsymbol{\sigma }}}_{\,\text{prior}\,}^{2}-{{\boldsymbol{\sigma }}}^{2})\right],$$

(32)

$$\Delta {\boldsymbol{\mu }}=\gamma N\left[-\,{{\boldsymbol{\sigma }}}^{2}\,\frac{\partial {\mathcal{C}}}{\partial {\boldsymbol{\mu }}}+ \frac{{{\boldsymbol{\sigma }}}^{2}}{N\,{{\boldsymbol{\sigma }}}_{\,\text{prior}\,}^{2}}({{\boldsymbol{\mu }}}_{{\rm{prior}}}-{\boldsymbol{\mu }})\right].$$

(33)

A full proof appears in Supplementary Note 4. Notice the close similarity to MESU’s update rules, especially when γ = 1/N. This shows how Bayesian learning (with forgetting) can be viewed through the lens of second-order optimization, linking our framework both to biological synapse models and to Newton’s method in variational inference.

Dynamics of standard deviations in the i.i.d. scenario

We now examine the evolution of each standard deviation σ under an i.i.d. data assumption, isolating its role as an adaptive learning rate. Starting from

$$\Delta {\boldsymbol{\sigma }}=\gamma \left[-\,{{\boldsymbol{\sigma }}}_{t-1}^{2}\,\frac{\partial {{\mathcal{C}}}_{t}}{\partial {{\boldsymbol{\sigma }}}_{t-1}}+ \frac{{{\boldsymbol{\sigma }}}_{t-1}}{N\,{{\boldsymbol{\sigma }}}_{\,\text{prior}\,}^{2}}\,({{\boldsymbol{\sigma }}}_{\,\text{prior}\,}^{2}-{{\boldsymbol{\sigma }}}_{t-1}^{2})\right],$$

(34)

We note that γ need not be fixed at 0.5 as in our continual-learning derivation—other interpretations (e.g., tempered posteriors44 or simple Newton steps) can alter its value.

Under Lemmas 1 and 2, we have \(\,\frac{1}{{{\boldsymbol{\sigma }}}_{L}^{2}}=\frac{N}{{\boldsymbol{\sigma }}}\frac{\partial {\mathcal{C}}}{\partial {\boldsymbol{\sigma }}}=N\,{H}_{D}({\boldsymbol{\mu }})\). Treating σ as a function of discrete time (iteration) t, we obtain a Bernoulli differential equation of the form

$${\boldsymbol{\sigma }}{\prime} (t)+ a(t)\,{\boldsymbol{\sigma }}(t)=b(t)\,{\boldsymbol{\sigma }}{(t)}^{n},$$

(35)

with n = 3, \(a(t)=-\frac{\gamma }{N}\), and \(b(t)=-\frac{\gamma }{N}(N{H}_{D}({{\boldsymbol{\mu }}}_{0})+\frac{1}{{{\boldsymbol{\sigma }}}_{\,\text{prior}\,}^{2}}).\) Solving this via Leibniz substitution yields:

Proposition 1: Consider the Bernoulli differential equation \(\sigma {\prime} (t)+a(t)\,\sigma (t)=b(t)\,\sigma {(t)}^{n}\) under \({\sigma }_{\,\text{prior}\,}^{2}\ge \sigma (0) > 0\), n = 3, \(a(t)=-\frac{\gamma }{N}\), and \(b(t)=-\frac{\gamma }{N}(N\,{H}_{D}({\mu }_{0})+\frac{1}{{\sigma }_{\,\text{prior}\,}^{2}})\). Its solution is:

$$\sigma (t)=\frac{{\sigma }_{0}\,{e}^{\frac{\gamma t}{N}}}{\sqrt{\,1+ N\,{\sigma }_{0}^{2}({H}_{D}({\mu }_{0})\,+\,1N\,{\sigma }_{\,\text{prior}\,}^{2})\,({e}^{2\gamma tN}-1)}},$$

where σ0 = σ(0).

From this closed-form, one sees that the convergence timescale \({t}_{c}=\frac{N}{\gamma }\) does not directly depend on σ0. As t → ∞,

$$\mathop{\lim }\limits_{t\to \infty }\,{\boldsymbol{\sigma }}{(t)}^{2}=\frac{1}{N}\frac{1}{\,{H}_{D}({{\boldsymbol{\mu }}}_{0})+ 1N\,{{\boldsymbol{\sigma }}}_{\,\text{prior}\,}^{2}}.$$

(36)

Thus, σ(t)2 becomes inversely proportional to the Hessian diagonal (plus a small residual term), aligning well with the intuition that σ encodes synapse importance.

In practice, mini-batches only approximate i.i.d. data, adding stochasticity to the curvature estimate \(\,\frac{1}{{\boldsymbol{\sigma }}}\,\frac{\partial {\mathcal{C}}}{\partial {\boldsymbol{\sigma }}}\).

Case  N → ∞

When N is infinite, forgetting disappears, and the update rule reduces to \(\,{\sigma }_{t+1}={\sigma }_{t}(1-\frac{{\sigma }_{t}^{2}}{2\,{\sigma }_{L}^{2}})\). Setting \({\alpha }_{t}=\frac{{\sigma }_{t}}{\sqrt{2}\,{\sigma }_{L}}\) yields the recurrence \(\,{\alpha }_{t+1}={\alpha }_{t}(1-{\alpha }_{t}^{2})\), which converges to zero but at a rate such that \(\,\mathop{\lim }\limits_{t\to \infty }{\alpha }_{t}\sqrt{2t}=1\) (the proof is available in Supplementary Note 3). Hence,

$$N=\infty \Rightarrow \mathop{\lim }\limits_{t\to \infty }t\,{\boldsymbol{\sigma }}{(t)}^{2}=\frac{1}{{H}_{D}({{\boldsymbol{\mu }}}_{0})}.$$

(37)

In this regime, σ(t)2 eventually collapses, reflecting overconfidence and vanishing plasticity—mirroring phenomena seen in FOO-VB Diagonal. By contrast, any finite N preserves a stable nonzero variance, maintaining EU and ensuring that crucial weights are not overconstrained. This highlights the need for a controlled forgetting mechanism in continual learning.

Uncertainty in neural networks

In our experiments, we measure both aleatoric and epistemic uncertainties following the approach of Smith and Gal25. They decompose the total uncertainty (TU) of a prediction into two parts: AU and EU. Formally, they use the mutual information between a model’s parameters ω and a label y conditioned on input x and dataset \({\mathcal{D}}\):

$${\mathcal{I}}({\boldsymbol{\omega }},y| {\mathcal{D}},x)=H[\,p(\,y| x,{\mathcal{D}})]-{{\mathbb{E}}}_{p({\boldsymbol{\omega }}| {\mathcal{D}})}\,H[\,p(\,y| x,{\boldsymbol{\omega }})],$$

(38)

$$\,\text{EU}\,=\,\text{TU}\,-\,\text{AU}\,.$$

(39)

Here, H is the Shannon entropy45, and \(p(y| x,{\mathcal{D}})\) is the predictive distribution obtained by averaging over Monte Carlo samples of ω from \(p({\boldsymbol{\omega }}| {\mathcal{D}})\). Concretely, one samples weights \({{\boldsymbol{\omega }}}_{i} \sim p({\boldsymbol{\omega }}| {\mathcal{D}})\) to compute p(y∣x, ωi), then averages these distributions over i.

In this framework, AU captures the irreducible noise in the data or measurement process, while EU reflects uncertainty about the model’s parameters. EU tends to decrease as the model gathers more evidence or restricts the effective memory window (as in MESU), thereby limiting overconfidence. This separation of uncertainties has been widely adopted in the literature11,23, allowing a more nuanced evaluation of model predictions and their reliability.

MNIST and Permuted MNIST studies (Figs. 3, 4)

We use the standard MNIST dataset26, consisting of 28 × 28 grayscale images. All images are standardized by subtracting the global mean and dividing by the global standard deviation. For Permuted MNIST, each image’s pixels are permuted in a fixed, unique manner to create multiple tasks.

Architecture

All networks displayed in Fig. 3 have 50 hidden rectified linear unit (ReLU) neurons, with 784 input neurons for the images and 10 output neurons for each class.

Training procedure

Supplementary Note 5 describes the steps of the training algorithm. Training was conducted with a single image per batch and a single epoch per task across the entire dataset. For Permuted MNIST (Fig. 3), accuracy on all permutations was recorded at each task trained upon. For MNIST (Fig. 4), accuracy was recorded after each epoch. Each algorithm was tested over five runs with varying random seeds to account for initialization randomness.

Neural network initialization

The neural network weights were initialized differently depending on the algorithm. For SGD, SI, Online EWC Online as well as EWC Stream, weights were initialized using Kaiming initialization. Specifically, for a layer l with input dimension nl and output dimension ml, the weights ωl were sampled according to:

$${\omega }_{i,l} \sim {\mathcal{U}}\left(-\frac{1}{\sqrt{{n}_{l}}},\frac{1}{\sqrt{{n}_{l}}}\right).$$

(40)

For MESU and FOO-VB Diagonal algorithms, mean parameters μi,l were initialized using a reweighted Kaiming initialization and σi,l were initialized as a constant value:

$${\mu }_{i,l} \sim {\mathcal{U}}\left(-\frac{4}{\sqrt{{n}_{l}}},\frac{4}{\sqrt{{n}_{l}}}\right),{\sigma }_{i,l}=\frac{2}{\sqrt{{n}_{l}}}.$$

(41)

For Bayesian models, the choice of initial variance strongly influences the posterior’s exploration range during the first few updates, and we therefore treated the initialization scale as a hyper-parameter. The parameters in Eq. (41) were obtained by grid search.

Algorithm parameters

Hyperparameters for SGD, EWC Online, and SI were obtained by doing a grid search to maximize accuracy on the first ten tasks of the 200-task Permuted MNIST. MESU uses Eqs. (10) and (11) directly, which have no learning rate: No tuning of the learning rate is performed (the same is true for FOO-VB Diagonal). For MESU, the memory window N was set to 300,000 to remember about five tasks of Permuted MNIST. The prior distribution for each synapse of MESU is set to \({\mathcal{N}}(0,0.06)\) for MNIST and \({\mathcal{N}}(0,1)\) Permuted MNIST. Table 1 lists the specific parameter values used for each algorithm considered.

Table 1 Hyper-parameter values for each algorithm of Figs. 3 and 4Model-width ablation

All protocols above were repeated with four network widths (50, 256, 512, 1024 hidden ReLU units) so as to disentangle the roles of capacity and memory window N. The full results, together with the corresponding uncertainty curves and variance histograms, are provided in Supplementary Note 6.

CIFAR studies (Fig. 5)

We use the standard CIFAR-10 dataset29, consisting of 32 × 32 RGB images. All images are normalized by dividing by 255. Our network comprises four convolutional layers followed by two fully connected layers with ReLU activations (see Table 2).

Table 2 CIFAR-10/100 model architecture and dropout parameters. m: number of tasksTraining procedure

In the single-split setting, we first train on CIFAR-10 (Task 1). We then sequentially train new tasks, each comprising ten classes of CIFAR-100 (which we follow consecutively). A multi-head strategy is used: each new task adds ten units (one “head”) to the final layer, and during training, the loss is computed only at the head corresponding to the current task. For testing, we use the head associated with the relevant task. Each task is trained for 60 epochs with a mini-batch size of 200, and dropout is applied (see Table 2).

When splits are introduced, each task from the single-split procedure is subdivided into splits (sub-tasks). The network first learns the initial split of each task in sequence, and this process is repeated for subsequent splits.

Neural network initialization

The neural network weights were initialized differently depending on the algorithm. For Adam, SI, and EWC weights were initialized using Kaiming initialization, as described in the previous section. For MESU, mean parameters μi,l were initialized using a reweighted Kaiming initialization, and σi,l were initialized as a constant value. Specifically, for a layer l with input dimension nl and output dimension ml:

$${\mu }_{i,l} \sim {\mathcal{U}}\left(-\frac{\sqrt{2}}{\sqrt{{n}_{l}}},\frac{\sqrt{2}}{\sqrt{{n}_{l}}}\right),{\sigma }_{i,l}=\frac{1}{2\sqrt{{m}_{l}}}.$$

(42)

As in the Permuted MNIST case, the parameters in Eq. (42) were obtained by grid search.

Algorithm parameters

To determine the best λ parameter for EWC, we performed the experiment with 1 split for different value, with 0.1 ≤ λ ≤ 10. Adam is the special case of EWC where λ = 0. To determine the best c parameter for SI, we performed the experiment with one split for different value, with 0.02 ≤ c ≤ 0.5. Furthermore, as in the original paper14, the optimizer is reset at each new task. We set αμ (for MESU) by choosing the smallest value that maximized test accuracy on the first CIFAR-10 task. Meanwhile, ασ (for MESU) was determined based on our theoretical analysis of standard-deviation dynamics in the i.i.d. scenario (see the related “Theoretical Results and Methods” sections). Specifically, as σ converges on a timescale \({t}_{c}=\frac{N}{{\alpha }_{\sigma }}\), we selected ασ so that by the end of training on the first task, at least two of these timescales had elapsed, ensuring that the standard deviations had sufficient time to converge. Table 3 lists the specific parameter values used for each algorithm considered.

Table 3 Hyper-parameter values for each algorithm of Fig. 5Animals-dataset studies (Fig. 2)

This study is based on a subset of the “Animals Detection Images Dataset” from Kaggle46. We used a ResNet18 model trained on ImageNet from PyTorch and removed its final fully connected layer to extract 512-dimensional feature vectors for each image. Training was conducted for five epochs per task with a batch size of one image. The neural network weights were initialized in the same way as in the CIFAR experiment. We then set the learning rates α (for SGD) and αμ, ασ (for MESU) following the same procedure described for the CIFAR experiment. Table 4 lists the specific parameters used for each algorithm.

Table 4 Hyper-parameter values for each algorithm of Fig. 2Architecture

All networks displayed in Fig. 2 have 64 hidden ReLU neurons, with 512 input neurons for the images and five output neurons for each class.