The retrospective analysis comprised 598 high-resolution oral photographs of consecutive patients diagnosed with OLK, accompanied by their corresponding clinical data. All patients were diagnosed clinically and histopathologically in accordance with the World Health Organization (WHO) criteria7,10, following a standardized protocol: (1) Clinical assessment to exclude other clinically recognizable white or white/red lesions. A provisional diagnosis of OLK is made when a white lesion or white/red lesion is observed on the oral mucosa that cannot be definitively diagnosed as another condition; (2) Biopsy of the lesion to exclude other pathologies that may present as white or white/red lesions. The histopathological findings associated with oral leukoplakia range from simple epithelial hyperplasia with hyperparakeratosis or hyperorthokeratosis to the presence or absence and degree of epithelial dysplasia. In addition, all patients diagnosed with OLK were explicitly advised to abstain from alcohol and tobacco use. Data were collected from the Hospital Authority Clinical Management System (HA-CMS) of Queen Mary Hospital and Prince Philip Dental Hospital, covering the period from January 2003 to December 2024 (follow-up endpoint). Sample inclusion criteria in dataset collection were defined by: (a) Both clinical and histopathological assessments were employed to confirm the OLK in all patients. (b) A minimum follow-up duration of 6 months was maintained for all patients. (c) The pathological results were reviewed and confirmed by two experienced specialists to ensure the accuracy of the diagnosis. Regarding the exclusion criteria, patients diagnosed with OLK alongside Head and neck squamous cell carcinoma (HNSCC) either before their initial visit or within 6 months after the first visit were excluded from the study. Additionally, cases with less than 6 months of follow-up and those diagnosed as proliferative verrucous leukoplakia (PVL) were also excluded.
This study adheres to both the Strengthening the Reporting of Observational Studies in Epidemiology (STROBE) reporting guideline and the Standards for Reporting of Diagnostic Accuracy (STARD) reporting guideline. This study was conducted in accordance with the principles outlined in the Declaration of Helsinki. Approval for this study was obtained from the Institutional Review Board of the University of Hong Kong/Hong Kong West Cluster (Reference number: UW23-094). To safeguard patient privacy and confidentiality, the researchers anonymized all clinical data, removing any potential identifiers before proceeding with data analysis.
The presence or absence of OED was assessed through histopathological examination by certified pathologists. Given the extended time span of our real-world data, OED classification followed three WHO systems: the 1978 system (mild/moderate/severe dysplasia), the 2005 system (hyperplasia/mild/moderate/severe dysplasia and carcinoma in situ), and the 2017 system (mild/moderate/severe dysplasia)31,32,33. To maintain fidelity to real-world clinical practice, including diagnostically ambiguous cases (e.g., mild-moderate or moderate-severe), we preserved original diagnostic classifications. Notably, hyperplasia cases were explicitly excluded from our dysplasia classification framework. This approach ensured that our AI-driven approach accurately reflected clinical decision-making patterns. To address datasets’ heterogeneity while retaining clinical relevance, we adopted a binary stratification system (Class I/II): Class I included mild, mild-moderate, and moderate cases, whereas Class II comprised moderate-severe, severe, and carcinoma in situ cases. The timing of the transformation of OLK to OSCC is defined as the interval between the biopsy date of the original OLK lesion and the first histological diagnosis of malignancy.
The following textual data were collected for each corresponding case: (1) Personal characteristics (age and gender, smoking habits, and alcohol consumption); (2) Clinical manifestations (clinical subtype, lesion location, diameter, and size); (3) Presence of OED at initial diagnosis or during follow-up, along with its grading; (4) Treatment options; and (5) Occurrence of malignant transformation (time-to-event). For discrete variables, label encoding is used to convert them into integer labels, thereby avoiding the high sparsity caused by one-hot encoding. Label encoding maps each value of a feature to a unique integer, transforming clinical text data into information that can be understood by the model.
$${{\rm{Label}}\; {\rm{Encoding}}}\!:{{\rm{c}}}_{{\rm{i}}}\left\{\begin{array}{cc}0 & {{\rm {Category}}}\,0\\ 1 & {{\rm {Category}}}\,1\\ \begin{array}{c}\vdots \\ n-1\end{array} & \begin{array}{c}\vdots \\ {{\rm {Category}}}\,n-1\end{array}\end{array}\right.$$
Here, \({{c}}_{{i}}\) represents the encoded value for the ith categorical feature, and n denotes the total number of categories for that feature.
High-resolution clinical images were obtained for each patient, effectively illustrating the OLK lesions. For the image processing phase, no regions of interest (ROIs) were defined. To address the inconsistent image dimensions in the original clinical photos, all input images were resized to a fixed spatial resolution prior to being fed into the neural network. Specifically, a uniform resizing operation was applied to standardize all images to 224 × 224 pixels, ensuring consistency in network input and enhancing the reliability of feature extraction during model training. Besides, data augmentation techniques were employed to expand the dataset artificially. This approach introduces minor variations or utilizes advanced methods to generate additional examples, enhancing the model’s efficiency. The applied data augmentation techniques include random vertical flip, random rotation, center crop, random affine transformation, gaussian blur, random noise addition, and color Jitter, all of which contribute to the model’s robustness and adaptability. Specific hyperparameter values are detailed in Supplemental Note 2.
In this study, we present OLK multi-modal multi-task prediction network (OMMT-PredNet), a customized end-to-end deep learning framework that achieves full automation for multitasks prediction. The fundamental principles and architectural foundations of the proposed system are as follows:
We designed a novel model architecture that combines ResNet50 with the convolutional block attention module (CBAM) (ResCBAM) to evaluate the presence of OED in clinical images of OLK. Description of model construction and deployment phases undergone in this study is shown in Fig. 3. ResNet50 is a deep convolutional neural network architecture comprising 50 layers, specifically engineered to overcome the challenges associated with training very deep networks. It consists of 48 convolutional layers, along with a MaxPooling layer and an Average Pooling layer, resulting in over 23 million trainable parameters. This complexity enables ResNet50 to capture intricate patterns present in the clinical images.
Fig. 3: Illustration depicts the architecture of the end-to-end automated multi-model framework OMMT-PredNet (OLK multi-modal multi-task prediction network) for multiple tasks.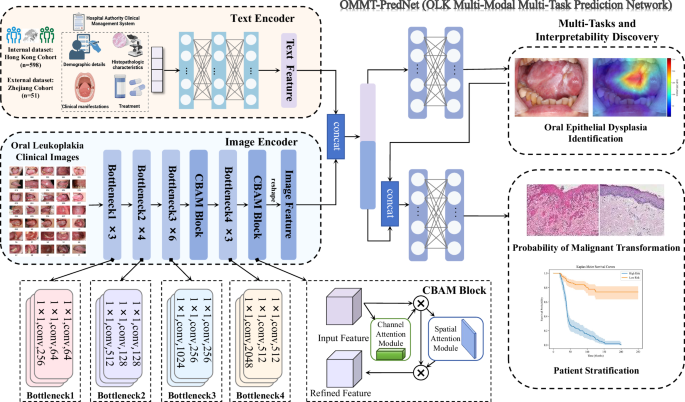
ResNet50 Residual Network 50, CBAM convolutional block attention module.
A key innovation of ResNet50 is the implementation of residual learning, which mitigates the issue of vanishing gradients commonly encountered in deep networks. The architecture employs skip connections that allow gradients to propagate through the network without degradation, facilitating the training of deeper models. The residual block can be mathematically expressed as Eq. (1):
$$R(x)={{\rm {Output}}}-{{\rm {Input}}}=H(x)-x$$
(1)
where x represents the input to the neural network block and \({H}({x})\) represents the true underlying function that the network aims to approximate. By rearranging this equation, we express the output as Eq. (2):
$${{\rm {Output}}}=H(x)+x$$
(2)
This formulation indicates that the residual block learns the residual mapping \(R(x)\) enabling the network to focus on learning the differences between the input and the desired output, thereby simplifying the learning process and enhancing generalization. A detailed explanation of model principles was described in Supplemental Note 3.
While ResNet50 demonstrates strong performance in various image classification tasks, it has limitations. One notable drawback is its inability to selectively focus on the most informative features within the feature maps, which can lead to suboptimal performance on datasets with high variability, such as those with OLK lesions that present OED. The model may struggle to distinguish between subtle differences in dysplastic changes due to the presence of noise and irrelevant information. Moreover, our model was trained without any manually annotated ROI. This presents a unique challenge, as the model must autonomously identify and assess relevant features across the entire image. In such scenarios, the lack of explicit guidance can further complicate the learning process. To address these limitations, we introduced CBAM after both layers 3 and 4 in the ResNet50 architecture. This attention mechanism enhances feature representation by adaptively refining channel-wise and spatial feature responses, effectively amplifying diagnostically relevant features while suppressing noise and less informative regions. This is particularly beneficial given the characteristics of our dataset, which includes images with varying degrees of dysplasia and noise. By incorporating CBAM, we enable the model to dynamically adjust its attention based on the importance of each feature and spatial region, thereby improving its classification performance even in the absence of manually defined ROIs.
CBAM operates as a lightweight attention mechanism designed to improve the representational capacity of convolutional neural networks. CBAM functions in two sequential stages: channel attention and spatial attention. A detailed explanation of model principles was described in Supplemental Note 4.
Channel attention module: This module computes attention scores for each channel, allowing the network to emphasize informative features while suppressing less relevant ones. The channel attention map is generated using global average pooling and global max pooling, followed by a shared feed-forward network, represented mathematically as Eq. (3):
$${M}_{{\rm {C}}}=\sigma ({{\rm {MLP}}}([{F}_{{{\rm {avg}}}},\,{F}_{\max }]))$$
(3)
where \({F}_{{{\rm {avg}}}}\) and \({F}_{\max }\) denote the pooled feature maps, and \(\sigma\) is the sigmoid activation function.
Spatial attention module: Following channel attention, the spatial attention module further refines the feature maps by focusing on pertinent spatial regions. It generates a spatial attention map using the output from the channel attention module, combining global average pooling and global max pooling across the channel dimension (Eq. (4)):
$${M}_{{\rm {s}}}=\sigma (f([{F}_{{{\rm {avg}}}}^{{\rm {c}}},\,{F}_{\max }^{{\rm {c}}}]))$$
(4)
where \(f\) is a convolutional operation that results in a 2D attention map.
The final output of the combined model is obtained by multiplying the original feature map with both the channel and spatial attention maps (Eq. (5)):
$${F}_{{\rm {refined}}}={M}_{{\rm {c}}}\odot ({M}_{{\rm {s}}}\odot F)$$
(5)
where \(F\) is the original feature map, and \({F}_{{{\rm {refined}}}}\) is the enhanced representation.
The architecture’s ability to automatically highlight essential features and regions significantly improves its performance in OED detection, thereby facilitating accurate diagnosis.
To analyze the relevant risk factors, we employed the textual feature encoder (TFE), which leverages multiple fully connected layers to capture complex interactions and higher-order abstractions. The architecture of the TFE is structured as follows:
Input layer: Accepts pre-processed clinical information.
Hidden layers: (a) lth Fully connected layer: Comprises N1 neurons with ReLU activation functions; (b) (l + 1)th fully connected layer: Consists of N2 neurons with ReLU activation functions. (c) Dropout layer: Applied after each fully connected layer to reduce overfitting by randomly deactivating a fraction of neurons during training. Mathematically, the transformation at each layer \(l\) can be expressed as Eq. (6):
$${h}^{(l)}={{\rm {ReLU}}}({W}^{(l)}{h}^{(l-1)}+{b}^{(l)})$$
(6)
where \({W}^{(l)}\) and \({b}^{(l)}\) are the weight matrix and bias vector for layer \(l\), respectively, and \({h}^{(l-1)}\) is the input from the previous layer.
Output layer: Generates the final encoded clinical feature vector FTextual. which serves as an input to subsequent stages of the multimodal model. The output layer may use a linear activation function or another suitable activation depending on the specific requirements of the model (Eq. (7)).
$${F}_{{{\rm {Textual}}}}={W}^{{{\rm {out}}}}+{h}^{(L)}+{b}^{{{\rm {out}}}}$$
(7)
where \(L\) denotes the final hidden layer.
The OLK image is processed by the ResCBAM image encoder module to obtain the feature representation \({{F}}_{{\rm{Image}}}\). The feature representation \({{F}}_{{\rm{Textual}}}\) is derived from the TFE module. Image features extracted via ResNet50 + CBAM are dimensionally aligned with clinical text embeddings. Subsequently, the image features and text features are fused through concatenation (concat). The combined feature representation \({F}\) is obtained through the following calculation (Eq. (8)):
$${F}={\rm{concat}}\left({{F}}_{{\rm{Image}}}\right.,\left.{{F}}_{{\rm{Textual}}}\right)$$
(8)
After feature fusion, we employed an OED-specific classifier to predict grades, followed by survival analysis incorporating multi-tasks. Our framework enables fully automated end-to-end training, where each module operates independently. Therefore, the final loss consists of three components: the OED classification loss, the MT prediction loss, and the survival loss, which together facilitate multi-task learning. Specifically, we utilize Cross Entropy Loss for the classification task, BCE With Logits Loss for scoring trajectories, and Cox proportional hazards loss for survival analysis. The details of losses are as follows:
OED classification loss: The cross-entropy loss is utilized for the classification of OED, defined as follows (Eq. (9)):
$${{\rm {Loss}}}(y,\hat{y})=-\mathop{\sum }\limits_{i=1}^{C}{y}_{i}\log ({\hat{y}}_{i})$$
(9)
where \({y}_{i}\) represents the true label, the \({\hat{y}}_{i}\) denotes the predicted probability for the positive class. This loss function has been implemented to optimize the model’s performance in the classification of OED.
MT prediction loss: For scoring trajectories, we utilize the BCE with logits loss, denoted as \({L}_{{{\rm {BCE}}}}\), which combines a Sigmoid layer and the binary cross-entropy loss in one single class. It is given by (Eqs. (10) and (11)):
$${{L}}_{{\rm{BCE}}}=-{y\cdot }\log ({\sigma }({x}))-(1-{y}){\cdot }\log (1-{\sigma }({x}))$$
(10)
$${\sigma }({x})=\frac{1}{1+{{\rm{e}}}^{-{x}}}$$
(11)
where \(y\) is the true label indicating the presence of MT, and \(x\) denotes the raw output (logits) from the model prior to applying the sigmoid function\(\sigma (x)\). This loss function is crucial for optimizing the model’s ability to accurately predict malignancy potential.
Survival loss: For survival analysis, we employ the Cox proportional hazards loss, which is designed to handle censored data effectively34. It is expressed as Eq. (12):
$$l(\theta ):=\sum _{i:{E}_{i}=1}({\hat{h}}_{\theta }({x}_{i})-\log \sum _{j\in R({T}_{i})}{{\rm {e}}}^{{\hat{h}}_{\theta }({x}_{j})})$$
(12)
\({\hat{h}}_{\theta }({x}_{i})\) represents the predicted hazard function for the ith subject, while \(R({T}_{i})\) denotes the cohort at risk at time \({T}_{i}\). The goal is to assess the malignancy potential by modeling the time-to-event data, allowing for the identification of factors influencing malignancy progression. The Cox-PH model’s ability to handle censorship and its reliance on hazard ratios provide valuable insights into malignancy potential over time, enabling better risk stratification and clinical decision-making.
Total loss (automatic weighted loss): Automatic weighted loss is a method for automatically determining the weights of individual loss functions in multi-task learning (MTL) models that involve multiple loss functions. The primary objective is to optimize the weight distribution among different tasks or loss functions in an automated manner, thereby enhancing the overall performance of the model without the need for manual weight adjustment. To effectively balance these tasks, we employ a multi-task learning approach, as demonstrated in Eq. (13)35,36.
$$L=\frac{1}{{\sigma }_{1}^{2}}{L}_{{{\rm {reg}}}}+\frac{1}{{\sigma }_{2}^{2}}{L}_{{{\rm {conf}}}}+\frac{1}{{\sigma }_{3}^{2}}{L}_{{{\rm {cls}}}}+\mathop{\sum }\limits_{i=1}^{3}\log ({\sigma }_{i}+1)$$
(13)
where \({\sigma }_{i}\), \(i\)∈ 1, 2, 3} are learnable loss weights. Through backpropagation of the model, continuously minimizing the total loss \(L\), the model is able to optimize the weight distribution of the neural network, thereby enhancing overall performance.
The patient cases were randomly divided into non-overlapping training (80%) and test (20%) sets, which were used to train the models and evaluate their performance. These sets were constructed at the patient case level, meaning that all slides corresponding to a given patient case were assigned exclusively to either the training or test set; slides from the same case were never included in both sets simultaneously. We conducted experiments for each disease model using a five-fold cross-validation approach, reassessing patient cases into non-overlapping training and testing cohorts five times. The model hyperparameters were tuned using only the training folds, while the model’s generalization capability was evaluated on the held-out test folds.
Additionally, for external validation of the intelligent model, we utilized a cohort of 51 clinical images and patients’ corresponding textual data from Zhejiang University School of Medicine (Baseline characteristics were shown in Supplemental Note 5). While the sample size was moderate, the dataset demonstrated strong representativeness with parameters well-aligned to our model input requirements, featuring a mean follow-up duration of 2.06 years (range: 0.59-6.41 years) based on contemporary diagnostic standards.
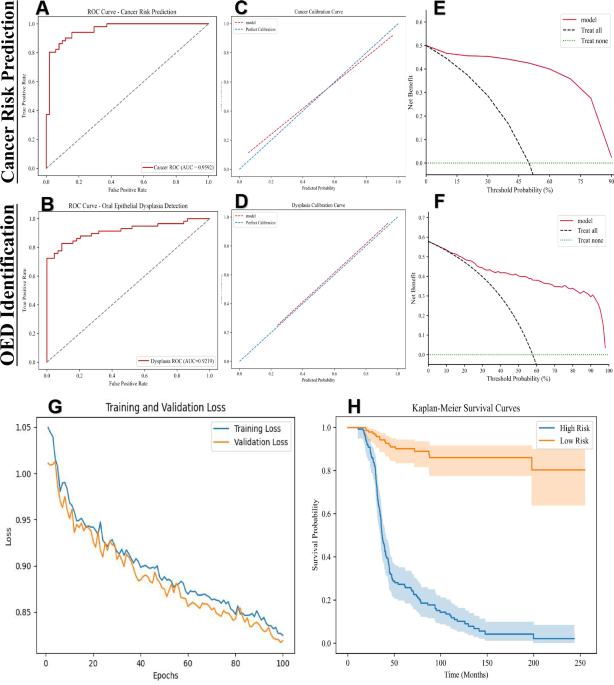
The performance of the cross-validated concordance index (c-Index) is reported as the average c-Index across the five folds. To estimate 95% confidence intervals during cross-validation, we utilized non-parametric bootstrapping with 1000 replicates on the out-of-sample predictions from the validation folds37,38. In addition to the c-Index, we also report the cumulative/dynamic AUC (referred to as Survival AUC), which is a time-dependent measure of model performance that evaluates the model’s ability to stratify patient risk at various time points, while also correcting for optimistic bias due to censoring through inverse probability of censoring weighting. To construct the Kaplan-Meier curves, we aggregated out-of-sample risk predictions from the validation folds and plotted them against survival time. The cutoff value was determined through ROC curve analysis on the validation set by calculating the Youden index for each potential threshold and selecting the value that maximized this metric. For assessing the statistical significance of patient stratification in the Kaplan–Meier analysis, we employed the log-rank test to determine whether the differences between two survival distributions were statistically significant (P-value < 0.05)39.
To assess the reliability of the model’s predicted probabilities, we performed calibration analysis using calibration curves, evaluating the agreement between predicted risks and observed outcomes. Clinical utility was further evaluated using DCA, quantifying the net benefit of the model across different threshold probabilities to inform its practical applicability in decision-making. Ablation studies were conducted to evaluate the contribution of the CBAM module by systematically comparing metrics with and without this component. Besides, a comprehensive set of metrics, including sensitivity, specificity, accuracy, precision, positive and negative predictive value, F1 scores, Brier score loss, and Youden’s J statistic, was evaluated. Mathematical calculations for the performance metrics are given below (Eqs. (14)–(20)):
$${\rm{Sensitivity}}=\frac{{\rm{TP}}}{{\rm{TP}}+{\rm{FN}}}$$
(14)
$${\rm{Specificity}}=\frac{{\rm{TN}}}{{\rm{TN}}+{\rm{FP}}}$$
(15)
$${\rm{Accuracy}}=\frac{{\rm{TP}}+{\rm{TN}}}{{\rm{TP}}+{\rm{FN}}+{\rm{TN}}+{\rm{FP}}}\,$$
(16)
$${\rm{Precision}}=\frac{{\rm{TP}}}{{\rm{TP}}+{\rm{FP}}}$$
(17)
$${{\rm{Positive}}\; {\rm{predictive}}\; {\rm{value}}}=\frac{{\rm{TP}}}{{\rm{TP}}+{\rm{FP}}}$$
(18)
$${{\rm{Negative}}\; {\rm{predictive}}\; {\rm{value}}}=\frac{{\rm{TN}}}{{\rm{TN}}+{\rm{FN}}}$$
(19)
$${F}1\,{\rm{score}}=2* \frac{{\rm{precision}}* {\rm{sensitivity}}}{{\rm{precision}}+{\rm{sensitivity}}}$$
(20)
All results were analyzed using Python version 3.10 (PyCharm 2023.2.8, Professional Edition, Wilmington, DE, USA).